0. おことわり
当雑記では,書籍『かけ算には順序があるのか』を批判する記述を多く入れています.
可能な限りそれぞれに根拠を書くよう努めていますが,いくつかの関連する書籍を読んだ上での判断というのが,背景にあります(書籍から学んだ,かけ算の順序をご覧ください).
加えて,この本の著者と思われる方が,かつて,当雑記のエントリにコメントを書かれたこと,またその内容も,一因となっています.
これらをご了承の上で,ご覧いただけると幸いです.
1. 本日の標題について
"Seeing is believing."のもじりです.
「百聞は一見にしかず」を英語に直すと「To see is to believe」でよ... - Yahoo!知恵袋もどうぞ.
2. 順列とみかんの個数 - 視覚的に

『かけ算には順序があるのか (岩波科学ライブラリー)』, p.18にある図です.
この図2だけを見て,「4個ずつ6人に配るから,4個×6=24個」と判断し,直前のページを見てなんじゃこら,なんでこれが樹形図になるんだ,なんて思う人がいるのでしょうかどうでしょうか.
…という発想,ナンセンスかどうかは判断しにくいところですが,思慮には欠けているとは思います.著者の言いたいことや,理解しておくべき前後関係を踏まえずに,目に飛び込んできたものだけを見ると,そんなふうに憤る人も,いるかもしれません.
実のところこの発想は,来年度の教科書―掛け算には「正しい順序」がある!? | メタメタの日と同型になっています.思慮の面,また前後関係は,どうでしょうか.自分の持つ偏見に基づき,文句を言っていないでしょうか.
3. 順列とみかんの個数 - 式から
たとえば,A,B,C,Dの4人が競争をした.1位,2位の決まり方は何通りあるか,という順列の問題では,4×3という式を書きます.1位の決まり方が4通りあって,そのそれぞれに2位の決まり方が3通りずつあると考えるわけで,樹形図をかくと,図1のようになります.この4×3の式は,「いくつ分(4)×1つ分(3)」という順序の式です.
「6人に4個ずつミカンを配る」という問題でも,6人に4個ずつ配られた状態を樹形図でイメージすれば,6×4という式のほうが「自然」に思えます(図2).
6人・4個という順で出てきた数を(わざわざ)4×6と逆にしなければならない,「1つ分の数」を先に書くのが(少なくとも)かけ算の導入期のルールなのだ,と言われても,交換法則を知っている大人にとっては,どうしても違和感が残るのは否めません.
(『かけ算には順序があるのか』, p.17)
場合の数の積の法則*1を使用することなく,言ってみれば小学生でも分かるような形で,理路を説明しているのは,分かるのですが,それでも,気になるものがあります.
式に単位が添えられていません.前に取り上げましたが,p.16の「トランプ式配り方」の式の解釈や,あとのpp.18-19では,単位付きの式が書かれています.別の言い方をすると,『「いくつ分(4)×1つ分(3)」』とありますが「いくつ分(4通り)×1つ分(3通り)」ではないのです.
素朴な立式だと,被乗数も乗数も積も,単位が同じになってしまう例として,今回のような,積の法則を利用した場合の数のほか,アレイ図(アレー図,ドット図とも)での数え方が該当します*2.読み進めると,p.27にその図があって,そこには『3個/列×5列』『5個/行×3行』*3をまず書いてから,単位を落として『…3×5と5×3では式の意味が違うということを…』と記しています.
1位2位の組み合わせを求める問題に関しては,1つ分を3通り/人,いくつ分を4人として「3通り/人×4人=12通り」とするほか,1位だけなら4通りで,2位を付け加えると1位は誰であっても3倍になることを図で確認した(そして倍概念に注意し,「倍」は単位とみなさない)上で,「4通り×3=12通り」といった式の立て方が思いつきますが,本文は「いくつ分×1つ分」が自然な一例として述べています.字数の制限があったのかもしれませんが,こういう話の進め方が,数学を豊かで味わいあるものにするようには,ちょっと思えません.
樹形図で考えることが分かりやすいかについては,次の項目で取り上げます.
4. 1位・2位の組み合わせの別解
ABCDの順列というと,かつて情報交換したなあ…0×3と3×0は違う コメントでしたか.
小学生でも,実行できそうな解き方をいくつか,考えてみます.「ACBDの4人で1位と2位の組み合わせ」を求めることを目的としますが,人数が多くなったり,何位までのところを変えたりしても,同様にして求められることを目指します.
まず思いつくのは,樹形図ではなく,「1位,2位の決まり方」をすべて書くことです.漏れなくダブりなく(おっとこれは大人の用語だ),箇条書きにすると,次の2パターンが思い浮かびます.
- パターン1
- 1位はA,2位はB
- 1位はA,2位はC
- 1位はA,2位はD
- 1位はB,2位はA
- 1位はB,2位はC
- 1位はB,2位はD
- 1位はC,2位はA
- 1位はC,2位はB
- 1位はC,2位はD
- 1位はD,2位はA
- 1位はD,2位はB
- 1位はD,2位はC
- 全部で12通り
- パターン2
- 1位はA,2位はA…これは除外
- 1位はA,2位はB
- 1位はA,2位はC
- 1位はA,2位はD
- 1位はB,2位はA
- 1位はB,2位はB…これは除外
- 1位はB,2位はC
- 1位はB,2位はD
- 1位はC,2位はA
- 1位はC,2位はB
- 1位はC,2位はC…これは除外
- 1位はC,2位はD
- 1位はD,2位はA
- 1位はD,2位はB
- 1位はD,2位はC
- 1位はD,2位はD…おれは除外.間違えた,これは除外
- 「除外」しなかったのは全部で12通り
かけ算を使わず,勘定することになります.100人になったら全部書けませんので,途中を「……」で省略し,「}」と数を添えたいところです.
こう書いた上で,樹形図との比較ですが,樹形図は書くべき文字数を減らすことができます.ある種の抽象化とも言えます.そして,1位のうちの1つに対して,2位が3つ,枝分かれしているという関係です.「1位がA,2位がBとCとD(3人がみな2位)」という読み方をする図ではありません.このような樹形図の読み方(そして書き方)は,児童が自然に思い浮かぶものではなく,(できれば簡潔性・拡張性を含め,教師か親か周りの者が)教えないといけない事柄であり,「社会的知識」の一つです.結局のところ,樹形図を活用した数え上げは,上記の「パターン1」「パターン2」を導かせたり,天下り的に教えたりするのとは,ちょっと異なる技能のように見えます.
ここだけ大人モードですが,n人の場合,パターン1ではn(n-1)通りとなるのに対し,パターン2ではn^2-n通りと表せ,因数分解してn(n-1)と等しいことを確認することになります.
解き方に戻りましょう.もう一つ方法があって,表にすることです.リーグ表みたいなものです.
HTMLで表を組み,スクリーンショットを撮りました.
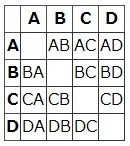
表頭(行見出し)・表側(列見出し)を除き,各行が1位,各列が2位の名前で,マスの「AB」は「1位はA,2位はB」の省略形です.1位と2位が同じ人ということはありませんので,そこは空白とします.英字2文字の組み合わせがいずれも異なることを確認してから,1位2位が書かれているマスの数を計算するには,
- どの列も3通りあるので,3通り/列×4列=12通り
- どの行も3通りあるので,3通り/行×4行=12通り
- 正方形の領域から対角線の成分を取り除くので,4×4-4=12 答え12通り
など,いろいろ思いつきます.
脱線して,「1位だけ」「1位・2位・3位の組み合わせ」「1位・2位・3位・4位の組み合わせ」を表にしてみました.

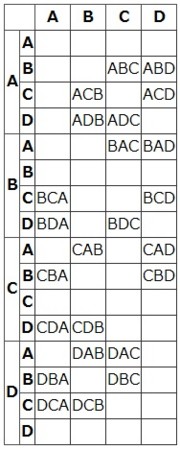
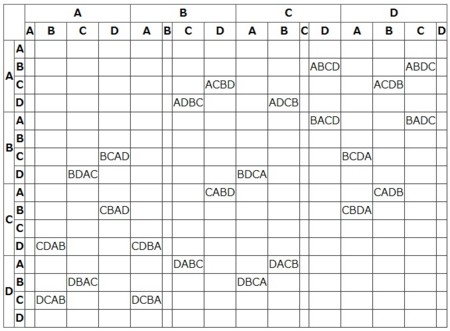
表全体を見れば規則性は分かると思いますが,3位までの場合,表側が2列になり,その外側(左の列の各文字)が1位,内側(その右の列の各文字)が2位,そして表頭(最上段の各文字)は3位を表します.3位まで,4位までの場合の数の計算に使えそうな式の候補が違っているのも,興味深いものです.
5. あらためて,乗法の意味について
算数では,a)同数累加の簡潔化やb)単位あたりのいくつ分の事象を低学年で扱い,それの応用として,c)長方形的配列(直積型)を用い,d)において乗数が有理数の場合も扱う.長方形の面積の公式は,c)の特殊な事象として見いだすことができる.しかし長方形の求積公式は「量と測定」の内容であり,「数と計算」の内容とは区別して扱う.
(「教員志望学生の算数における乗数の意味の拡張のとらえ方について」*4, p.2)
現代化当時,文部省でわが国の学習指導要領の作成のまとめを行っていた中島は,わが国の教科書の扱いについて,乗法を加法の特別な場合を簡潔に表すという立場から意味づけることは,低学年の場合は教育的にも意味があり,この立場をとっている.しかし累加の考えの問題点は,乗数が有理数の場合に起こる.そこでわが国では,累加という考えをそのまま用いないで,次のような意味に一般化する方法がとられた.
Aを基準(単位)とする大きさとし,BをAを単位とした測定数とするとき,A×BはBの目盛りに対応する大きさを読み取ることにあたる.
(図:省略)
これは,割合ともいわれているが,A×BはAという単位量のスカラー倍を表すという考えである.この場合,乗数が整数の場合に累加の考えを特別な場合として含んでおり,整数,小数,分数に関係なく一貫して用いられ,また小数,分数の乗法が適用される場合をこの意味に基づいて一般的に理解させ,乗法の適用判断を統一的に能率よく行うことができる.このような考えに基づいた扱いが現在においても継続されており,数学的な考えの育成という観点からも指導法が検討されている.
(同上,p.3)
乗法の意味に関する先行研究の多くは指導法についてなされている。指導の時期に照らし合わせると導入時に行われる乗法の意味づけの指導、九九の構成活動における意味を深める指導がある。従来の指導を考察することで指導の目標とする乗法の意味理解の視点が見えてくる。第1に乗法の必要性である。(略)整数の乗法の範囲では、比例的な見方の素地を作ってくことが重要であると考える。児童にとっての必要性は簡便性になる。繰り返して加えるより、簡単に処理するために乗法的操作を用いようとするところにある。第2に乗法の定義である。整数の乗法を単位が決まったときに、その単位を基にして、それを繰り返し加えて全体の数量を求めるための計算方法や表現方法とする。例えば、文章題の場面で、四則計算のどれにあてはまるかと考える場合にそこから単位(1つ分の大きさ)にあたる数といくつ分にあたる繰り返しの数を読みとり乗法で立式ができることである。この定義については導入時に学習する。(略)いずれにしても、被乗数と乗数にあたる数の意味が異なることを理解させる必要がある。第3に乗法の性質である。2年生の段階では、乗法の答えが累加で求められること、全体の数は乗数が1増えると被乗数分増えるということ、交換法則などがある。
整数の乗法の理解過程に関する研究(PDF)
2. 乗法の意味
(1) 数学的な立場から
数学はできるだけ少数の基礎的概念を基にして新しい概念を構成するという立場をとるから,乗法は加法を基にして,同数累加として定義される.すなわち,乗法は次の2つの式で一般に定義される.
(i) a×1=a
(ii) a×(b+1)=a×b+a
すなわち,aに1をかけるとはa自身のことであると定義し,a×2, a×3, ……は,2,3,…の定義と(ii)を用いて
a×2=a×(1+1)=a×1+a=a+a
a×3=a×(2+1)=a×2+a=(a+a)+a
……………
のように,順次同数累加として定義される.これは既知の加法を基にして,乗法を定義する立場であるから,数学的には正しいが,算数指導では,このような論理的立場をとるのではなく,子どもの経験世界を基にするので,このような立場をとるわけにはいかない.第一,×1を最初に定義するようなことは,子どもの心理や乗法の必要性から考えて,子どもには受け入れ難いことである.
(内海庄三: 「整数の乗除」の意味と計算指導のキーポイント, 整数の計算 (リーディングス 新しい算数研究), p.121)
かけ算の意味については,次のような場合が考えられる。
乗法の意味についてのメモ | メタメタの日
(1)数×数
(2)量×数
(3)量×量
(以下,同日夜に追加)
ヴェルニョー(Vergnaud, G.)は,乗法・除法を成立させている最も基本的な操作や場面を,2つの量空間の間の比例関係から捉えようとする.乗法は,導入に際しては同数累加の簡便法として意味付けられることが多いが,ここではヴェルニョーの考え方と図式を利用して乗法の意味を捉えてみる.
(1) スカラー関係に基づく乗法
(図:省略)
この図式における乗法の意味は,量空間M1において1に対するbの割合からb倍(スカラー倍)を抽象し(倍概念),それをM2の量aへ適用する見方である.例えば,M1を針金の長さ,M2を重さとし,「1mが200g (a)の針金の2.5m (b)分の重さ(x)を求める」場面は,この見方に基づくと,「2.5mは1mの2.5倍だから,求める重さ(x)も200gの2.5倍である」と意味付けられる.一般的な言葉の式では,
(求める全体量:x)=(基準量:a)×(倍量:b)
となり,bを単位を持たない割合とみると比の第二用法になる.
(2) 関数関係に基づく乗法
(略)
(3) 量の積に基づく乗法
(略)
(『算数・数学科重要用語300の基礎知識』, p.187)
「積 (×)」はつぎのように定義されます:
量qをm倍し,さらにこれをn倍したら,もとのqの何倍になっているか?
この倍を,「m×n」と書くことにする。
(以上,同日夜に追加)
どれがいい/間違い/好き/嫌いではなく,数学上・数学教育上のこれまでの(多くは論文・書籍の)検討に基づき,各著者の見解を表明しているものとして,並べてみました.
乗法の意味について書かれているものを本気で収集し分類すると,ずいぶんな量になりそうに思えます.またしばらくの間,ブックマークやネタメモに入れて,数がたまったらリリースするとします.
6. 球形,じゃなくて休憩
「じょうほう」と打ち込み,ときには「情報」,ときには「乗法」と変換させていると,誤変換のままリリースすることになりやすくて,困りました.
そこで辞書登録を行い,「じょうはう」から「乗法」に変換するようにしました.快適になりました.
まあ,歴史的かなづかいとしては「じょうはふ」らしいのですが.
7. 5×3を推す人
今日のリンクでは「立式の論理と計算の便宜 (3×5≠5×3問題)」のひとが3×5ではなく5×3があるべき姿であるという主張をしていて、はからずも、順序を決めるなんて本質的に無理なことなんだと示しているようで興味深かったです。
『かけ算には順序があるのか』を読んだ コメント
何の話かというと
のことで,まず,内容自体の個人的意見は次のとおり.
- 《別解》により,「1つ分の大きさ」を5,「いくつ分」を3と書くことができます.
《別解》ですが,「しき」として書いた「5×3=15」と,それまでの授業の仕方・問題の解かせ方からは,そのような考え方にはならず,問題文にある5と3を取り出し,単純にかけ算としたと読み取られています.書いた内容から何を考えたかが伝わらなかったので,バツとなったということです.
「×」から学んだこと
ミカンを配るのに,トランプを配るときのやり方で配ると,1回分が6こ,これを4回くばるのだから,それを思い浮かべる子どもは,むしろ,
6×4=24
という方式をたてるほうが合理的だといえる.その式が思い浮かぶのと,それを答案に書いて思い浮かんだ意図どおりに採点者(先生)に理解されるのは,別のことです.マルをもらい,自分も安心,先生も安心できて,より高いステップに進むためには,式をどう立てるにとどまらず,その式で伝わるかを考えていきたいものです.それが,文章題で式を答えさせることの意義です.
2冊 - わさっき
6月11日追記:図にすることに関しては,過去の誤記に目を閉ざす者はにて「状況をdouble-tree structureにする」を書いています.追記ここまで.
そして興味深いのは,追記として書かれている,以下の記述です.
b)
5×3を推す (3×5≠5×3問題)
問題文の筆者が、「さらが5まいあります。」を先に書いたのって、「引っ掛け問題」のつもりだったのかもしれないな。
記事を書き始めて数分後にその可能性に思い至り、脱力して半月くらい放り出していた。冒頭に「さらが5まいあります。」を配置した問題文が「引っ掛け問題」として成立しうるのは、「日本語の制約からくる先入観に基づく誤読が、逆に正当な読みとされる状況だから」だ。
この推測に対しては,現在,そして過去に,どのような形で,かけ算の文章題が出題されてきたかを調査し,分類すればいいだけのことです.
当雑記では,ちょうどコメントを寄せていただいたエントリで,「交換法則を学べばどちらでもよい」の中に4問,挙げています.分類の一例はAB型とBA型で,「BA型」で当雑記を検索すると,他の事例を知ることができます.
といったことをもとに,以下のように書いたのでした.
ごんべえさんの書かれている2番目の段落に関しては,「問題集に目を通す」ことで(略)ある程度解決できると見ています.
『かけ算には順序があるのか』を読んだ コメント
8. なぜ問題集?
ネットの議論よりも,問題集を読むことをおすすめする意義を,大学での教育研究の活動を踏まえて,説明します.
担当授業の中で,「安全なシステムを考案する人は,自他で提案したシステムの安全性を検証する人でもある」とスライドに書き,学生に見せています.
口頭で説明する際には,合わせて,「これを,工学上の問題解決全体に対して成り立つよう,拡張することができます.つまり,より良いモノを考案する人は,自他で提案したモノが本当により良いモノなのかを検証する人でもあるのです」と言うようにしています.
かけ算をめぐる論争でいうと,モノはもちろん,出題(文章題のインスタンス)となるでしょう.そして,誰かが提示したモノ=出題だけを見て,その良否を判定してはいけないのです.
良否を言うためには,まず,その出題がなされる背景を押さえておきます.解答者は何を知っていて,その出題に答えることになるまで,どのような出題を(授業あるいはドリルで)見て学習してきたかを,可能な限り,知りたいところです.リアルタイムで監視というわけにはいきませんので,ある程度の推測,そして誤差が含まれるのは,仕方がありません.
次の段階は,見てきた問題のグループ分けです.そしてグループ単位で,どういう意図なのか,最終的にどのようにして問題が解けるようになればいいのか,言ってみれば「解法」を推定します.なお,「解法」には,立式・計算の方法を含みますが,それらに限定されません.かけ算の文章題でいうと,「何が『一つ分の大きさ』,何が『いくつ分』になるかを読み取ること」そして「その問題はかけ算を使って答えられる,と判断すること」が指摘できます*5.
世の中でどういった出題がなされているかを知るのはもちろん,事前事後の学習者の能力(「〜できる」という形であらわされるもの)を手っ取り早く知るには,出題における前提条件がよく分からないネット上の議論よりも,算数以外に課題をお持ちでお忙しい現場の先生に尋ねるよりも,入門にと話題の本を買ってその背景にあるマイナーな考えに陥ってしまうよりも,まずは問題集を何冊か買って読むことを,推奨する次第です.
9. 「教育はデザイン」とは?
これまでちょくちょく,「デザイン」という言葉を取り入れています.
ここのあとがきから,著者は小学校における「かけ算・わり算」指導の課題をよく見据えた上で,この本そしてシリーズで何を解決しようとしているのか,児童らには何をどのように習得してほしいのか,また指導する側にはどのように学ばせるとよいかが,配列・例示されているのだなと,理解できました.そしてここでも,教育や指導というのはデザインなのだということを思い起こさせます.
1993年の「かけ算とわり算」指導法
ここから2つのことが知ることができて,まず,「何のいくつ分」によるかけ算の立式が,児童たちには徹底しているということでしょう.そして,図の,花の配置と枠囲みが,「4×8」という式を立てさせるのをひどく不自然にしています.「ひどく不自然」というのは否定表現ではなく,先生の側で意図的にデザインしたものだと,理解しています.
山梨のケース,新潟のケース
これらから,良い教育のためには良いデザインが必要だというのは,言ってよさそうです.(略)
形成的評価について
少々古いのだと,技術のエッセンスは,設計も教育に関係しますし,デザインについて,書いたこととして雑記内リンク集を作りっています.
「デザイン」を,この言葉を使わずに説明すると,次のようになります.
「一つの問題に対して,複数の解決法があるとき,どれを選んで,形にするか?」
自分を支えるものは何か,考えてみた
そしてこれは,文章題を解くときだけでなく,教育について語るときにも役立ちそうです.指示を与え児童に問題を解かせる先生なり,子どもを見る(ただし授業参観を除き,直接授業の状態を見ることのできない)親御さんが,それぞれの制約のもとで,どのように行動して,ときにはマル,ときにはバツ…改善しよう,となるのかを考える際の基本原則として,使うのです.
かけ算の順序---さっさとこの問題設定から脱却したいのですが---に対して,適用すると,こうなります.乗法の交換法則が成立する範囲を,何を対象とするのかについて,いくつか候補が考えられます.『「1あたり量×いくら分」でも「いくら分×1あたり量」でもどっちでもいい』という考え方も,候補の一つです.次に,各候補の得失を明らかにします.そして,さまざまな要因,社会の要請・閣議決定(ゆとり・脱ゆとりなど)などをもとに,結論を下します.
これまで見知った出題例・指導例をもとにすると,現状,小学校教育で選択されているのは,
- 一つ分の大きさを被乗数,幾つ分(もしくは何倍か)を乗数
- 基準にする大きさを被乗数,割合を乗数
として式で表すこと*6であり,そこにおいて被乗数と乗数を逆に書くことは認められていないのです.
少ない書籍や論文を読んで想起できる,膨大な数学教育の蓄積からは,樹形図や,領収書の書式,m times n(『かけ算には順序があるのか』, p.45)といった少数・軽微な事例が,今後,変化を与えるようには到底思えません.
*1:例えば,http://www.shinko-keirin.co.jp/j-kadaimath/0605/, http://www.cfv21.com/math/casenum.htm
*3:「個/列」「列」「個/行」「行」といった単位表記が大人モードであり,アレイ図をもとに児童にそのように書かせたり発見させたりするのは,面倒な作業のように思えます.
*4:http://ci.nii.ac.jp/naid/110004614978にアクセスし,「CiNii 論文PDF - オープンアクセス」をクリックすれば,PDFファイルが取得できます.
*5:これらの点まで踏まえて小学校の教育の難しさ・面白さを伝えようとしている,(学術的でない)書籍の筆頭は,やはり『田中博史の算数授業のつくり方 (プレミアム講座ライブ)』です.
*6:適切な式で表されたあと,計算して結果となる数を求めることは,また別の操作であり,そこには,交換法則・結合法則・分配法則などを見ることができます.なお,日常生活に見られるものやすでに学んだことを起点として計算に有用な性質を学習するのであって,「量の交換法則」を含め,その逆は必ずしも成り立たないこと---これもまた選択の結果---には,注意が必要です.