いきなりですが問題です.
T 42×3を,筆算で計算しましょう.(黒板に書く.)C1さん,こっちに来て,書いてくれますか.
C1 はい.3×2=6(さんにがろく)なので,一の位は6です.繰り上がりはありません.3×4=12(さんしじゅうに)なので,十の位は2,百の位は1です.答えは126です.
T みなさん,このように書けましたか?
C2 先生,質問です!
T C2さん,どうしたの?
C2 2×3=6(にさんがろく),4×3=12(しさんじゅうに)じゃないの!?
さっそくですが元ネタです.
- 先に3と2をかけて6,次に40と3をかけて120だけど,12とかく.下から上にかけます.
- 3の段のかけ算で答えが出てくる.上からやると2の段と4の段のかけ算になってしまうね.しっかり覚えておこうね.
(『整数の計算 (リーディングス 新しい算数研究)』 p.176; 横山秀寿「3年:かけ算(2)」,新しい算数研究 1983年11月号(No.152), pp.45-50.)
「40と3をかけて」と書かれていますが,矢印と,「3の段の…」の説明から,そこは「3×4=12(さんしじゅうに)」で算出することになります.
C2さんの疑問を,大人モードで表すと,こうです:分配法則を使って42×3=40×3+2×3=120+6=126*1になるのだけれど,なぜ「4×3」「2×3」ではなく,「3×2」「3×4」とするのでしょうか.
回答するなら,「かける数・かけられる数がいろいろ変わっても,計算しやすく,混乱(間違え)にくくするため」というのが良さそうです.
- 筆算ではかける数なのに,内部計算の九九だとかけられる数にしているのは,その段の九九だけで答えを出せばよいからです.
- 下の位からかけていき,足していくのは,繰り上がりがあるような筆算に対処しやすいからです.
もちろん,そのように順序を変えてもいい数学的な背景には,乗法・加法の交換法則があります.
全体の計算と,その中の部分的な計算で,被乗数・乗数が逆になる書き方は,英語文献にも見られます.
10. It is possible to perform calculation such as 384 × 673 mentally by rehearsing the subtotals. For example, one can calculate 3 × 384 = 1152 and repeat "1152" mentally until it becomes a "chunk" which only occupies one short-term memory buffer. "Chunking" is a well-documented mechanism by which people can perform mental tasks.
(Handbook of International Research in Mathematics Education p.514; Alan H. Shoenfield: Research methods in (mathematics) education)
この中で,「3 × 384」がどこから出てくるのかというと,計算したいかけ算のかける数,673の一の位が「3」で,かけられる数「384」が,かける数になっています.ただし「筆算」とは書いていません.
ちなみに「10.」というのは,その記事のNOTESの10番目でして,本文でこの番号をつけているのはp.483です.そこでは,"The Magic Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information"*2が引き合いに出され,だけども384×673なんていう,3桁の数どうしのかけ算で,9つのsubtotalなんて覚えられない(普通,暗算できないでしょ),と持っていっています.
筆算の順序というか手順のバリエーションについては,片野善一郎「数学史からみた整数のかけ算・わり算」,新しい算数研究 1980年7月号(No.112), pp.7-10(『整数の計算 (リーディングス 新しい算数研究)』 pp.166-169)に詳しく記されています.当雑記でこの点についての疑問を持つようになったのは,ごく最近でして,数学と教育の協同をご覧ください.
ここに昨日の『「小学算術」の研究』が加わります.緑表紙教科書の編纂に携わった高木佐加枝が,かけ算の筆算について,次のように“かけ方”を述べています.
(略)これすなわち交換の法則である。したがって,筆算の掛算では一般に乗数先唱の九九を用いるのが便利である。
また,次のような場合には被乗数先唱の九九を用いればよいので,場合々々に応じて便利なように九九を活用すればよい.
(p.247)
もう少し前には,制限九九のときと,総九九とで,筆算でのかける方向…総九九の良さを示すために…も記されています.なお,原文では,2つの筆算は横並びです.
先の引用に「乗数先唱」「被乗数先唱」とありました.これらと関連語を,確認しておきます(不安な人は『かけ算には順序があるのか (岩波科学ライブラリー)』第二章も合わせてどうぞ).
- 乗数先書:乗数が先,被乗数が後の書き方
- 被乗数先書:被乗数が先,乗数が後の書き方
- 乗数先唱:乗数が先,被乗数が後の言い方
- 被乗数先唱:被乗数が先,乗数が後の言い方
「乗数先書・被乗数先書」については,2012年に「×」から学んだこと((2) 海外の順序,日本式の順序)で整理しています.ただしどうやら,この言葉のペアは[銀林1975a]以外には見られず,銀林の造語ではないかと考えています.
とはいえ,「乗数先書・被乗数先書」の違いを認識した上でないと,「乗数先唱・被乗数先唱」の違いも認識しにくいのです.すなわち,『「小學算術」の研究』の乗法の意味づけや指導法においては,被乗数先書が大前提であるように見えるのです.
より具体的に書くと,「被乗数先書 & 乗数先唱」と「被乗数先書 & 被乗数先唱」とを比較すれば,後者のほうが良いのだ,そして緑表紙でもその方針を採用したのだ,ということです*3.根拠になるものを,引用します.
a. 各段の九九を被乗数を一定にして纏めることにすると,この一定な数を冒頭に呼ぶ方が都合がよい。筆算の掛算では,乗数先唱を本体とするが,これは後に指導することで,九九構成の最初においては,被乗数先唱で九九を覚えさせることが,児童心理に叶っている。
b. 国語は,「5円の色紙を8枚」「3を4倍する」というように,被乗数を先にする言い方である.
c. 式に表す場合も 5円×8 というように,被乗数を先に書くのを常とするから,被乗数先唱の方が都合がよい。
(pp.246-247.一部改行を詰めた)
その本の展開としては,九九は被乗数先唱で覚えさせ,その後は「被乗数からでも乗数からでも,いずれから先に唱えても差支えないように指導する」とあります.続いて,例として3行4列のアレイを提示し,縦並びに着目すると3×4=12,横並びに着目すると4×3=12,「甲乙はないのでどちらでもよいのである。これすなわち交換の法則である」として,上述の筆算の“かけ方”につながっていきます。
現在の算数指導もまた,「被乗数先書 & 被乗数先唱」です.もちろんそれらの言葉は,授業において(おそらく教師用指導書などにも)見られません.「2×30g=60g」や「テーブルの数×4=人数」*4といった,基準量や1あたり量が乗数になるように見える形でも,数量関係の知見を取り入れれば,「30」や「4」のほうが,かける数です.
九九の学習において,乗数先唱の概念は「昔はね…」です.筆算も乗数先唱ではなく,全体としてはかけられる数・かける数の役割を,内部計算では逆にし,効率良く処理していくわけです.
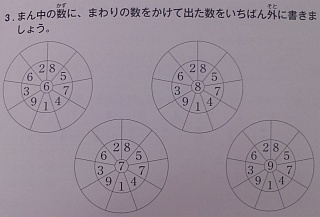
ここで最後に,図をお見せします.
他の本でも,目にしたことがあります.
この問題を最初に見たときは,百ます計算の対抗くらいに思っていました.
しかし,筆算を念頭に置くと,また別の意義が浮かんできます.これは,中軸になる数を「かけられる数」,その外にある数を「かける数」として,いろいろな方向に「かける」ことができるようになってほしい,という出題意図になっています.筆算の素地指導なのです.
*1:これに対応する分解式すなわち「40×3=120 2×3=6 120+6=126」が,p.175で反応の一つとして書かれています.
*2:wikipedia:ジョージ・ミラー,http://www.mendeley.com/research/the-magic-number-seven-plus-or-minus-two-some-limits-on-our-capacity-for-processing-information/
*3:なお,黒表紙あるいはそれ以前において,「乗数先書」と「被乗数先書」との比較が行われていたのかどうかは,分かっていません.