乗数が内包量

かける数が1あたりでは，いわゆる1あたり量（内包量）が乗数に来るような乗法について，1980年代に書かれたVergnaudの解説*1を根拠としていました．
1970年代の，遠山・銀林の著書にないかな…と大学図書館に立ち寄って，探してみると，あっさり見つかりました．

こうすれば算数数学がわかる―人間行動からみた数学教育

この中の「第9講　式にも単位がある」(pp.128-144)です．話としては中学の数学で，ある文章題から連立方程式を立てています．式の一つ，35x＋50y＝4450の両辺に14をかけて490x＋700y＝62300を得るとき，この「14をかける」というのが実は「14g/円をかけている」ことなのだと指摘しています．そしてp.142には，「乗数14g/円の意味」と題する節も設けられています．
その章（講）の最後のところに，《参考》として，『量の世界―構造主義的分析 (1975年) (教育文庫〈8〉)』の145ページを挙げています．そこはかつて読んだはず…と見直して，違いに気づきました．
銀林の『量の世界』も，Vergnaudも，「量の次元を変える関数」（『こうすれば算数数学がわかる』p.142）を指摘しているという点では同じです．
何が違うのかというと，結局のところ，表記です．『量の世界』p.146に見られるのは，次のとおりで：


Vergnaudのほうは，こう書かれています(p.130)：

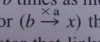
「密度ρ」「発熱量m」「速度v」の左に「×」がついているか，Vergnaudの書いた関係の中で「×a」が「a×」になっているかしていたら，自分の「かける数が1あたり」に対する認識も，また異なっていたわけなのですが．

*1:Vergnaud, G.: Multiplicative Structures, Acquisition of mathematics concepts and processes, Academic Press, pp.127-174 (1983). 英語文献の取得や読解に不安のある方は，『算数・数学科重要用語300の基礎知識』のp.187をご覧ください．