1. ここがデタラメ 「かけ算の正しい順序」
この全文,そしてそのブログの各記事を見まして,「かけ算の順序」を持ち出して批判する人々が,次にどんな行動をするだろうかと,考えました.
思いついたのは次の3つです.
- 海外展開
- コンテンツの管理,配布の円滑化
- 続刊
それぞれ,もう少し詳しく説明します.教科書を通じた日本の算数教育への批判は,じきに限界に達し,「海外展開」になるだろうなと,想像したのでした.ある人々は洋書(英語に限らず)を紹介しはじめ,別の人々は「かけ算の順序」の問題点を英訳し,海外に向けて情報発信していく,という次第です.このトピックに関する英語のブログやフォーラムも,開設されるかもしれません.
「コンテンツ」とは,教科書や書籍・資料などです.現状,出典を記せば,使い放題な面があります.引用・転載のルールをその人々の間で取り決め,また自作の図表についてはクリエイティブ・コモンズ(CC)・ライセンスなどを示すようにして,再利用を促すとともに,重要な課題の発見者,問題解決の立役者を,リスペクトする流れができないかと思っています.
「続刊」は,『かけ算には順序があるのか』に続くものです.
自分はというと,手持ちの本を見直すとともに,買い足して読んでいき,文献どうしの照合を,マイペースにやっていきます.海外や過去と比較した上で,日本の算数はどうあるのか,これからどうなっていくといいかを,もう少し明瞭に,していきたいところです.コンテンツについては,これまで作ってきたいくつかの絵について,CCをつけていきますか….
ところで,冒頭の記事にリンクしたのは,「かけ算の順序」に対する批判の象徴的なものであるのに加えて,『『マンガ嫌韓流』のここがデタラメ―まじめな反論 不毛な「嫌韓」「反日」に終止符を!対話と協力で平和を!!』の本を思い出したからでした.
2. 高木貞治,そして量
対話する気なし.ま,いいや.学習者にスイッチし,書誌情報・関連情報を見直しました.
- 足立恒雄: 高木貞治に見る数学思想の変遷, 数学通信, 日本数学会, Vol.15, No.2, pp.6-27 (2010). http://mathsoc.jp/publication/tushin/1502/1502adachi.pdf
- 日本数学会・高木貞治50年祭記念市民講演会
- はてなブックマーク - 高木貞治に見る数学思想の変遷
この文章で,主要な役割を演じているのは,「量」です.
さて,洋の東西を問わず…というのは言い過ぎなので,我々がアクセス可能な範囲で,先達が「量」をどのように認識してきたかについては,「見取図」が作られています(倉賀野1984, p.27).

もちろんこの図が完成形,ではありません.実際,この図では高木貞治の名前が見当たりませんが,おそらく著者は,現在なら文庫本で入手可能な『新式算術講義』をはじめ,高木の著書にアクセスできなかったのでしょう(南雲道夫の論文には,高木の著作が参考文献に入っていますが).
「量」と算数・数学教育の中で,もう一つ思い浮かぶのは,Vergnaudの文献です.「a×b=x」の構造を示す,2種類の図です(Vergnaud 1983, p.130).

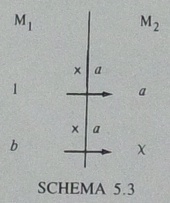
その前のページには,"two measure-spaces M1 and M2"と書かれています.measure-spaceは「量空間」と訳すのがよく,中原2000, p.187においても,この語が使われています*1.
図の前後の本文を,直訳ではなく自分なりに解きほぐしていくことにします.以前にも少し書きましたが,今回はその詳細版です.
まず,「1個15セントのケーキを4個買います.いくらになりますか」という問題を考えます.aを15セント,bを4個とします.xは60セントであって,60個ではありませんね.SCHEMA 5.2, 同5.3とも,M1はケーキの個数の量空間,M2は金額の量空間です.
SCHEMA 5.2の考え方では,M1で1個から4個になるのを「×b」とします.同じ量空間における「b倍」を,M2へ適用することで,a=15セントの「4倍」がx=60セントになるわけです.
このとき,「×b」のbは,もはや「4個」ではありません.あえて量という言葉を使うなら,無次元量です.
SCHEMA 5.3は,横に見る関係といえます*2.1個だと15セント,という関係を「×a」で表します.そうすると,4個だと,「×15」とするので60セントです.
ちょっと注意したいのは,この場面での「×15」は,数だけ見れば15倍ですが,実際には,M1という量空間からM2という量空間へ変換しています.あるいは,「×a」が,M1とM2という2つの異なる量空間の仲立ちをしている,と考えることもできます.
このとき,「×a」のaは,これまた「15セント」ではなく,「15セント/個」とするほうが,より適切でしょう.言葉にすると,「1個(あたり)15セント」です.
量空間は,数学的に定義しているわけではなく,同じ性質の集まりという程度なのでしょう.その一方で,数学的な取り扱いでの「量」だと,連続量が対象とせざるを得ないところ,Vergnaudの議論では,ケーキの数や金額など,分離量も視野に入れています.
何に依拠するにしても,一長一短があるといったところで.
(最終更新:2013-01-18 朝)
*1:同一の図(というか表)もあります.Vergnaudの別文献をもとにしていますが,算数・数学学習におけるわり算に関する研究, p.9でも,同様の関係を見ることができます.
*2:比例を含む2つの数量の関係は,2行任意列の表を作るのが一般的です.その際,行ごとに同じ種類の情報,すなわち同じ量空間の要素を書きます.そうすると,「縦に見る関係」として,考えることができます.