算数教育・資料集（書籍：2012年〜）

目次

• 小学校算数科授業の基礎技術Ｑ＆Ａ
• 先生のための学校　計算力が確実に伸びる指導
• 算数授業研究 第80号
• 田中博史の算数授業１・２・３年
• 小学校算数板書とノートを変えると子どもが伸びる
• 算数の教え方には法則がある
• 親子で学ぶ数学図鑑
• 理系への数学2012年5月号
• 算数教科書の用語・記号教え方ガイドブック
• 小二教育技術 2012年11月号
• 算数のつまずきには法則がある
• 数とは何か？
• アイディアシートでうまくいく！算数科問題解決授業スタンダード

小学校算数科授業の基礎技術Ｑ＆Ａ

プロ教師に学ぶ 小学校算数科授業の基礎技術Q&A

■教師の「簡単」と子どもの「簡単」は違う
授業で、ある問題の解き方がいくつか出されました。そこで教師は「一番簡単なのは、どれですか」という問いかけをしました。教師は「効率的」というような意味で「簡単」という言葉を使い、かけ算を用いた解法に目を向けさせるのが意図でした。しかしある子どもが、「僕は、たし算を繰り返して足していくほうが簡単だ」と言って譲りません。この子どもは「簡単」という言葉を「自分にとっての計算のしやすさ」といった意味でとらえていました。「簡単」という言葉は、算数では「効率的」という意味合いが強くなりますが、子どもはそのようにとらえるわけではないので、教師が困惑したり、納得させようと説明したりしてしまうことがあります。このような状況を避けるために、「式の数が少なかったり、計算する回数が少なかったりする式を『簡単な式』と考えます。皆さんが考えた中で『簡単な式』はどれですか」と問いかけることも有効です。同じ言葉でも、教師と子どものとらえ方が違う場合があることに留意して、発問することが大切です。
(p.93)

(p.94)

■式は事柄を表す
黙って、黒板に上のように書きます。そして「何でしょう」と問いかけます。子どもたちは、自信満々で手を上げ「十二です」と答えます。少し間をとった後「違います!」ときっぱり言うと、どの学級でも「えーー」という声が響きます。しばらくすると、「かけ算」「二十六」「二と六」などと答えます。
一通り子どもたちの考えを聞いた後、「式は答えを出すだけのものではありません。この教室の中にあるものを表しています。何を表しているのかわかったら、先生のところに来て、小さな声で教えてください」と説明・指示をします。
(p.95)

先生のための学校　計算力が確実に伸びる指導

先生のための学校 計算力が確実に伸びる指導 (教育技術MOOK 先生のための学校)

助数詞をつけると理解しやすい

式　2こ×3さら分＝6こ
式　3こ×2さら分＝6こ

これらの答えは6個と同じですが、式にすると全く逆です。
具体的なイメージをつかみにくい場合でも、助数詞（単位）をつける立式の間違いはほとんどなくなります。
このことによって、もとにする量×いくつ分がかけ算だということを理解させることができます。
また、三年生のわり算の学習で、等分除と包含除の違いがわかりやすくなりますし、小数や分数の文章題を習うときにも、この助数詞があることによって、立式の間違いを防ぐことができます。

(pp.22-23)

算数授業研究 第80号

算数授業研究 VOL.80

（p.11．磯田正美「我々は，何を，なぜ，いかに教えるか」）

「1mが120円のりごん2.7mのねだんはいくらか」(略)
このかけ算を2.7×120と書く子どもがいたらどうしようか。「なぜ，そう書いたのか」と聞くことになるだろう。その子が「もし1mのねだんが1円なら，2.7mのねだんは2.7円でしょう。でも，1mが120円だから，その120倍になる」と答えたら，これは素晴らしい。幸か不幸かまだ，そういう子どもに出会ったことはない。大切なことは，その式を支えているイメージを伴っているかどうかである。
（p.53．正木孝昌「かけ算のイメージを育てたい」）

田中博史の算数授業１・２・３年

田中博史の算数授業1・2・3年 (算数授業研究特別号)

本当にかけ算の表現がわかるかどうかを試すため，次のようないじわるな文章も入っている。

2こで1パックのプリンと，5こで1パックのプリンを1パックずつかいました。

「1パック」「ずつ」というような表現があると，かけ算だとすぐに考えてしまう子どももいて，これで2×5とする子がいる。
でもこの文章を絵にすると，次のようになる。
（図省略）
そうである。
単純なたし算の問題なのである。
(p.38)

先ほどの文章題カルタとは，目的を別にした九九専用のカルタも作ってみた。
こちらは『ビジュアル九九カルタ』（文溪堂）という。
かけ算の文章表現と式表現の約束を理解させることと，九九を覚えること，九九表の中の数のきまりを発見することなど九九全体の学習を目的としているので，こちらのほうはすべての九九をカードにすることが必要になる。カードは読み札が下のようになっており，絵札が別に付いている。

(p.38)

★

小学校算数 板書とノートを変えると子どもが伸びる

小学校算数 板書とノートを変えると子どもが伸びる

(p.31)

教科書問題場面は絵で示されている。
そこで，問題場面の1つぶんの数といくつ分とを把握しやすくするために，人をブロック（半具体物）で表し，以下の手順で板書する。

1. 問題分を板書し，さし絵を黒板に貼る。（さし絵は，人の絵をブロックに置き換えた後はがす。）
2. のりものが3台あることを確認し，3台分の枠を板書する。
3. 1台目ののりものに乗っている人を，板書上で児童と一緒に，一人ずつブロックに置き換え，6人乗っていることをおさえる。
4. 2台目，3台目も，3と同様にして，6人乗っていることをおさえる。
5. どののりものにも6人ずつ乗っていることを，のりものごとにブロックを数えてその上に6と板書し，「1台に6人ずつ，3台分あり，18人いること」をおさえる。
6. ブロック図で確認した「1台に6人ずつ3台文で18人」を児童に唱えさせ，ブロック図の下に板書する。

(p.32．箇条書きの番号は原文では丸囲み数字．2〜5の説明文の直後の図は省略した．)

3年 計算のしかたを考えよう(11/13時)
・本時は「かけ算はかける順番を入れ替えても答えは同じ」であることを学ぶ時間なので，問い方を工夫して一つの式にすることは正しいかを考えさせていく。

問題　1こ60円のおかしが1はこに4つ入っています。このはこを2つ買うと，代金はいくらですか。

まとめ　3つのかずのかけ算では，はじめの2つの数を先に計算しても，あとの2つの数を先に計算しても答えは同じになる。
（60×4）×2＝60×（4×2）

・4×2×60は問題場面に合わないので取り上げず，イのように8は4×2である確認から，60×（4×2）にもっていくようにする。
(p.50．ページ内の主要部のみ)

算数の教え方には法則がある

算数の教え方には法則がある

(2) 子どもが作る文章問題のほとんどは，出てくる数字の順序で計算する
(略)
だから，次のようなかけ算問題には混乱が生まれる。
「ベンチが5こあります。そこに6人ずつすわっています。ベンチにすわっている人は何人でしょう」
問題をつくったA男は，数字の順序で5×6としてしまった。
そこで「絵」を描かせると，「ああそうか」とA男は6×5の式が立てられた。
（図省略）
(p.71)

親子で学ぶ数学図鑑

親子で学ぶ数学図鑑:基礎からわかるビジュアルガイド

(p.19)

(p.29)

★

理系への数学2012年5月号

理系への数学 2012年 05月号 [雑誌]

(p.88．京都大学創作サークル「名称未定」（作画:フーフー&あむせ）：「ますまて」)

★

算数教科書の用語・記号教え方ガイドブック

若手教師必携! 算数教科書の用語・記号教え方ガイドブック

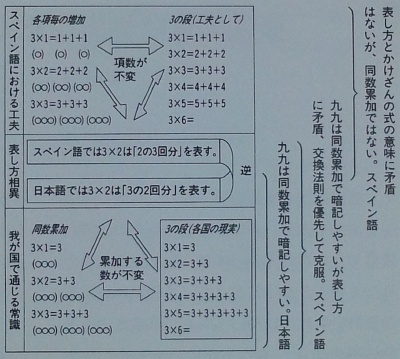
×は，乗法（かけ算）の操作を表す計算記号である。×は1631年にイギリスのオートレッドの本の中で使われた。彼の本には「乗法を美しくするために2つの数をinまたは×で結ぶ」と書いてあるそうだ。
乗法（かけ算）は，元来は3＋3＋3＋3のように同じ数を次々とたしていくことを簡単にすることから始まった。これを同数累加という。現在ではもう一歩前進して，1つ分の大きさが決まっているときに，そのいくつ分かに当たる大きさを求める場合に用いられるのがかけ算である。基準量のいくつ分ともいう。
3＋4と3×4では，同じ数字ではあるが意味が異なる。3＋4の場合だと3こ＋4こ，3cm＋4cmなのに対して，3×4の場合は，4こ×4つ分，3cm×4つ分とおなる。
(p.24)

小二教育技術 2012年11月号

小二教育技術 2012年 11月号 [雑誌]

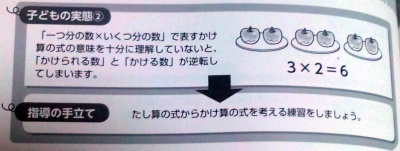
子どもの実態②
「一つ分の数×いくつ分の数」で表すかけ算の式の意味を十分に理解していないと、「かけられる数」と「かける数」が逆転してしまいます。
↓
指導の手立て
たし算の式からかけ算の式を考える練習をしましょう。
(p.55)

子どもの実態⑥
かけ算の文章題で立式をする際に、数値を問題文に出てくる順に式をつくっています。「一つ分の数」と「いくつ分」の数値が逆転してしまいます。
【もんだい】
３まいの　おさらに　４こずつ　りんごを　おきました。りんごは、ぜんぶで　何こでしょう。しきも　書きましょう。
しき　3×4＝12　答え12こ
↓
指導の手立て
「一つ分の数」が後から出てくる文章題で、練習をしましょう。
(p.59)

★

算数のつまずきには法則がある

算数のつまずきには法則がある クラス全員クリアできる,驚異のスモールステップ指導法

「かけ算」という言葉を学習した後，絵を見て，かけ算の式をつくるという学習場面である。
（東京書籍2下p.7／啓林館2下p.20／学校図書2下p.10／教育出版2下p.6／大日本図書2下p.20／日本文教出版2下p.8）

上記のような絵をかけ算の式にするところで，つまずく子がいる。
2×5と式を書けなければならないのだが，5×2などとしてしまうのだ。
これは，「1つ分」「いくつ分」などの言葉が定着していないことが原因である。
(p.50)

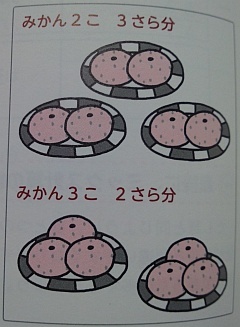
2個ずつが5皿分。
かけ算の式を教科書に書き込みなさい。

作業させた後に，教師が大事なことをもう一度繰り返す。これによって，子どもたちは式が書きやすくなる。この繰り返しをしていくしかない。
(p.51)

★

数とは何か？

数とは何か?―1、2、3から無限まで、数を考える13章 (BERET SCIENCE)

どのお皿にもミカンが3個のっています。お皿は全部で4皿あります。ミカンを集めて大きな袋に入れると、全部でいくつになるか？

これを次のように表す。
3個/皿×4皿＝12個
あるいは、
4皿×3個/皿＝12個
(略)
少しやさしい言葉でいえば、
（1当たり量）×（いくつ分）＝（全体量）
または、
（いくつ分）×（1当たり量）＝（全体量）
となる。
(pp.42-44)

■ かけ算の順序
「どのお皿にもミカンが3個のっています。お皿は全部で4皿あります。ミカンを集めて大きな袋に入れると、全部でいくつになるか？」という問題の答えを
3個/皿×4皿＝12個
という順序で表さなくてはいけない、と思い込んでいる人が多い。
4×3＝12　だから、12個
とか、
4皿×3個/皿＝12個
と書くと間違っていると思う人がいるというのだから困ったものである。
1皿当たり3個のミカンがのっていて、そのような皿が4皿あるのだから、4皿×3個/皿＝12個と考えるのは自然な発想なのである。この自然な、ある意味では合理的な思考を無理にやめさせようという考えは無理が生じるのである。
「かけ算の順序」について、「（1当たり量）×（いくつ分）」にしなければならないかを、子どもたちにいかに教えたかという小学校教師の奮闘記が新聞で紹介されたことがあるが、そんな先生の苦労を解放してやらなければならない。
「意味のないこと」「無駄なこと」「間違ったこと」を一生懸命教える先生がいなくなることを願うばかりである。
(pp.46-47)

★

アイディアシートでうまくいく！算数科問題解決授業スタンダード

アイディアシートでうまくいく! 算数科問題解決授業スタンダード

③ STEP1 「あれ?」を生む問題

3まいのおさらにりんごが6こずつのっています。りんごはぜんぶで何こですか。

④ 意味が欠落した手続き

（最初に出てきた数）×（後から出てきた数）

「あれ? どっちの式でもいいのかな」
⑤ STEP2 「なるほど!」を引き出す手だて

• 何のまとまりがいくつあるのかを明確にするために，文章に書かれている「りんごが6こずつ」と「3まいのおさら」と累加の式を板書で結び付ける。
• もし3×6だったらどんな問題になるかを考えさせる。
• 順序にこだわる子どもには，問題の「3まいのおさら」と「りんごが6こずつ」の言葉を入れ替えると式が変わってしまうことを確認する。

「なるほど! お話に出てくる数字の順番ではなく，お話と合った式をつくらないとだめなんだね」
(p.53)

もし
　3×6だとしたら
　6まいのおさらに
　りんごが3こずつ
　のっています。
になる!
(p.55)

★

（最終更新：2013-02-21 早朝）