「かけ算はかける順番が変わっても,答えは変わらない」という主張を,改めて考えてみることにします.
3に5をかけると,3×5=15です.5に3をかけると,5×3=15です.3×5=5×3は,乗法の交換法則を表した式となります.
別の「順番」もあります.2×3×4をどのように計算すればいいかです.まず,2×3=6,6×4=24とすることができます.あるいは,3×4=12としたあと,2×12=24となります.これは(2×3)×4=2×(3×4)と表現することができ,結合法則と呼ばれます.
いまの(日本の)小学校の算数では,交換法則・結合法則の式表現,乗法に限ると
交換法則:□×△=△×□
結合法則:□×(△×○)=(□×△)×○
は,第4学年で「四則に関して成り立つ性質」として,まとめることとなっています.ただし学習指導要領とその解説を読むと,交換法則・結合法則はそれよりも前にも現れます.第2学年では,加法に関して成り立つ交換法則や結合法則を学習します.また乗法の交換法則は「乗数と被乗数を交換しても積は同じになる」として第2学年で学習することとなっています.乗法の結合法則は第3学年です.
結合法則の図示,というのは,交換法則の図示ほど簡単でないように見えます.例えば『新編算数科教育研究』pp.39-40では,ペアノの公理系に基づく乗法の定義のところでは,結合法則,分配法則,交換法則が「演繹的に証明される」と書かれているのに対し,直積に基づく集合論的な立場では,アレイ図を提示し,「交換法則が成り立つこともあきらか」「分配法則が成り立つことも証明できる」とあるものの,結合法則への言及はありません.
交換法則は2つの値(または文字)を使った関係なので,長方形の面積で表せます.分離量だと,タイルの枚数です.結合法則は,3つの値または文字を使った関係なので,立体にしましょう.キューブの個数を算出します.
『Help Your Kids With Maths』には,次の図があります(p.161).
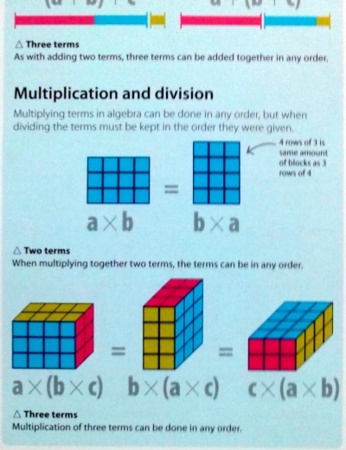
縦・横・高さの値が異なる一つの直方体を回転させることで,a×(b×c),b×(a×b),c×(a×b)のいずれの式でも,キューブの総数を計算でき,どれも等しいことを表しています.
他の本を見ます.Anghileri&Johnson (1988)のFIGURE 6-23 (p.179)は,The Associateive Propertyを示すための図として,次のように描かれています.
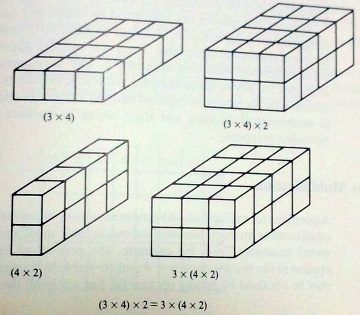
しかし,この図には,引っかかりを覚えます.というのも,かけられる数とかける数の区別が曖昧なように見えるのです.
この図をもとに,自分なりに3×(4×2)を作図してみました.

「3×4×2」の直方体では,式にカッコすなわち計算の順序を,入れないことにしました.
その一方で,「3×(4×2)」の式に対応する構成では,3次元という枠を外しました.3個の横並びの立方体を「一つ分」とみなして,それが4×2(縦4つ,横2つ)の長方形の配列として,表してみた次第です.
細かいことをいうと,「3×(4×2)」として表した図は,「3×(2×4)」と読むこともできます.長方形は縦横の,直方体は縦横高さの,実質的な区別がないと見れば,これは致し方ありません.
それと,Anghileri&Johnson (1988)の図のあとの練習問題(p.180)では,結合法則を使って計算を効率良くする出題が2問あります.その2番目「5×17×2」のヒントには「(Hint: use the commutative property as well.)」として,交換法則も使いなさいと書いています.概念としては別だけれど,交換法則と結合法則を合わせて,「計算の順序」に関する性質であることを,補強している事例となっています.
ここで,交換法則と結合法則を合わせたものが,「計算の順序」に関する性質である,と認識することにしましょう.複素数の範囲までで,加法と乗法はそれぞれ,計算の順序を変えても答え(和,積)は同じになります.減法と除法では異なってくるので,それらでは,計算の順序を変えられない,と言うこともできます.
高木貞治が1904年に著し,我々は文庫本で読むことのできる『新式算術講義 (ちくま学芸文庫)』には,「加法及乗法は組み合はせの法則及交換の法則に遵ふが故に,多くの数を加へ又は乗ずるに当りて,其順序を如何様に変更するとも結果は常に同一なり」と記されています(p.31)*1.このうち「組み合はせの法則」とは,結合法則のことです.
小学校で,乗法の結合法則をどのように学習しているかですが,3年で直方体の体積を扱えません*2ので,別の道具立てが必要となります.
以下に紹介する2つの事例はともに,お金の問題にしています.合計金額を算出するのに,2通りの方法をとって,どちらでも同じ答えを得る,という流れです.
まずはWebで読めるものから.第3学年 算数科学習指導案(平成18年10月24日,調布市立杉森小学校)では,「1こ90円のシュークリームが、1はこに3こずつ入っています。2はこ買うと、代金は何円になるでしょう?」を,今日の問題としています.
シュークリームの数を求めてから,全部の代金を求めるのが,3×2=6,90×6=540で,これを90×(3×2)=540と表すことができます.1箱の代金を求めてから,全部の代金を求めることにすれば,90×3=270,270×2=540となり,これは(90×3)×2=540です.
そうして90×(3×2)=(90×3)×2を導き,「かけ算はかける順番がかわっても、答えは変わらない」とまとめています.
自力解決の段階で,「90×2=180,180×3=540」という式も,予想される児童の反応として書かれています.しかしこれには「机間指導する」ともあり,この授業では,間違いとみなしています.
もう一つは,書籍からです.『小学校算数 板書とノートを変えると子どもが伸びる』p.50に書かれている授業では,「1こ60円のおかしが1はこに4つ入っています。このはこを2つ買うと,代金はいくらですか」という問題を提示しています.目指すのは「(60×4)×2=60×(4×2)」です.そのプロセスの中で,「4×2×60は問題場面に合わない」としています.
これら2つは,3年生の,乗法の結合法則を学習するための授業であるとともに,交換法則(□×△=△×□)を使用しないということでも共通しています.交換法則の考え方を排除し,「1つ分の大きさ×いくつ分=全体の大きさ」を用いて,□×(△×○)=(□×△)×○の一例を得ることができた,と言うこともできます.数学的にも,『新式算術講義』では分配法則を証明してから,結合法則・交換法則を別々に証明していることと重なります.
本日の記事は,かけ算の順序,計算の順序のうち,結合法則・交換法則に関するものを取り出した内容となっています.再構成を図ったのは,次のツイートを見かけたからです.
ここに[twitter:@sankunanaku]さんのお名前を書いて,リプライを送ることにします*3.
(最終更新:2013-04-24 深夜)
以下のとおり,大きな変更をしています(大意は変わりません).
- 脚注で,Perlほか,プログラミング言語を対象とした文字列のかけ算(繰り返し)を書いていたのは取り除きました.もう一つのブログで,Perl,Python,Rubyで「"3"かける5」を公開しました.
- 「交換法則と結合法則を合わせたもの」や,『新式算術講義』の言及(2つの段落)は,結合法則の図示のあとに移動させ,いくつか表現を修正しました.
最初のバージョンは,ウェブ魚拓よりご覧ください.
*1:これは0を含む自然数を対象としたもので,無理数(実数)を対象とした乗法の交換法則・結合法則は,同書p.284で示されています.その際,比例式γ:α=β:1を満たすγを,α,βの積として定義しています.
*2:単位正方形の個数によって長方形・正方形の面積を求めるということですら,第4学年の学習事項です.
*3:ブラウザで当該ツイートを見ると,自己参照の形で2つのツイートを見ることもできます.合併と増加が違う件は,途中で引用した『新編算数科教育研究』では他の演算についても,減法は「残り」と「ちがい」,乗法は「倍」と「積」,除法は「等分除」と「包含除」と大別し,四則計算の意味を表にしています.足し算の結合律の話は,1960年代の米国のかけ算に関する論争を紹介しながら,中島健三が記した「結論として,こどもは,具体的な経験をもち,それを一般的化していくのであって,最初の学年水準での一般化は,必ずしも,数学者の論理性に合致する必要はない」が関係するように思います.