本から:12人分のたな
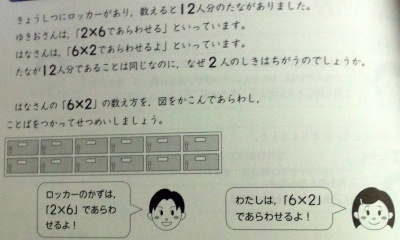
きょうしつにロッカーがあり,数えると12人分のたながありました。
ゆきおさんは,「2×6であらわせる」といっています。
はなさんは,「6×2であらわせるよ」といっています。
たなが12人分であることは同じなのに,なぜ2人のしきはちがうのでしょうか。
はなさんの「6×2」の数え方を,図をかこんであらわし,ことばをつかってせつめいしましょう。
元ネタは,以下の本のp.54です.
[isbn:9784491029870:detail]
といったところで【ゆきおさんのあらわしたしき】です.

ゆきおさんは,ロッカーの縦2つ分を基にして,「2つが6組」と考えています。だから,式で表すと,「2×6」となります.
すぐ下には【はなさんのあらわしたしき】の欄が見えます.囲い込みなしのロッカーと,【図であらわすと(図を○でかこみましょう)】【はなさんのしきのせつめい】もありますが,答案は作ってくださいねとなっています.
次のページには赤字で解答例が記されており,ロッカーの横6つ分を基にしています.
この出題には,見逃すわけにいかない重要な特徴があります.それは,結果となる答え(総数)を求めるものではない点です.総数はこの例だと「12(人分の棚)」で,問題文の最初の行に提示されています.結果ではなく,過程あるいは理由を答えさせる問題,と言うこともできます.
この種の問題を解くことが,「思考力・表現力」を評価する,もしくは培うものになるという意図だというのを,うかがい知ることもできます.本の副題の「B問題」は,全国学力テストの算数を念頭に置いてあります.当該テストを受ける,6年生になるより前*1から,学年ごとの学習事項に基づいた出題・学習ができることを,提案しているように感じました.
ところで,2×6と6×2のかけ算の件ですが,読んだ人によっては,ヒントの与えすぎに見えるかもしれません.【はなさんのしきのせつめい】を書く際には,ゆきおさんの2と6をそれぞれ6と2に置き換えて,転記すればいいだけじゃないか,と文句をつけることもできます.こんな出題で,「かけ算の意味」が分かったと言っていいのか,育成できるのか…
個人的には,これは「かけ算の意味」を2年生の子どもたちが理解するための教材例だと思っています.となると,「かけ算の意味」として何を学んでほしいかを,きちんと整理することが,大事になります.そして答案として何を書くか,あるいは何をアウトプットできてほしいかは,理解を見るための手段です.整理した項目と,子どもたちの関心を基に,適切な出題を作って与え,解かせてフィードバックを得るのが,教師の務めとなるわけです*2.
上記の本は今年になって入手しました*3が,2013年には他にも,文章→式→答えという求め方が古いのだ,子どもたちに取り組んで問題はこれだ,とでもいうような本を見る機会がありました.『アイディアシートでうまくいく! 算数科問題解決授業スタンダード』(*)と『算数の学習プリント―学力調査・算数的リテラシーに対応! (教育技術MOOK)』(*)を挙げておきます.
ツイートから:「直積」に関しては
昨日の,当ブログのログを見ると,不自然なURLによるアクセスが見られました.
http://t.co/wYwFDaHFSTがhttp://d.hatena.ne.jp/takehikom/searchdiary?word=%c4%be%c0%d1に展開されます.t.coのほうのURLを検索すると,ツイートも発見できました.
読んでほしいという意図は,承知できますが,http://d.hatena.ne.jp/takehikom/searchdiary?word=%c4%be%c0%d1というURLは,決して良いものではありません.というのも,これは「当ブログの最新から5件,『直積』を含む記事」を求めることとなり,現在は,この記事が筆頭となるからです.当ブログで今後,記事の中に「直積」を書いたら,それが最新となるわけで…そのURLに対応する情報の中身(コンテンツ)が,変わってしまうのです.*4
もう少しツイートを読ませてもらうと,[twitter:@tetragon1]さんと[twitter:@LimgTW]さんとで,やりとりを重ねているようです.
これまでに書いた記事の中から,「直積」を検索しても容易に見つからない,関連情報をピックアップしておきます.参考になりましたら幸いです.まず分類については,1段落でまとめたものがあります.
国内外の文献で,かけ算の分類法をいろいろな人が提案している.その中でも,かけ算を「倍」に由来するものと「積」に由来するものに大別するのが分かりやすい.「倍」は,かけられる数とかけ算の答えが同種の量であり,かける数は単位または助数詞があっても,割合あるいは拡大率とみなして,演算時に無次元となるようなかけ算をいう.「積」は2つの純粋な数どうしのかけ算と,2つの量をかけてそれらと異なる量を得るかけ算からなる.2つに大別した上で,より細かな分類が[Greer 1992]で表になっている.もし3つに分けるのなら,「倍概念」「比例関数」「複比例」が知られている[森1973][Vergnaud 1983].4つだと,「累加」を加えるとよい[田中2008].
3.3 「倍」と「積」のかけ算
このうち「複比例」は,2つの因数が連続的なものを対象としていますが,これを離散的なものにすると,「直積」となります.また「「累加」を加えるとよい」というのは,そこで引用した文献[田中2008]*5では「正比例型(一あたり量×いくつ分=全体量),直積型(面積),倍比率型(倍),累加型(たとえば3+3+3)の4通り」(pp.155-156)と例示しています.「一あたり量」など,数教協ベースの意味づけに加えて,「累加」にも(重要度を低くする書き方ですが)言及しています.「累加」をどのように活用すべきかについては,[Vergnaud 1983]と[Vergnaud 1988]を読み比べた際にも,見えてくるものがありました.
メタメタさんの記事のほか,かけ算の意味あるいはかけ算が使われる場面の分類については,「×」から学んだこと 14.02でリンクしています.
直積はどのような数学的また算数・数学教育的な背景にあるのかについて知るには,以下の文献がおすすめです.CiNiiでは有料ダウンロードとなります.主要部はここからどうぞ.
- 中島健三: 乗法の意味についての論争と問題点についての考察, 日本数学教育会誌, Vol.50, No.6, pp.74-77 (1968). http://ci.nii.ac.jp/naid/110003849391
直積の視覚的表現としてのアレイ図について,良書が見当たりませんのでアレイ図を書き,英訳も作りました.
ブログから:2×3をおはじきで表す
興味深く読みました.これまでのご経験を踏まえた,含蓄のある内容だと判断しました.
それはそれとして所感を手短に書いておきます*6.
- 「乗除は、おはじきを縦横に並べて2次元的にイメージできるし、その方が良いだろうということです」については,School Math Study Group (SMSG)の流行り廃りなどを含めた調査があったほうがいいと思います.
- 国内の書籍はというと,『板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉』と『新版 小学校算数 板書で見る全単元・全時間の授業のすべて 2年下』を読み比べたのを思い出します.かけ算の単元の最初が,前者は縦に並んだ40人をもとに分けるのに対し,後者(新版)は3行4列のアレイから始まっています.
- 上記の『新版…』と,記事に書かれた『学ぼう!算数 低学年用下 推薦学年2年』,そして本日の記事冒頭の出題から見えてくる共通点は,アレイはかけ算のモデル(文章題を解く際の手段)というよりは,かけ算の式で表す対象となるのではないでしょうか.アレイは交換法則や分配法則を表現するのには良いが,結合法則を表現するには不自由だ,というのも思い浮かびます.
- かけ算の導入より前に「まとめて数える活動」を行っている件についても,言及があると,安心して読めます.
- 中国の教科書を挙げていますが,ではそれを日本でも採用すれば,中国の後追いになるのではというツッコミには,どう答えるのがいいのでしょうか.「2001年」の教科書を見ていますが,その後「量の扱いではやはり不具合があって,教師たちの丁寧な対応によって乗り越えているところである」(http://www.nier.go.jp/seika_kaihatsu_2/risu-2-310_s-china.pdf#page=9)と指摘された件にはどのような対策があるでしょうか.
*1:これまで,6年生の4月下旬に受けており,出題の範囲は5年までの学習事項に限られていますが,それ以降の学習内容についても,出題があります.p.124にある,切手をばらばらにする数の文字式「3+7×(a-1)」は,なるほどと思いました.
*2:他人事のように書いていますが,自分としても担当科目(Cプログラミングとセキュリティ)の準備にあたり,考慮しないといけないことです.
*3:Amazonでは「(2014/1/7)」と表示されています.奥付には「2013(平成25)年12月26日 初版第1刷発行」と書かれています.
*4:魚拓をとっておきました:http://megalodon.jp/2014-0311-0532-05/d.hatena.ne.jp/takehikom/searchdiary?word=%C4%BE%C0%D1
*6:これはブログ主さんに答えてもらうというよりもむしろ自分用のメモです.