わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

かけ算と構造

OoM

はじめに

　この記事は，当ブログでこれまで記してきた「乗法構造（multiplicative structures，かけ算の構造）」に関する内容を集約することを目的としています．
　この集約は，次の問題意識と密接に関わっています．

  • 小学校の算数で学習が期待される「かけ算」とは何か?
  • 「かけ算」の学習について，小学校の教師や算数・数学教育の研究者はどのように考えてきたのか?
  • 乗法構造の知見を通じて，「かけ算の順序論争」に対して明快な視座を提供するのではないか?

おことわり：参考文献の表記について

　上記のとおり「集約」の目的としているため，記事には文献からの引用が多くなります．
　照合しやすくすること，記事の改訂・充実により増減があること，また出版年が重要な文献がいくつかあることから，「[著者名 出版年]」の書式で引用し*1，参考文献リストにも記載しています．ページ番号も必要な場合は，「[著者名 出版年, p.ページ]」や「[著者名 出版年, pp.開始ページ-終了ページ]」の書式を用います．
　当ブログの他の記事をはじめ，Web上の情報を参考文献に入れる際には，暫定的に[URL 番号]としています．
　本文中でのこれらの記号は，カッコ書きと同じ扱いとするほかに，「[著者名 出版年]では…」のように名詞としても使うことがあります．

1. 1983年と1988年のMultiplicative Structures

　「かけ算の『構造』って，何?」という疑問に対して，ある文献で明確に定義されている，というものは見当たりません．
　しかし，かけ算の学習に関する学術文献や書籍を開くと，「乗法構造」という言葉が，十分に確立された専門用語であるかのように，出現していることがあります．
　例えば[布川 2013]では，本文が「乗法構造は重要な学習内容であるにも関わらず」から始まっています．この文献では，乗法構造は，小学校でかけ算の指導をするなら知っておくべき概念である，というのことを前提としているように読めます．
　また別の，2013年の書籍にも，やや唐突な感での「乗法構造」の使用があります[齋藤2013, p.9]．「3人の友だちにみかんを4こずつあげます。みかんは全部でいくついりますか」という文章題で，3×4という式が正解か不正解かという検討にあたり，「算数・数学の問題解決を乗法構造という立場から特徴づけて捉えるベルニョの見解によれば」としています．その見解をもとに，正解とみなすべきかについては後述します．
　ベルニョはVergnaudと綴ります．「乗法構造」を英訳して "Multiplicative Structures" とすると，[Vergnaud 1983]および[Vergnaud 1988]の章題と一致します．
　ここで，[Vergnaud 1983]の概略を述べることにします．イントロのあと，Preliminary Analysisとして，著者の経験に基づく3つの乗法の構造，具体的には (a) isomorphism of measures（量の同型*2）, (b) product of measures（量の積）, (c) multiple proportion（多重比例）の考え方や問題例が詳しく述べられています．次に，Experimentsでは，日本でいう小学校6年生から中学校3年生の児童生徒に問題を解かせ，彼らなりの乗法の構造を浮かび上がらせようとしています．その後，Further Analysis and Experiments として，分数，（複）比例，ベクトル空間などに言及しています．残りのページはConclusionとReferencesです．
　(a)から(c)までのうち，最も分量をとって解説しているのは(a)のところです．中でさらに細分化されています．そこには，「a×b＝x」とは何なのかを示す，2種類の図が載っています(p.130)．


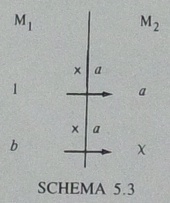
　前のページには，"two measure-spaces M1 and M2"と書かれています．measure-spaceは「量空間」と訳すのがよさそうです．
　「a×b＝x」の考え方について，直訳ではなく自分なりに解きほぐしていくことにします．
　まず，「1個15セントのケーキを4個買います．いくらになりますか」という問題を考えます．aを15セント，bを4個とします．xは60セントであって，60個ではありません．答えの数は15×4でも4×15でも求められるけれども，その答えが60「個」ではなく60「セント」となるのがどうしてなのかについて，2種類の解釈を示しています．前提として，SCHEMA 5.2, 同5.3とも，M1はケーキの個数の量空間，M2は金額の量空間です．
SCHEMA 5.2の考え方では，M1で1個から4個になるのを「×b」とします．同じ量空間における「b倍」を，M2へ適用することで，a＝15セントの「4倍」がx＝60セントになるわけです．
　このとき，「×b」のbは，もはや「4個」ではありません．あえて量という言葉を使うなら，無次元量です．
　SCHEMA 5.3は，横に見る関係といえます．1個だと15セント，という関係を「×a」で表します．そうすると，4個だと，「×15」とするので60セントです．
　ちょっと注意したいのは，この場面での「×15」は，数だけ見れば15倍ですが，実際には，M1という量空間からM2という量空間へ変換しています．あるいは，「×a」が，M1とM2という2つの異なる量空間の仲立ちをしている，と考えることもできます．
　このとき，「×a」のaは，これまた「15セント」ではなく，「15セント/個」とするほうが，より適切でしょう．言葉にすると，「1個（あたり）15セント」です．
　量空間は，数学的に定義しているわけではなく，同じ性質の集まりという程度と思われます．その一方で，数学的な取り扱いでの「量」だと，連続量（例えば[銀林1975, pp.32-43]）を対象とせざるを得ないところ，Vergnaudの議論では，ケーキの数や金額など，分離量も視野に入れています．
　ところで，比例を含む2つの数量の関係は，日本の算数であれば，2行（そして列数は任意）の表を作るのが一般的です．その際，行ごとに同じ種類の情報，すなわち同じ量空間の要素を書きます．そうすると，「縦に見る関係」と言いたいところです．実際，[田中2009, p.146]では，4マス関係表について「6年生になって表は縦に見ることもできるようになります」と書いており，その図式は，SCHEMA 5.3と同等となっています．
　この2種類の見方・考え方は，[Vergnaud 1983]を引用している国内の論文や書籍によく見られます[崎谷2000][岩崎2007, pp.157-160][柏木2011][渡会2012]．同じものを引用している海外文献，例えば[Schwartz 1988]や[Greer 1992]では，そのような見方がとられていないのと対照的です．
　また，SCHEMA 5.3を用いた解釈は，a×b＝xではなくb×a＝xを表しているのではないか，と考えることもできます．a×bとb×aの対比，という点では，[Vergnaud 1988]のほうがさらに踏み込んでいるので，以降はこちらの文献を見ていきます．
　[Vergnaud 1988]は，実験がないこともあって理論重視の構成となっています．そこでは，4×5でも5×4でもいいじゃないかと読むことのできる，以下の文章題が載っていました(p.144)．

1. コニーは4個のおもちゃの車を買いたい．1個は5ドルする．いくら払わないといけないか?
a) 5＋5＋5＋5＝20
b) 5×4＝20
c) 4×5＝20
d) 4＋4＋4＋4＋4＝20）

　なお，b)の式は原文では「4・5＝20」，c)は「5・4＝20」でした．和訳にあたりあえて，「×」を使い，「かけられる数×かける数」という，日本の算数の表記にしています．
　Connieだとかコニーだとかの前に「1. 」があるのは，かけ算に関する文章題と解き方(procedure)が何通りかあるためです．問題は5まで，解き方はn)まであります．2番目の問題の解き方は，「a)」と振り直すのではなく，「e)」となっています．そのようにして，異なる問題でも同じ式になる場合に，そこから共通点・相違点を探ろうという試みをしています．5)は長方形の面積問題で，「m) 4・5＝20」「n) 5・4＝20」という式もあるのですが，b)，c)と比較してこの場合には対称性があるよなあ，product of measuresであってsimple proportionとは別物だよなあ，と記されています．
　b)は，「5ドルが4つ」あるいは「5ドルの4倍」という関係であり，[Vergnaud 1983]におけるSCHEMA 5.2と対応します．c)について，「4×5＝20」における「4」は，おもちゃの車の個数です．「×5」は，「1個5ドル」という，車の数と価格とをかけ算によって結びつける操作を表します．
　ということで，5ドルのおもちゃの車が4個なら，総額を表す式は4×5でも5×4でもいいんだ，「3人の友だちにみかんを4こずつあげます」[齋藤2013, p.9]も，4×3でも3×4でもいいんだ，かけ算の順序問題は「どっちでもいい」で解決だ…
　というのがどうやら期待されていない記述が，[Vergnaud 1988, p.146]に見られます．原文と私訳を載せておきます．

The comparative facility of isomorphic over functional properties is even easier to show by considering all four procedures a, b, c, and d. Procedure b is a meaningful concatenation of procedure a. The cost of 4 cars = the cost of 1 car, plus the cost of 1 car, plus the cost of 1 car, plus the cost of 1 car. Expressed formally in terms of the isomorphic property for addition, this is f(1+1+1+1) = f(1)+f(1)+f(1)+f(1), and in terms of the isomorphic property for multiplication, f(4・1)=4・f(1). Procedure d is meaningless in terms of cars and costs. Twenty dollars cannot be 5 cars + 5 cars + 5 cars + 5 cars. Young students apparently are aware of this and never use procedure d. So there is a strong asymmetry between procedures b and c. They are not conceptually the same, although because of the commutativity of multiplication they may be mathematically equivalent.
私訳：同型性は，4つの手続きaからdまでをまとめて検討することで，より容易に示される．手続きbは，手続きaと意味をもってつながっている．4台の値段とは，1台の値段＋1台の値段＋1台の値段＋1台の値段である．加法における同型性を，式で表すと，f(1＋1＋1＋1)＝f(1)＋f(1)＋f(1)＋f(1)であり，乗法における同型性によって，f(4・1)＝4・f(1)となる．手続きdは，車の数と価格の観点から，無意味である．20ドルは，5台の車＋5台の車＋5台の車＋5台の車にはなり得ない．幼い生徒たちはどうやらそのことに気づいているらしく，決して手続きdを使わない．そのため，手続きbとcの間には強い非対称性がある．それらは，乗法の交換法則によって数学的には等しいかもしれないが，概念的には同一ではない．

　かけ算の式について，「幼い生徒たち」と，上の学年とで，正誤判定が変わってくることについては，[中野1957][守屋2011]でも示されています．同型性という言葉は，小学校学習指導要領に見られませんが，「横に見る（縦に見る）」などの見方は，第4学年D（数量関係）の「伴って変わる二つの数量」と関係してきます．
　そういったわけで，「3人の友だちにみかんを4こずつあげます」について3×4を正解とするのは，2年生の段階よりも，高学年でその意義を見出したいところです．2年生の授業では，3×4と書いたら，3＋3＋3＋3という式とともに，「12人になっちゃう」「みかんを3こずつ4人にあげることになっちゃう」といった解釈とともに，その式が場面に合わないことを確認するのは，「かけられる数」「かける数」そして数量関係の理解としてちょうど良いと言えます．これは，上記のa-dのうち，「c」よりも「a，b，dの組み合わせ」を重視しよう，ということでもあります．
　書いた式がどのように解釈され得るか，それを踏まえて我々はどのように答えを示せばよいかについて，余談として大学生向けに話したことがあります[URL1]．

参考文献

*1:細かいことをいくつか：著者名は姓のみで，複数の著者の場合は筆頭著者のみです．編著の場合は，該当箇所の著者が明確な（例えば章や項目の中で執筆者名が明示されている）場合にはその著者名を記し，そうでない場合は編著者名を記載します．

*2:分類名の和訳は，[岩崎2007, p.160]によります．