いきなりですが問題です.以下の図形において,色のついた部分の面積を求めましょう.
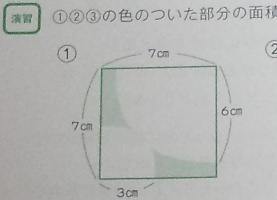
言葉にすると:1辺の長さが7cmの正方形の内部に,緑色をぬります.その頂点の1つを中心とし,半径3cmの円の内部に,白をぬります.対角の頂点を中心とし,半径6cmの円の内部に,白をぬります.そうして残った,緑色の部分の面積は,何㎠でしょうか.
さっそくですが元ネタと解答です.

- 作者: マルコ社
- 出版社/メーカー: サンクチュアリ出版
- 発売日: 2014/07/25
- メディア: 単行本
- この商品を含むブログ (2件) を見る
式はいいのですが,図が気になります.もし,2つの白でぬりつぶした円---正方形の内部だけを考えればいいので,以降はおうぎ形と呼ぶとして---に,重なりがあるのなら,2つのひき算で,2重取りをしていることになるからです.
しかし,2つのおうぎ形が,重なっても接してもいないことは,正方形の対角線に着目すれば容易に確かめられます.実際,対角線の長さは7√2cmです.√2≒1.4として概算すれば9.8cmですし,実際に測ってみても,9cmより長くなります.
それに対し,2つのおうぎ形の半径は,3cmと6cmですので,足して9cmです.中心間の距離が,9cm未満だったら,重なりが生じますが,上に書いたとおり9cmよりも大きいので,重ならないというわけです.
より正確な図を作ってみました.
長さは,変数svgの宣言より前に,まとめて記載しました.lenの中のr1とr2が,2つのおうぎ形の半径です.例えば,r1の値を4に変えて,「Run」を押せば,白が重なった図が表示されます.
本日取り上げた本は,親向けに丁寧に書かれているなと感じた一方で,アラも見られます.例えば前書きにあたるp.4には,「算数学習の本質は自分自身の頭できちんと考えていくことにあるのであって、公式の暗記にあるのではありません。」と書かれていますが,本文の各セクションは,「算数力ポイント」と題された,ルールあるいは公式をはじめに示し,あとはその適用問題,という流れになっているのです.速さについても,p.77に,道のり・速さ・時間の絵そして3つの公式が載っています.
かけ算の順序関連では,p.40のコラムに,「単位が異なっても計算できるのが、かけ算・わり算」として,「200円×3個=600円」の式が書かれています*2.その式における「個」の意味,あるいはなぜ積を求めると「個」が消失するのかについては,説明がありませんでした.
(最終更新:2014-11-10 朝)
