半分の面積の図形を描く

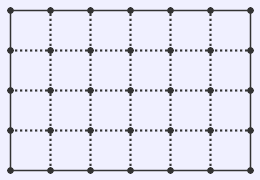
いきなりですが問題です．

以下の図から，4つの点を選んで結び，外周（長方形）のちょうど半分の面積となるような長方形をつくりなさい．

さっそくですが解答です．何通りもありますが，次の3つが基本形になります．

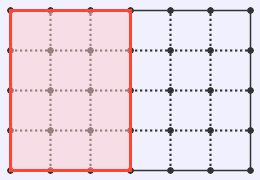
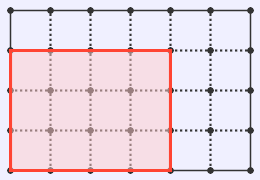
最初のは，縦に切って2分割したうちの1つ，2番目のは，横に切って2分割したうちの1つです．3番目のは，3×4＝12と求めてもかまいませんが，横の長さはもとの $\frac23$ ，縦の長さはもとの $\frac34$ なので，つくった長方形の面積＝もとの長方形の面積 $\times\frac23\times\frac34$ ＝もとの長方形の面積 $\times\frac12$ と書けば，小学校の分数のかけ算と関連づけることもできます．
他の図形にしましょう．さらにですが問題です．

以下の図から，4つの点を選んで結び，外周（長方形）のちょうど半分の面積となるようなひし形をつくりなさい．

以下の図から，4つの点を選んで結び，外周（長方形）のちょうど半分の面積となるような平行四辺形をつくりなさい．

以下の図から，4つの点を選んで結び，外周（長方形）のちょうど半分の面積となるような台形をつくりなさい．

以下の図から，4つの点を選んで結び，外周（長方形）のちょうど半分の面積となるような正方形をつくりなさい．

正方形ですね…いえいえ，これはつくれません．というのも，ちょうど半分の面積にするには，1辺の長さを $\sqrt{12}$ にしないといけないからです．この点の並び（正方格子）では，どの2点をとっても，その長さにできないことは，次のワンライナーで確認できます．

$ ruby -e 'puts (0..6).to_a.map{|x| (0..4).to_a.map{|y| x*x+y*y}}.flatten.sort.uniq.join(",")'
0,1,2,4,5,8,9,10,13,16,17,18,20,25,26,29,32,34,36,37,40,41,45,52

「0,1,2,…」の行では，原点と格子点(x,y)との距離の2乗として取り得る値を，小さい値から順に出力しています．3や12が出力に現れないのは，どの2点を選んでも，その距離を，最も近い2点間の距離の $\sqrt{3}$ 倍や $\sqrt{12}$ 倍にできないことを意味します．
そこで条件を緩めてみます．

以下の図の線上から，4つの点を選んで結び，外周（長方形）のちょうど半分の面積となるような正方形をつくりなさい．

(x,y)の一方の座標は整数でなくてもよいとすれば，作図が可能になります．その前に，少しばかり計算をしておきます．4点(0,a)，(b,0)，(4,b)，(a,4)を結んで，正方形をつくることとします．座標の条件より $a+b=4$ ，1辺の長さより $a^2+b^2=12$ であり，これらを解いて（a＜bとして）， $a=2-\sqrt2$ ， $b=2+\sqrt2$ を得ます．正方形は次のとおりです．

作図も，コンパスと定規があればできます．

(2,2)と(3,1)の距離を，コンパスで測り取って，その長さを，(2,0)から右に向ければ，(b,0)が求められます．残りの頂点も同様です．

本日の元ネタです．

山本良和のすべての子どもの心に響く算数授業づくりのコツ (算数授業研究特別号)

作者: 山本良和
出版社/メーカー: 東洋館出版社
発売日: 2015/02/20
メディア: 単行本
この商品を含むブログ (2件) を見る

(p.11)
これも東京で…ではなくて，関西に戻ってから書店で購入しました．「算数授業研究」の新刊は見当たらず，代わりに手に取った中に，いろいろ作図*1したり条件を緩めたり，あれこれ考えることのできる問題を見かけたのでした．
なお，本文では，この吹き出しの数行あとに「三角形，直角三角形，二等辺三角形，長方形，正方形，台形，ひし形…」と図形の候補が列挙され，次のページでは，「だから，会話の内容に当てはまる可能性があるのは，三角形，二等辺三角形，長方形（切り方によって），台形（切り方によって），平行四辺形，ひし形ということになる（ただし，階段のような形は除く）。」で段落を終えています．
もう一つ関連：