わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

四角形を描こう

math

　いきなりですが問題です．

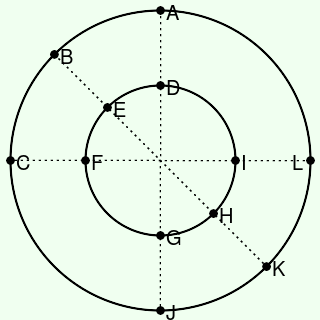
　図の点A～Lから，4つの点を選んで結び，図形を作ります．
f:id:takehikom:20190907120959p:plain
　以下の図形を作りましょう．
① 正方形
② ひし形
③ 長方形
④ 平行四辺形
⑤ 等脚台形
⑥ 台形
⑦ 凧形
⑧ ①～⑦のいずれでもない四角形

　2点，注意することがあります．図形の名称はいずれも，排他的とします*1．例えば「長方形」は，正方形でない長方形を意味します．そうしないと，正方形1つが①～⑦すべての解となってしまいます．
　もう一つの注意点は，各頂点の位置関係です．AJとCLは，大きい円の直径であり，円の中心で直交します．BKも直径ですが，円の中心をOとしたとき，∠AOCの二等分線の一部となります．なお，大きい円の直径は小さい円の直径のちょうど2倍として，描いていますが，これは必須の要件ではありません．
　といったところで解答例です．
① 正方形：ACJL
f:id:takehikom:20190907121004p:plain
② ひし形：DCGL
f:id:takehikom:20190907121010p:plain
③ 長方形：ABJK
f:id:takehikom:20190907121018p:plain
④ 平行四辺形：AEJH
f:id:takehikom:20190907121023p:plain
⑤ 等脚台形：DCJI
f:id:takehikom:20190907121029p:plain
⑥ 台形：ABEL
f:id:takehikom:20190907121038p:plain
⑦ 凧形：DFJI
f:id:takehikom:20190907121045p:plain
⑧ ①～⑦のいずれでもない四角形：ABGK
f:id:takehikom:20190907121050p:plain
　元ネタです．

算数授業研究 Vol.124　論究XV

算数授業研究 Vol.124　論究XV

　本記事では，4つの点を結びました*2が，授業は以下のようにしています(p.52)．

　これまでの四角形の学習は，4本の直線で囲まれた図形が見えているので，辺の長さや角の大きさの関係が見えやすかった。
　そこで，既習の図形を「対角線」で統合的に捉え直す題材を考えてみた。これは，大小2つの円の中にある12個の点のうち，4個を選んで直線を結ぶ。
　だがそれは4本の辺として引くのではなく，2本の直線だけを引かせる。つまり，子どもには四角形の全体像が見えない状態にある。その状態で四角形が何かを判断させるわけである。(以下略)

　この要領で，「2本の直線だけを引かせ」た状態の長方形は，次のように図示されます（原文では，ABJKの頂点名は書かれていません）．
f:id:takehikom:20190907121055p:plain
　子どもたちの反応が興味深かったので書き出します(p.53)．

　子どもは，①の正方形と②のひし形は，すぐに判断することができる。対角線が垂直に交わっていることと，対角線の端を結んだ形の四角形が見えやすいからである。
　一方，③の長方形と④の平行四辺形は分かりにくい。多くの子どもが③を平行四辺形と間違えた。どうしてか聞いてみると，「2組の辺が平行で，辺が斜めになっているように見えるから」と答えた。子どもは，対角線から端を結んだ形を想像していることが分かった。そこで，「③は対角線の交点からの長さを見てごらんよ。④と比べてみるといいですよ」と声をかけた。すると，③と④の対角線を比べて，③は平行四辺形ではないことを理解した。

　平行四辺形ではなく長方形，というのは，以前にサブブログで取り上げています．

　ところで，四角形ABJKが長方形であることを証明するには，どうすればいいでしょうか．元ネタでは，長方形の対角線を引いた図のすぐ下に，「［根拠］長さが同じで交点で2等分される。」と書かれています．「長方形の2本の対角線は，長さが同じで交点で2等分される」という性質（命題）の逆を，使用しているわけです．
　これ以外にも，直径に対する円周角が直角であることや，円の中心Oに関して∠AOB＝x，∠AOK＝y（このときx＋y＝180°）とおいて，三角形の内角の和と二等辺三角形の角度に注意しながら，∠BAKがx＋yの半分であることを導く（wikipedia:タレスの定理）といった方法が考えられます．


　画像生成はRubyスクリプトとし，ソースファイル（quadrilateral-drawer.rb）はGistで公開しました．
　「ruby quadrilateral-drawer.rb ABJK」のように実行すると，円と点線と頂点を描いた画像（base.png）と，その上にABJKを結んで長方形を描いた画像（ABJK.png)をカレントディレクトリに作成します．なお実行中にImageMagickのconvertコマンドを呼び出しています．
　引数なしで「ruby quadrilateral-drawer.rb」と実行すると（convertコマンドを使用せず，Rubyだけの処理となります），点A～Lから，4つの点を選んで結んでできる形状を一つ一つ判定し，最後に集計します．集計結果を並べ替えて，日本語を添えておきます．

             SQUARE:   16 figures（正方形）
            RHOMBUS:   16 figures（ひし形）
          RECTANGLE:   32 figures（長方形）
      PARALLELOGRAM:   32 figures（平行四辺形）
ISOSCELES_TRAPEZOID:  256 figures（等脚台形）
          TRAPEZOID:  128 figures（台形）
               KITE:  320 figures（凧形）
      QUADRILATERAL: 4128 figures（その他の四角形）
        INTERSECTED: 4576 figures（辺が交差のため四角形が作れない）
           COLINEAR: 2376 figures（3点が同一直線上のため四角形が作れない）

　INTERSECTEDになる例としてABKJ*3が，COLINEARになる例としてADFGがあります．
　いずれの値も，8の倍数です．これは，例えば正方形ACJLについて，4点をとる順序を変えることで，ACJLを含め8つの同一図形ができる（12点から4点をとる「数珠順列」となる）からです．また値の和は11880で，これは12点から4点を取って並べる総数となる，12×11×10×9と合致します．
　正味の図形の数はというと，正方形については16÷8＝2種類で，具体的にはACJLとDFGIです．ひし形も16÷8＝2で，図形はDCGLとAFJIの2種類ですが，これらは合同なので，実のところ1種類です．長方形は大小1つずつです．8で割っても516通りあるという，QUADRILATERALが何種類になるかを求めるのは，ちょっと大変そうです．

*1:https://takehikom.hateblo.jp/entry/20180404/1522783460（トピック2: 排反的な(exclusive)定義と包摂的な(inclusive)定義）をご覧ください．

*2:そのほか，元ネタの⑦も等脚台形だったのですが，本記事では，等脚台形でない台形を選びました．直線BKが，∠AOCの二等分線であることから，AL∥BKが言えます．

*3:長方形になるABJKと，点の順番が異なっています．順番が異なっていても，それぞれで四角形を作ることができるペアも見つかっており，例えばACEGとAECGが該当します．