どうして0でわっちゃいけないの?と図にするが,駄文にゅうすさんとこからリンクされました.感謝です.
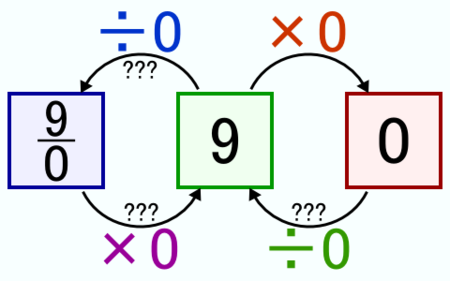
それで,図と,その直後の文章を見直したところ,4÷5,9÷0,8÷0の値はそれぞれ,分数で書くほうが自然なことに気づきました.
図を修正します.
(e) 一つめの数が8,二つめの数が0
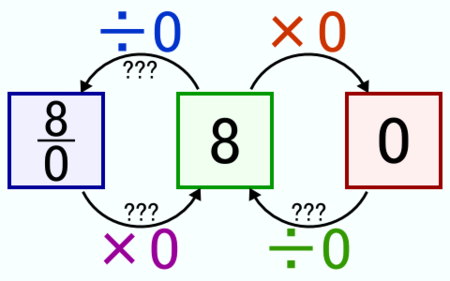
「(b) 一つめの数が6,二つめの数が6」と「(c) 一つめの数が0,二つめの数が8」は変更ありません.それと,冒頭で書くべきだったのですが,本日のエントリは小学校3年生に話せる内容を大幅に超えています.
図の左半分も,見直しておきます.9÷0×0=9,8÷0×0=8を満たすよう,9÷0の答えの「0」と,8÷0の答えの「0」とを,区別するという方法は,どうでしょうか.例えば,分数と同様に,一つの数を,分子と分母にあたる2つの整数の組であらわし,分母が0になってもよいという考え方です.分数と同様の演算(加減乗除,通分・約分)を認めれば,9÷0×0=(9/0)×0=9と計算できます.ですがこの場合には,9=8が証明できてしまいます.
図にする
上の内容をリリースする前に,メモ書きしていた,証明の概略は次のとおりです.0/9×9/0=1および0/8×8/0=1より,0/9×9/0=0/8×8/0.両辺に左から72/1をかけると,左辺=72/1×0/9×9/0=(8×0/1)×9/0=0/1×9/0,右辺=72/1×0/8×8/0=(9×0/1)×8/0=0/1×8/0.さらに両辺に左から1/0をかけると,9/0=8/0.両辺に0をかけると,9=8.証明終.なのですが,使用した性質を書き出すのも,大変です.
数日考えていて,もっと楽なのが見つかりました.9÷0×0=9/0×0=9が成立する,すなわち「9/0」を分数のように扱えると仮定したとき,9/0×0×0を計算すればいいのです.9/0×0×0=(9/0×0)×0=9×0=0,9/0×0×0=9/0×(0×0)=9/0×0=9が得られるので,0=9です.ここで9は,任意の数に取り替えることができます.9=8でも何でもご自由に,となります.
この導出をもとに,次のことが言えます.すなわち,実数全体からなる集合Rに対して,その零元0が逆数0^-1を持つようなR'を構成します.その際,0^-1が含まれる演算は適宜定め,含まれない場合には実数体Rにおける演算と同じとします.以上の仮定のもとで,R'は乗法の結合法則を満たしません.
その際,0^-1を∞と書いてR'=R∪{∞}としても,0^-1をRの中から選んで(例えば0^-1=0),R'=Rとしても,そのことは論証に影響しません.不可欠なのは,R'が,加法と乗法について閉じている(そのように,Rを拡張しつつ適宜定める)ことです.
そう考えていくと,自分の関心が「9÷0は何か?」「0÷0は,どんな値になるべきか?」ではないことに気づきます.「なんとか÷0」が一つの値になるよう,わり算を定めると,それまで成り立っていた演算の性質が成り立たなくなるか,または数は「0」だけになる(8も9も,0と同一視しなければならない)という次第です.
んで駄文にゅうすさんとこからリンクされている,四一郎さんの「0で割る話」 - Togetterも読みました.本編の,
が,最もわかりやすい3年生向けの説明になっていると思います.
後ろのコメントが長くて驚きですが,何とか読み通しました.かけ算の順序論争もほんのり入っています.足算と引算と割算のそれぞれで,二つまたはそれ以上に分類できるのを認めていながら,掛算に対してもそういった分類ができる*1ことを言及しないってのには,ふたたび驚きでした.
言うまでもなく個人的には,このゼロ除算の件と,いわゆるかけ算の順序論争を,並べるのには無理があると思っています.ゼロ除算については,学習指導案(というより,ゼロ除算を学習したとしてそれが将来,何に活用できるかの検討)も,1個の学級・学校を超えた外在的評価のためのテスト問題も,見たことがないし探しても無駄だからです.
(最終更新:2012-12-14 早朝.駄文にゅうすさんとこのURLを変更し,(d) (e)の図を正しく配置しました.)
*1:頭の中で「できる」にとどまらず,文献もいくつかあります.用語:倍と積 - 「×」から学んだこと@wiki - アットウィキで整備しています.