「乗法構造」の俯瞰図と呼べるものがあります.
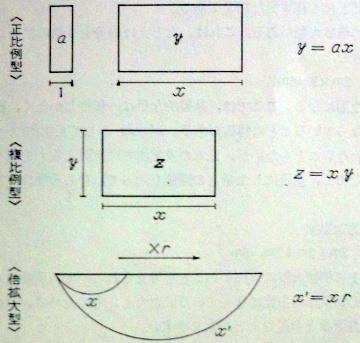
(『数学の世界―それは現代人に何を意味するか (中公新書 317)』p.72 *)
1973年の書籍に収録されており,作成者は森毅です.小学校で学習するかけ算は,〈正比例型〉〈複比例型〉〈倍拡大型〉に大別でき,それぞれの因数(被乗数・乗数)の役割が明らかにされています.
世界的には,乗法構造といえば1983年および1988年にVergnaudが書いた"Multiplicative Structures"の内容を指します.上記の〈倍拡大型〉と〈正比例型〉はそれぞれ,次のように図式化されています(isbn:012444220X p.130 *).

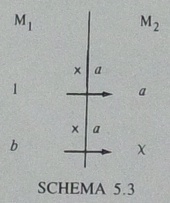
これまで読んできた書籍などを見直し,文献リストを作成しました.
- 1970年代の乗法構造
- 1983年と1988年の乗法構造
- Vergnaud, G. (1983). Multiplicative Structures. In Lesh, R. and Landau, M. (Eds.), Acquisition of mathematics concepts and processes, Academic Press, pp.127-174. isbn:012444220X ***
- Vergnaud, G. (1988). Multiplicative Structures. In Hiebert, J. and Behr, M. (Eds.), Number Concepts and Operations in the Middle Grades, Vol.2, pp.141-161. isbn:0873532651 **
- 英文に見る乗法構造
- Anghileri, J. and Johnson, D.C. (1988). Arithmetic Operations on Whole Numbers: Multiplication and Division. In Post, T.R. (Ed.), Teaching Mathematics in Grades K-8, Longman Higher Education, Allyn and Bacon, pp.146-189. asin:0205110762 ***
- Greer, B. (1992). Multiplication and Division as Models of Situations. In Grouws D.A. (Ed.), Handbook of Research on Mathematics Teaching and Learning, National Council of Teachers of Mathematics, pp.276-295. isbn:1593115989 **
- Schwartz, J. L. (1988). Intensive quality and referent transforming arithmetic operations. In Hiebert, J. and Behr, M. (Eds.), Number Concepts and Operations in the Middle Grades, Vol.2, pp.41-52. isbn:0873532651 *
- Park, J.-H. and Nunes, T. (2001). The development of the concept of multiplication, Cognitive Development, Vol.16, Issue 3, pp.763-773. **
- Vergnaudを引用した日本語文献
- 『算数・数学科重要用語300の基礎知識』*
- 渡会陽平, 小学校算数科における乗除法の意味に関する学習過程の分析―G. Vergnaudの概念野理論を枠組みとして―, 数学教育学論究 (日本数学教育学会誌臨時増刊), 日本数学教育学会, Vol.97, pp.3-16 (2012). http://ci.nii.ac.jp/naid/110009518193/ *
- 『授業に役立つ算数教科書の数学的背景』*
- 「乗法構造」を含む日本語文献
- 布川和彦: 比の学習における小学生による説明と式の利用, 上越数学教育研究, No.28, pp.1-12 (2013). http://ci.nii.ac.jp/naid/120005265721 *
算数教育のかけ算では,〈正比例型〉〈倍拡大型〉に当たるものが広く研究されており,〈複比例型〉は,あまり脚光を浴びていませんでした.当ブログではこれまで,以下の記事で検討を試みてきましたので,どうぞご確認ください.