いきなりですが問題です.
面積が2,5,および10の正方形を活用して,√2×√5=√10を示してください.ただし三平方の定理を使用してはいけません.
面積が2および5の正方形を活用して,√2+√5≠√7を示してください.ただし三平方の定理を使用してはいけません.
本日の記事では,正の実数aに対する正の平方根を√aと表記します.面積がaの正方形の一辺の長さは√aとなることをはじめ,平方根の性質は既知とします.またaの2乗はa^2と書きます.
今回の問題の元ネタです.

- 作者: 永田潤一郎
- 出版社/メーカー: 明治図書出版
- 発売日: 2017/10/13
- メディア: 単行本
- この商品を含むブログを見る
- 永田潤一郎(編著): 平成29年版 中学校新学習指導要領の展開 数学編, 明治図書出版 (2017). isbn:9784183343185
√2+√5≠√7を示すための図が,p.107にあります.
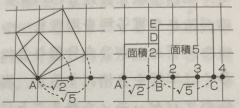
正方格子上の点をうまくとることで,1つの点(上図ではA)を頂点に持つ,面積2と5の正方形が描けます.これを回転し平行移動すると,1つの直線(AC)上に,2つの正方形の一辺ずつが横並びとなります.そして,1<√2および2<√5なのが分かります*1.この2つの不等式の左辺・右辺ごとに,たし算をすると,3<√2+√5が得られます.
正方格子上の点を選んで面積7の正方形をつくることは,できませんが,面積7の正方形と,面積9の正方形とを比較することで,面積だと7<9,一辺の長さに関しては√7<3が言えます.
これらより√7<3<√2+√5となり,√2+√5≠√7が示せました.
次に√2×√5=√10を考えます.上記の本のp.106です.

3つの図が,縦並びになっています.上にあるのは,2×3=6を表す二重数直線であり,本文には「2×3の計算を思い出し,それと同様に考えることができないかを考察できるようにすることが考えられる」とあります.
2番目の図は,三角形の相似を用いた、2×3の説明です.「1」と「2」,「3」と「x」を結ぶ2つの直線が平行であることから,それらの辺と「0」の頂点とを結ぶ2つの三角形が相似となり,「相似な図形は未習であるが,直感的に1:3=2:xと表すことができ,x=2×3であることは理解できるだろう」とのことです.
3番目の図は,2番目の図について「2」を「√2」に,「3」を「√5」に置き換えたものです.「右の図のように面積10の正方形をかきその1辺と√2×√5が一致することを図のように示すことができる」となっていまして,「面積10の正方形をかきその1辺と√2×√5が一致する」については,コンパスで同じ幅になることを確かめるものと思われます.なお,「面積10の正方形」となることは,正方形・正三角形をつくるにて検証済みです.
ともあれ,この3番目の図が分かりにくかったので,2次元平面の性質に着目して自分なりに検討してみました.以下のように点をとります.
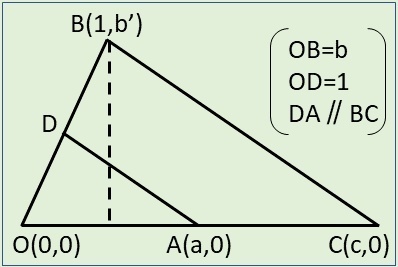
O(0,0)は原点とし,A(a,0),C(c,0)とともにY座標の値が0なので同一直線上に並びます.B(1,b')について,X座標は1で,原点からの距離をbとします.三平方の定理により,1+b'^2=b^2という関係が成り立ちますが,以下では使用しません.a,b,cのいずれも正とします.示したいのはab=cです.
半直線OB上に,原点からの距離が1となるような点を見つけてDとします.するとOB:OD=b:1となり,OD=(1/b)OBと変形することで,Dの座標を(1/b,b'/b)と表せます.
直線DAの傾きは,(AのY座標−DのY座標)/(AのX座標−DのX座標)=(0−b'/b)/(a−1/b)=−b'/(ab−1)であり,これをkとおきます.
DとA,BとCを結ぶ2本の直線が平行であること,すなわちDA‖BC*2は,直線DAの傾きと直前BCの傾きが等しいことを意味します.直線BCの方程式は,点Bを通って傾きがkであることから,y−b'=k(x−1)と表せます.この式において,y=0のときのxの値がcすなわちCのx座標です.0−b'=k(c−1)をcについて解くと,c=1−b'/k=1−b'(ab−1)/(−b')=1+ab−1=abとなり,めでたくab=cが示せました.
√2×√5=√10に話を戻しますと,a=√2となる点Aは,正方格子上で面積2の正方形を描いてから45度回転させることで,得られます.点Bについてはb'=2とすればOB=√5になります(OBを一辺とする正方形の面積が5となります).c=√2×√5なのですが,あいにく今回の図と論証では,これが√10に等しいことを示すことができず,結局,コンパスで同じ幅になることを確かめる必要があります.