さいしゅう

昨年末あたりから購入したり書き写したりしていたものを，いくつか公開します．
本日は複数の箇所で，「《ＢＡ型》」というラベリングを使用しています．これは，文章題で，Ａ，Ｂの順に数が現れ，Ｂ×Ａ（＝Ｐ）の形で式に表すことが期待される問題のことです．

1. 九九をおぼえよう!

九 九 をおぼえよう! STD-725A K61A [DVD]

30分ほどのDVDです．「博士」と「男の子」と「女の子」が登場します．内容の大部分は，各段の九九ですが，最後の文章題では，《ＢＡ型》に対してＡ×Ｂ＝Ｐ，すなわち数を出現する順に使って，かけ算にするのを，正解としています．

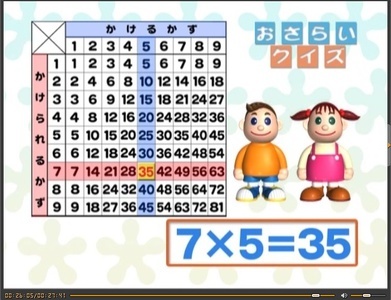
博士「では，ここで，おさらいクイズを出すぞ」
男の子「ようし，がんばるぞ」
女の子「わたしも」

博士「おともだちが7人，おうちに遊びに来ました」

博士「そして，おやつの時間，みんなにキャンディを5個ずつあげました」
博士「では，キャンディは，全部で何個，おともだちにあげたのかな?」

博士「九九早見表で，答えをさしてごらん」
男の子「えっと，おともだち，7人に，キャンディを，5個ずつあげるんだから，かけざんの式にすると…」
女の子「7かける，5で，いいのかしら?」

博士「そうじゃ」（正解のベル）
博士「では，九九早見表で，調べてごらん」
女の子「かけられる数っていうのが，7になって」
男の子「うん，かける数っていうのが，5で」
男の子「ぶつかった数は，35」

男の子「おともだちにあげたキャンディは，全部で35個だ」（正解のベル）

博士「正解じゃ，よくできました」

著作・販売は[http://www.keep.co.jp/:title=キープ株式会社]です．

2. 新・算数指導の疑問これですっきりIt's OK!

新・算数指導の疑問これですっきり―It’s OK!

学校の先生向けのQ&A集です．
「第6学年の問題」の，連続する問いの答えに，次のような文字式が書かれていました．

• 「5×x」は，「x円が5個」というように，「数量についてのことがら」を表す式
• 「5×x＝y」は，「yは5のx倍」というように，「数量の関係」を表す式

(p.107)

ちなみに，x×6＝240のxは，未知数（分からないが決まっている数）として用いられており，1本x円の鉛筆5本の代金をx×5（円）と表す場面でのxは変数（いろいろな値をとりうる文字）として扱われる。
(p.107)

小学校で書く文字式については，黒木玄氏によるこちらで整理されています．当ブログではこちらで「8×x」という項目を設けて検討を試みました．「x円が5個」は「x×5」と書くのが自然だと思う一方で，「5×x」が「x円が5個」と解釈し得る(may be interpreted)ことについては，「まあそうですね」という認識です．
本に戻ります．「第2学年の問題」には，いわゆるかけ算の順序の話はありません．九九を何の段から教えるのがよいかという問いへの回答で，「乗法九九の指導の順序については…」として，「順序」の文字が見られます．
「第3学年の問題」の問1は「等分除と包含除の違い」です．等分除先行となっています．
(p.46)
問2は，48÷6の計算で，九九から答えを出すには，「六八48」，すなわち除数を先に唱えることとしています．

3. 算数力アップ!新評価規準ワーク&授業づくりマニュアル2年

算数力アップ!新評価規準ワーク&授業づくりマニュアル 2年

(3) 絵を 見て，しきを かきましょう。また，その答えは，九九ひょうの どこに なりますか。色を ぬりましょう。

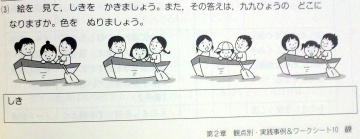(p.69)
式は「3×4＝12」です．
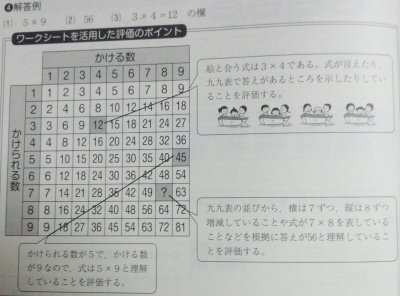(p.68)
この2ページの「本時のねらい」は，「かけ算九九表や問題場面を読み取ったり，乗法の式の意味や答えの求め方を理解したりすることをねらっている。」(p.68)となっています．
a×bかb×aか，いやどっちでもいいのだ，という出題は，見当たりませんでした．ただし，単元計画の中には，「基準量があとに示された適用題を解く」(p.51; 関連)が，1時間の授業として組み込まれています．

4. イメージづくりが勝負の算数指導のポイント

イメージづくりが勝負の算数指導のポイント

(略)
最近では、文章題どころか計算のつまずいている子がふえています。
いったい、こういうつまずきがなぜ起きるのでしょうか。
その大きな理由は、“意味”を正しく教わっていないからだと思います。
例えば、3×4の意味は、「3を4回たすことだ。」と考えていませんか。（もちろもこういう意味もありますが）そうすると、
3×1＝6　（なぜなら、3＋3＝6　1回たした）
3×0＝3　（なぜなら、3＋0＝3　0回たした）
とまちがえる子がいても不思議ではありません。
さらに、小数になると、3×1.2など、まったく説明がつきません。（1.2回たすなんてあり得ないからです）。「の×、が÷」と覚えるしかないのです。
これでは、算数ぎらいがふえてもおかしくありません。
私は、つぎのような授業をしました。この方法だと、家庭でも教えられるのではないでしょうか。
「たすの?」「かけるの?」からはぬけ出すためには、
①かけ算のイメージを豊かにする。
②意味をしっかりつかませる。
③かけ算の構造（かけ算図）をはっきりつかませる。
ことが大切です。
(pp.34-35)

上記に明らかな誤字も入っていますが，可能な限り原文のままとしました．
当ブログでこれまで書いてきた，数教協スタイルです．数教協スタイルはこちらの出だしで整理を図っています．
式・図は次のとおり．
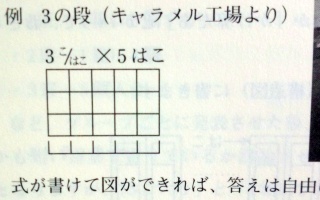(p.38)
かけ算の意味づけを除けば，優しく書かれており，教師向けでありながらも家庭で読むにも良い内容です．
「小学校の算数で，これだけわかればいい」の中で，かけ算が簡明にまとめられていました．

③かけ算
a. 「みかんを1人に 5こずつ くばります。7人では『ぜんぶで なんこ いりますか』」といった
（1あたりの量）×（いくつ分）＝（全体量）
が典型です。
b. 「ある店では 仕入量の 130%の値段で 売ります。仕入値が 700円の品物の 売値は 何円ですか」というのが“倍”の問題で、
（基になる量）×（倍）＝（くらべる量）
となります。
c. （長さ）×（長さ）＝（面積）
（面積）×（長さ）＝（体積）
（労働人数）×（労働日数）＝（労働人日）
のように、新しい乗法単位がつくられるものがあり、これは4年生以上に出てきます。
(pp.147-148)

筆頭編著者の笠井一郎は神奈川数学教育研究協議会委員長とのこと．他の編著者・執筆者も，「神奈川数学教育研究協議会」の所属が入っています．

5. 小学校学習指導要領の展開 算数科編

• 和田義信(編): 小学校学習指導要領の展開 算数科編, 明治図書 (1960).

大学図書館で，主要なところを書写しました．

記号（X）を正しく用いるために加法との関係をもとにして，その意味を理解させるとよい。
　　4＋4＋4＝4×3
のような形式を目からも印象づけておくと，記号の意味がはっきりつかめるようになろう。
乗法に関して交換の法則が成りたつことは第3学年の内容であるが，その際，子どもは，何を何倍するかという乗数と被乗数とのもつ意味に混乱を起こし易い。
そういう混乱を防ぐ意味でも，先ず乗数と被乗数との関係を明確にしておくことが必要である。計算上の交換の法則と数量関係における乗数被乗数の関係は，注意深く指導すればはっきり区別していくことができるものである。このことは，分数や小数の乗法について学習するようになって，大きな障害を生むか生まないかの重要な要素ともなるので注意を要する。
(p.143)

たとえば，「ひとり分が3mのひもを4人分ほしい。ひもを何m買ったらよいか」というとき，3mの4ばいの長さを買えばよいことがわかる。
3mの4倍をもとめることを，3×4と書いて，「3かける4」と読み，この計算を「かけざん」と呼ぶ。
結果を求めるには，4倍とは等しいものの4つぶんのことであるから
　　3×4＝3＋3＋3＋3
ということで，たし算によって結果を求めることができる。
(pp.143-144)

④乗法の交換の法則，結合の法則について
乗法の交換の法則の指導については，被乗数は，累加されていく数（グループ）であり，乗数は累加する回数（個数）であることを理解している子どもたちに対しては，単に，「被乗数と乗数をとりかえてかけても，積は変わらない」という形式的な説明をするだけでは，納得しないかも知れない。
この点具体的に明確に指導することが大切である。特に交換の法則は，積は変わりがないが，その積が変わりがないということのために，a×bとb×aの式が同じであると混同するものがでてくる心配がある。それで，式としては違うことを明らかにすることが大切である。
(p.171)

3つに分けて引用したうち，1番目と3番目で共通しているのは，「□×△と△×□，答えは同じだけど，意味は違う」です．1番目と2番目は，累加に基づく，4×3と3×4の違いの例示です．個人的な記憶ですが，中1の英語の教科書で，「he」という代名詞と，「hi」という間投詞の初出が同じページでした．似て非なるものであり，区別して覚えようという意図だったと思います．
交換の法則を巡る「混乱」「混同」の，2011年バージョンとして，『かけ算には順序があるのか (岩波科学ライブラリー)』が思い浮かびます．p.89に，「かけ算の交換法則を教わりながら，式は「1あたり量×いくつ分」の順序で書け，と言われて戸惑ういまの子どもたちが思い浮かびます」がカッコ書きで記されています．
本に戻ります．除法は等分除先行でした．例として「12本÷3＝4本（等分除）」「12本÷3本＝4（包含除）」(p.172)という式が見られます．また式に単位を付けることについても，「低学年は別として，中学年以上では，式については，名数を用いない方がよい．」(p.174)と言及されていました．

6. 「小学算術」の研究

• 高木佐加枝: 「小学算術」の研究, 東洋館出版社 (1980). ◆

これは新たに読んだ本ではありません．一つ上の本を図書館で見たときに，ついでに読み直したのでした．
蛸の足の数の初出と思える出題が，目に留まりました．

（例3）
（図省略）
タコガ，八ヒキデ ヲドッテ ヰマス。アシハ ミンナデ 何本アルデセウ。マタ二ヒキ 来マシタ。アシハ，何本ニ ナッタデセウ。〔小算二上 p.78(4)〕
(p.146)

8×8＝64なので，a×bもb×aもありませんね．なお，緑表紙教科書に《ＢＡ型》の出題が入っているらしいことは，はてブしています．
本に戻ります．次の例4は順列を扱ったもので，3年向けの問題です．それと，児童に問題を作らせる，いわゆる「作問」は緑表紙からとのことです(p.204)．

7. 算数の復習小学2年―もっともたいせつな標準問題をひとつひとつ。

算数の復習小学2年―もっともたいせつな標準問題をひとつひとつ。

新学習指導要領対応をうたった問題集なのですが，目次を書き出しておきます．

14　ばいと かけ算……………………………28
15　かけ算(1)（2・5のだん）………………30
16　かけ算(2)（3・4のだん）………………32
17　かけ算(3)（6・7のだん）………………34
18　かけ算(4)（8・9のだん）………………36
19　かけ算(5)（1のだん・九九のひょう）…38
20　かけ算の もんだい………………………40
（もくじ）

「倍」で意味づけを図っています．

「1つ分の数」をはっきりつかみます。
1つ分の数×いくつ分（なんばい）＝ぜんぶの数となります。
（考え方と答え p.9)

かけ算の立式や計算について，他の問題集と大きな違いは見られません．
と思いきや，《ＢＡ型》が，3要素2段階の問題（関連）の中に現れます．

[5] つぎの もんだいに 答えましょう。
① 7人の 子どもに あめを 5こずつ くばったら，3こ あまりました。あめは いくつ ありましたか。
(p.31)

答えと解説は以下のとおり．

[5]① （しき）5×7＝35　35＋3＝38　（答え）38こ
（考え方と答え p.10)

[5]①「1人に 5こずつ 7人にくばる」ので，くばったあめの数は5×7＝35(こ)で，まだ3こあまっているから，35＋3＝38(こ)となります。
（考え方と答え p.10)

8. 陰山ドリル算数文章題小学2年生

陰山ドリル算数文章題小学2年生

[3] 水そうが 4つ あります。どの水そうにも、水を 8Lずつ 入れます。
水は 全部で 何L いりますか。
(p.65)

《ＢＡ型》です．8の段に出てきます．別冊子になっている答えを確認…「しき　8×4＝32」「答え　32L」でした．
各問題は，図やなぞり書きを取り入れ，かけ算の式の表し方を誘導しています．そして別冊子の答えの中に，「かけ算の順序」の注意書きが入っていました．

九九の問題に入ります。
九九の問題では，「かけられる数×かける数＝答え」に注意して解きましょう。文章題では「かけられる数」「かける数」が逆になると，答えが正解でも式で減点されてしまいます。かけられる数（1あたり量）をしっかり押さえて考えましょう。
（答えp.6）

9. まとめ

本日行ったのは，昆虫採集，植物採集の標本づくりのようなものでした．
《ＢＡ型》は，自分の関心の一つです．これに注意して問題集や指導例を見ていくと，それぞれの特色が見出しやすいのです．
ここで，「かけ算の順序」論争の実用面からの批判を，見直すことにします．そこではよく，会計や海外の事例を中心として，「あれもある」「これもある」を経て，「いろいろあるね」「どっちでもいいじゃないか」に持っていっているように感じます．
しかし算数教育，とりわけ問題解決学習（問題解決型の授業）では，「あれもある」「これもある」のあとに「ではどうしよう」と，クラスの中で検討することになります．あれもこれも正解，という場面でもまた，「ではどうしよう」すなわちそこで学習したことを，今後どのように活用していけばいいかを確認するという，「練り上げ」と呼ばれる活動が，重視されています．
単純に言うと，論争は「いろいろあるね」と「ではこうしよう」との間のせめぎあいなのです．
そのもとで私は，「ではこうしよう」とする，今の算数教育を支持します．理由の一つは，そこから過去-現在-未来のつながりが見えることです．もう一つは，自分自身が日常においても工学研究においても，複数の選択肢の中から「答え」を見つけたり選んだりしており，子どもたちにもそのように主体的に判断・行動してほしいと願っているからです．
ここまで書いたことに，補足が3つあります．批判者も「いろいろあるね」と「ではこうしよう」を使い分けていますし，学校の先生方も，また私自身も，「いろいろあるね」と「ではこうしよう」の要所要所での使用を見ることができます．複数の選択肢の中に，正解は一つかもしれないし，複数あるかもしれません．そして選んだ「答え」は，その時点では必ずしも，正解であると保証されていません．
などと考えたりするものの，かけ算の出題・指導の標本づくりの結果は，「いろいろあるね」でも，「ではこうしよう」でもなく，「まだまだ学ぶべきことがあるなあ」なのでした．

（最終更新：2013-03-02 晩．番号を振りました）