「http://d.hatena.ne.jp/takehikom/searchdiary?word=*[5×3]」でお越しの方へ：2013年3月より，「かけ算の順序」関連の記事には [OoM] というカテゴリーをつけています．総集編1・総集編2も，どうぞご覧ください．
本日は，トランプ配りの等分除への適用について検討します．かけ算の文章題などでトランプ配りを適用しようとする話は，トランプ配りと，うまくやっていくや配る（3. 猫にキャンディ，3×2とできるか?）で書いてきました．国内外の本や論文から知り得る限り，かけ算に適用しようとする先生も授業例も，子どもたちの認識というのも，見当たりません．
「トランプ配りの等分除への適用」を問題意識として，昨年末あたりから書籍を見ていくと，妙な共通性に気づきました．分ける対象が，一列に並んでいるのです．
手元の本から，例を挙げます．
■Anghileri＆Johnson (1988)
(FIGURE 6-1, p.147)
[f:id:takehikom:20130227051639j:image](p.156)
[f:id:takehikom:20130227051640j:image](p.160)
■Greer (1992)
（p.281; dealing out）
■教科調査官が語るこれからの授業 小学校―言語活動を生かし「思考力・判断力・表現力」を育む授業とは
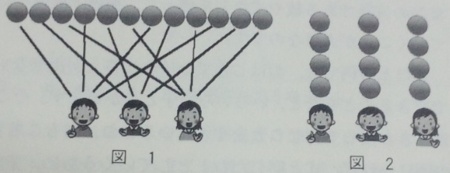（p.71; 2012年のトランプ配り）
■アイディアシートでうまくいく! 算数科問題解決授業スタンダード
（pp.57-58; 関連：2. どっちの式でもいいのかな - 北数教）
ここまでいずれも，配られる対象が一直線になっています．
それらを目にして，「数を大きく見せる手法」（後述）を連想しました．最後の板書例は，「クッキーが□こあります」として，その総数が最初に明示されていませんが，それでも，配る人数が決まっていることと，1個ずつ取り出せることを前提とすれば，配っていくことができるわけです．
等分除を，アレイ図で表現する事例も，あります．
4.1.2 除法の素地
先に述べた乗法の素地となるような経験は，見方を変えれば，いずれも除法の素地にもなっている。例えば，数えることに関しては，「8個のみかんは，2個ずつまとめて数えると4回になる。」などという見方ができるようにする（図1）。これはまた，減法で表すと，8−2−2−2−2で数え終えたことになる。
また，分配を，計算とは別に，実際にそうさせることもある。例えば，「8個のみかんを4人に分けるにはどうしたらよいだろう。」などという場面を考え，各人に1個ずつ配り，まだ余りがあったらまた1個ずつ配るという活動をさせる。
(pp.144-145)
（図1）
■算数科「問題解決の授業」に生きる「問題」集
（p.85; 3年のわり算かけ算）
アもイも正解です．問題解決学習では，「アが正しい」，「イが正しい」，「どちらも正しい」という反応を出させてから，アは等分除，イは包含除でどちらも正しく，「わり算は，同じ絵でも式が違う場合がある」とまとめることになります．
木村教雄『小学算術教材ノ基礎的研究』には，「包含除の本質は累減にあると見ることが出来る．」と書かれていました．
これと同様に，トランプ配りとは何なのかを，表現することができそうです．すなわちトランプ配りの本質は，等分除に対する累減の操作にあると言えます．
減らすためには，「減らす分（数量）」が定まっていないといけません．
トランプ配りは，減らす分＝配る分が「1個」と，明らかです*1．
逆に言うと，昨日の記事で例示した，ショウユや糸を等しい量（かさ・長さ）に分けようとすると，累減のための「減らす分（数量）」が自明ではありません．
字数を増やしていいのなら…トランプ配りの本質は，分離量を対象とした，等分除を実現するための累減の操作にある，といったところでしょうか．
「数を大きく見せる手法」について補足します．
以前に30分×10人＝300分を書きました．これは，かけ算によって，大きく見せられるというものです．
小学校学習指導要領解説 算数編 p.65にも，見ておくべきものがあります．1年向けですが，8本の鉛筆を2本ずつや4本ずつに分ける話です．これを読む際に，注意しないといけないのが2つあって，一つは，1年生にとって「8つ」という数が必ずしも，具体物・半具体物を見ても瞬時に認識できるとは限らないこと，もう一つは，この分け方は包含除によるものである点です．
同じページに，「具体物を等分することについては，全体を同じ数ずつ幾つかに分けたり，全体を幾つかに同じ数ずつ分けたりする活動を扱う」とあります．表記上は，包含除と等分除を同等に扱っていて，その2種類の分け方が，除法の素地となるわけです．しかしそのあとの例示や，ページ下段の8つの○の分け方，そして添えられている式を見ると，ここもまた，包含除先行・優位であるように見えます．
もし，等分除先行・優位（もしくは，包含除と等分除の同等性）を押し進めていくだとか，トランプ配りの乗法への適用を，算数教育において確立しようとするなら，この段階から，素地となるような工夫が必要なように感じます．
（リリース：2013-02-27 早朝）
（最終更新：2013-02-27 朝）
*1:配る際に，配る分が常に同じである必要は，ありません．360円（百円玉3枚と十円玉6枚）は，3人に120円ずつ渡すことができます．「1回に配る分」が同じであれば十分です．
