□×△と△×□の違い：事例

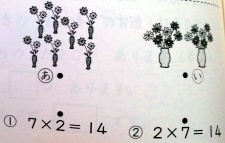
いくつか書籍を入手しました．過去に書いたものと合わせて，「□×△」と「△×□」が違う，あるいは，かけ算で2つの数が反対になると意味が異なるとしているものを，一覧にしてみます．

算数に強くなる水道方式入門（1961年）

算数に強くなる水道方式入門 (1961年)

(p.183)
関連：水道方式入門(1961)のトランプ配り

Arithmetic Operations on Whole Numbers: Multiplication and Division（1988年）

• Anghileri, J. and Johnson, D.C. (1988). Arithmetic Operations on Whole Numbers: Multiplication and Division. In Post, T.R. (Ed.), Teaching Mathematics in Grades K-8, Longman Higher Education, Allyn and Bacon, pp.146-189. asin:0205110762

For children, three lots of four and four lots of three are fundamentally different. They think in concrete terms---three children each having four candies are luckier than four children each having three candies although the total number of candies is the same.
（子どもたちにとって，「4が3つ」と「3が4つ」は基本的に別物である．具体物で考えると---4つずつキャンディを持っている3人の子どもは，3つずつキャンディを持っている4人の子どもよりも，運がいい．キャンディの総数は同じなのだけれども．）
(p.157)

Exercises
1. Give some real-life examples of situations in which a multiplication product a×b (for example, 5×6) is not the same as b×a (6×5).
（練習問題．1. a×bとb×a（例えば，5×6と6×5）が同じでないような，日常生活の例を挙げなさい．）
(p.158)

The balance or symmetry in the multiplication square relates to a very important property called the commutative property of multiplication, which states that for any two numbers a and b, a×b＝b×a (for example, 3×4＝4×3). Note that this is a property of numbers. While it is true that 3×4 is equal to 4×3, 3×4 may not be the same as 4×3 in a real-life situation.
（かけ算の表の釣り合いや対称性は，乗法の交換法則と呼ばれる重要な性質に関連している．すなわち，任意の2つの数aおよびbに対して，a×b＝b×aである．例えば3×4＝4×3となる．注意しないといけないのは，これは数の性質ということである．3×4が4×3と等しいのは事実だが，日常生活においてそれらが同じであるというわけではない．）
(p.177)

シュタイナー学校の算数の時間（1995年）

シュタイナー学校の算数の時間

r＝p・a，　あるいは　p・a＝r　　受・能＝結
これによって，2つの因数p,aからなる積が得られます。ここで，pを単位のある大きさ（もちろんrも同時にそうなります）だと考えますと，pとaの違いがはっきりします。例えば，次のようなものです。
12m＝3m＋3m＋3m＋3m
12m＝3m・4
4というのは，同じ値を加える回数です。これは，単位を持つ数であるrやpに対して，純粋な数です。ここでも，結果から見れば因数の交換法則が成り立ちますが，乗法のプロセスに関しては成り立ちません。4m・3＝12mとも，3m・4＝12mともかけますが，角材を切り分ける場合ですと，4mのものが3本と，3mのものが4本とでは，全く違います。
(p.43)

板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉（2003年）

板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉

(p.47)
(p.46)

まるごと2年生 2年生担任が まず読む本（2011年）

まるごと2年生 2年生担任が まず読む本 (教育技術MOOK)

(p.16)

ぐんぐんできる算数練習帳 2年（2011年）

ぐんぐんできる算数練習帳 小学2年 おもしろい問題がいっぱい

絵に　あう　かけ算の　しきを　線で　むすびましょう。

(p.104)

関連：数学教育実践研究会の学習講座に行ってきました | メタメタの日

田中博史の楽しくて力がつく算数授業55の知恵（2011年）

田中博史の楽しくて力がつく算数授業55の知恵―おいしい算数授業レシピ〈2〉 (hito*yume book)

（表）5×8
（裏）
1はこに5こ入りの
チョコレートが
8はこあります。

（表）8×5
（裏）
チョコレートが
5はこあります。
1はこは8こ入りです。

（九九カルタ　文溪堂より）
(p.48)

先生のための学校　計算力が確実に伸びる指導（2012年）

先生のための学校 計算力が確実に伸びる指導 (教育技術MOOK 先生のための学校)

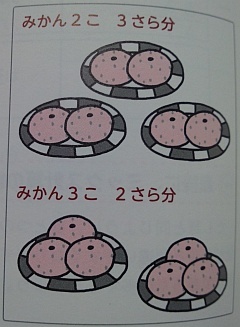
助数詞をつけると理解しやすい

式　2こ×3さら分＝6こ
式　3こ×2さら分＝6こ

これらの答えは6個と同じですが、式にすると全く逆です。
具体的なイメージをつかみにくい場合でも、助数詞（単位）をつける立式の間違いはほとんどなくなります。
このことによって、もとにする量×いくつ分がかけ算だということを理解させることができます。
また、三年生のわり算の学習で、等分除と包含除の違いがわかりやすくなりますし、小数や分数の文章題を習うときにも、この助数詞があることによって、立式の間違いを防ぐことができます。

(pp.22-23)

算数教科書アレンジ事例30（2013年）

10の視点で授業が変わる! 算数教科書アレンジ事例30

(p.34)

補足

上記のいくつかは，今年2月にまとめた資料集（2010〜2011年，2012年〜，外国語文献）からの転載です．
ある場面に対して，「□×△」でも「△×□」でもよいとする事例についても，文献があります．

• アレイ，直積：小学校学習指導要領解説 算数編，『小学算数なっとくワーク2年生』(p.101)，『算数の探険1　たす　ひく　かける　わる（加減乗除）』(p.135)，『板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉』（ふしぎな花のさく木，p.49）
• トランプ配り：『遠山啓著作集数学教育論シリーズ 5 量とはなにか 1 (1978年)』（6×4，4×6論争にひそむ意味），『おかしなおかしな数学者たち (新潮文庫)』（遠山啓/カード式配り方）
• その他：『算数・数学教育つれづれ草』（5円の品3個の代金の立式は「3×5」ではダメなのか），『数とは何か?―1、2、3から無限まで、数を考える13章 (BERET SCIENCE)』（数のかけ算と割り算/かけ算の順序）

□＋△と△＋□は?

加法（たし算）についても，「□＋△」と「△＋□」が違う，あるいは，2つの数が反対になると意味が異なると記しているものがいくつかあります．それらはいずれも，たし算を増加と解釈すれば，「□＋△」と「△＋□」とでは意味が異なる---加法の交換法則を考慮しても---が，合併と解釈すれば，区別はない（同じ）と述べています．
和書では，『数学の自由性 (ちくま学芸文庫)』(pp.75-76)と『数の科学―水道方式の基礎 (1975年) (教育文庫〈7〉)』(p.62)が明快で，朝四暮三にて主要部を引用しています．
海外では，次の文献で，わり算の意味を解説する前に，たし算の意味や解釈について書かれています．

• Ohlsson, S. (1988). Mathematical Meaning and Application Meaning in the Semantics of Fractions and Related Concepts. In Hiebert, J. and Behr, M. (Eds.), Number Concepts and Operations in the Middle Grades, pp.53-92. isbn:0873532651

本文と章末注から該当箇所を取り出し，私訳を添えます．

The referential mappings created by the two concepts of growing and of combining are not identical. When addition is interpreted as growth, the arguments are not interchangeable. Incrementing ten by two is not the same process as incrementing two by ten.5 When addition is interpreted as combining, on the other hand, the arguments are interchangeable. Combining five with three is the same process as combining three with five. In the growth interpretation of addition the first argument and the result both refer to the same quantity, although at different points in time, while in the combining interpretation the two arguments and the result refer to three distinct quantities. Neither the sense not the reference is the same in the two applications (see Figure 1).
（増加と合併という，2つの概念から作られる参照の図式は異なる．たし算を増加と解釈するとき，2つの値（被加数と加数）は交換可能とならない．10に2を加えることは，2に10を加えるのと同じプロセスではない．一方，たし算を合併と解釈すると，2つの値は交換可能となる．5と3を合わせることは，3と5を合わせるのと同じプロセスである．たし算を増加と解釈した場合，最初の値と結果（和）は，時点は異なるが，同じ種類の量を表す．それに対し，合併と解釈した場合には，2つの値と結果はそれぞれ異なる量を表す．増加と合併という，たし算をもとにしたそれら2つの応用（増加と合併）に関して，それらは意味も参照の図式も異なる（図1）．）
(p.59)

5 This fact is sometimes described as a lack of commutativity on the part of the addition function. But the mathematical construct of addition cannot have the property of commutativity in some contexts and lack it in others. Addition is defined to be commutative. But when the addition construct is interpreted as describing growth, (5 + 3) and (3 + 5) refer to two different growth processes. The difference between the two cases resides in the real world, not in the mathematical construct.
（この事実はときには，加法の機能において可換性がないものとして説明される．しかし加法の数学的な構成では，可換性を持つことができない場合や欠落している場合がある．加法は，可換であるように定義される．しかし，加法の構成を，増加を説明するものであると解釈すると，(5 + 3)と(3 + 5)はそれぞれ異なった増加のプロセスとなる．それらの式の違いは，数学的な構成ではなく実生活に内在する．）
(p.92)

追記：p.92について，http://8254.teacup.com/kakezannojunjo/bbs/t21/1054でより明快な訳が書かれています．感謝申し上げます．

（最終更新：2013-06-22 早朝）