何の前触れもない名指しツイートに,びっくりしました.
一連のツイートのうち,@takehikomが口を挟むまでは
- りんごの問題に対して「3こ/まい×5まい」「5まい×3こ/まい」「5こ/かい×3かい」と単位をつけて書けば,それぞれの違いを知ることができる.
を主張したいものと理解しました.後半は,比例と複比例の関連,それと,表におけるそれぞれの値の意味について,確認をお求めということでしょうか.
まず,こちらより言及したVergnaud (1983, 1988)ですが,書誌情報は次のとおりです.
- Vergnaud, G. (1983). Multiplicative Structures, In Lesh, R. and Landau, M. (Eds.), Acquisition of mathematics concepts and processes, Academic Press, pp.127-174. isbn:012444220X
- Vergnaud, G. (1988). Multiplicative Structures. In Hiebert, J. and Behr, M. (Eds.), Number Concepts and Operations in the Middle Grades, Vol.2, pp.141-161. isbn:0873532651
このいずれかまたは両方を引用している,日本語の書籍や文献のうち,見てきたものを挙げておきます.
- 『算数・数学科重要用語300の基礎知識』p.187
- 『数学教育学の成立と展望』p.157
- 『授業に役立つ算数教科書の数学的背景』pp.9-10
- 柏木美穂: 算数・数学学習におけるわり算に関する研究 〜概念領域に焦点を当てて〜, 鳥取大学数学教育研究, Vol.13, No.10 (2011). http://www.rs.tottori-u.ac.jp/mathedu/mathedu/journal13_files/13-10.pdf
- 渡会陽平, 小学校算数科における乗除法の意味に関する学習過程の分析―G. Vergnaudの概念野理論を枠組みとして―, 数学教育学論究 (日本数学教育学会誌臨時増刊), 日本数学教育学会, Vol.97, pp.3-16 (2012). http://ci.nii.ac.jp/naid/110009518193/
ここ以外のブログから1件.といっても本文ではなくコメントです.
なお,VergnaudはWikipedia英語版にエントリがあります([https://en.wikipedia.org/wiki/G%C3%A9rard_Vergnaud]).Vergnaud (1988)のほうは,乗法の構造はこうだというよりも,かけ算・わり算でTheory of Conceptual Fields(概念野理論)を展開するのが中心になっていると理解しています.
ツイートにあったいくつかの疑問に対して,直接答えるというよりは,思ったことを書いていきます.
単位あるいは助数詞の有用性についてですが,「3こ/まい×5まい」「5まい×3こ/まい」「5こ/かい×3かい」といった書き分けは,りんごの文章題に対して,「3×5」あるいは「5×3」という式を書いたとき,教師や大人がどのようにその式を解釈するかを,もっともらしい式に記述したものとなっています.
「もっともらしい」を言い換えると,「算数としては認められていない」です.
算数の答案としては(そして日本では),りんごの文章題で正解となる式は「3×5」だ,というのが,算数教育の主流となっています.
何が主流で何が非主流かを知るには,Web上の情報のみならずいわゆる活字も含めて多読し,自分の頭の中で構築する作業が不可欠です.読むべき情報には,教師らが練り上げた学習指導案や,算数・数学教育の研究者が作成した教師向け解説書,そして出題や解答類型などが載っているテスト問題があります.
古い情報や国外の情報を,取り入れる必要も出てきます.例えば,パー書きの式について書かれた算数教育の英語文献をいくらか,知っていますが,そのように書くよう主張しているのではなく,式の解釈の仕方を述べたものばかりでした.
単位付きの式の解釈の多様性を,Web上で見るにつけ,もっとあるんだけどなあという思いを持っています.実際,りんごの問題に対して「5×3」という式を立てたら,「それだと3枚のお皿に5個ずつになっちゃうよ(5こ/まい×3こ=15こ,5こ×3=15こ)」や「それだとお皿が15枚になっちゃうよ(5まい×3=15まい)」と解釈することができます.子どもがその種の発言をして,5×3はおかしいと展開する授業が多様に見られる一方で,「トランプのように配ると…」を先生が推奨する授業例が見当たらないのは,結局のところここが「ネット談義」と「算数教育の理想像」とのギャップなのかなと感じています.
「(時速)X(時間)の話は,「複比例」として考えることができます.」の件ですが,最初の最初は以下の記述です.
倍指向と積指向の整理《倍の乗法》を《積の乗法》で
次に,上の反対,すなわち《倍の乗法》を《積の乗法》に帰着することを試みます.
- 整数の乗法は,アレイ図で表します.
- 小数や分数を含む場合は,複比例の関係y=a×bまたはy=k×a×b(yはaに比例する.yはbに比例する.aとbは独立である)で表します.
「鉄の重さは銅の0.88倍である.ある銅のかたまりが4.2kgのとき,それと同じ大きさの鉄のかたまりは何kgか?」という,一見,0.88のみが倍率としか見なせない状況でも,「物質Xの重さは銅のa倍である.ある銅のかたまりがb kgのとき,それと同じ大きさの物質Xのかたまりは何kgか?」と一般化すれば,求めるべき重量yは,aにもbにも比例するので,y=a×b=b×aと表せます.
とはいうものの,複比例を小学校で学習する余裕はなさそうです.なので算数教育の改善には寄与の乏しい,大人の議論となります.そのことを前提として,話すのであれば,「まあそういう言い方もできるね」です.
「(質量)=(密度)X(体積)」に関して書かれた思考実験は,「体積を固定すれば,質量は密度に比例する」を示しています.それと別に,「密度を固定すれば,質量は体積に比例する」を確認すれば,「質量は密度と体積に比例する」と言うことができますし,一般に物体の密度と体積は独立ですから,複比例の関係であると言ってよさそうに思うのですが.
Vergnaudの表

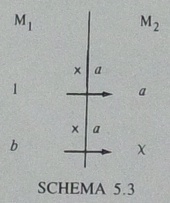
の見方ですが,表に書かれる値の「1」「a」「b」「x」はそれぞれ,ケーキの問題(「1個15セントのケーキを4個買います.いくらになりますか」)に当てはめると,「1個」「15セント」「4個」「60セント」に対応します.
なので,次のような表を得ることができます.
| ケーキ | 値段 |
| 1個 | 15セント |
| 4個 | 60セント |
ですが,表を作る際,単位はできるだけ書くべきではない*1ので,次のようにしたいところです.
| ケーキ(個) | 値段(セント) |
| 1 | 15 |
| 4 | 60 |
縦に見る関係,横に見る関係の解釈ですが,まず「b=4個/1個=4個/個=4×1=4」に関して,意図は分かるけれども自分なら「b=4個/1個=4」とします.また「図中の1を1個ではなく純粋数の1と捉え」るのには賛同できません.それは1と4が同じ量空間の要素であることに反するからです.
その一方で,矢印に添えられる文字・数量は,表の制約を受けません.SCHEMA 5.2のbは無次元量の「4」,SCHEMA 5.3のaは,2つの量空間の次元を考慮して「15セント/個」としても,不具合はなさそうです.