2.3×5 - わさっきhb

ざっと読んで，まず思い浮かんだのは「ドン・キホーテ」．企業じゃなくてwikipedia:ドン・キホーテのほうです．
それはさておき，本日取り上げたいのは次の箇所です．

ところが、こうするとややこしいことが起こってしまうのだ。現在の学習指導要領では、「小数×整数」と「整数×小数」を別の学年で学ぶことになっている。どういうことかというと、1ｍの重さが2.3ｇの針金5ｍ分の重さを求める計算と、1ｍの重さが5ｇの針金2.3ｇ分の重さを求める計算は、別の計算であると考えている。学年をまたぐことはおいといて、このこと自体はしごく妥当なことだと私は思う。
教科書の問題点は教科書会社に意見を出していく。（並行して文科省にも）｜tamami_tata｜note

http://kodomo.artet.net/?eid=1229006も合わせて読んだのですが，なぜ「別の計算である」かが，記されていません．
あえて推測するなら，「小数×整数」は4年で，「整数×小数」は5年で学習することが，学習指導要領に書かれているからだ，といったところでしょうか．
学習指導要領解説から，根拠を見ておくと，「×整数」は累加で計算ができます．視覚的・操作的にも，「何のいくつ分」で表現できます．昨年，wikipedia:かけ算の順序問題の改訂に携わった際，「0.1 × 3ならば、0.1 + 0.1 + 0.1の意味である」を入れましたが，これは学習指導要領解説から取ってきたものです．被乗数にあたるほうは分数でもかまいません．
これと比較すると，「整数×小数」や「小数×小数」は，「何のいくら分」と表せます．計算という観点でも，小数というのが1未満であっても，1より大きい値であっても，累加で計算ができなくなります（乗法の意味の拡張）．
海外文献と照合することで，さらに違いを見ていくことができます．

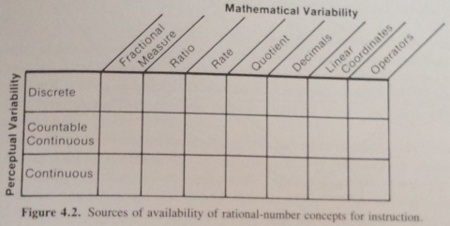
事情により出典は手短に：isbn:012444220Xのp.101です．
表の各行，「Discrete」は分離量，またはそれを数に対応させたものです．「Continuous」は連続量です．「Countable Continuous」は，数えられる連続量となります．ここまで書いてきた中でいうと，5ｍや5ｇは，数えられる連続量です．これが乗数となるようなかけ算もまた，累加で計算ができるというわけです．
学習指導要領解説に戻りまして，小数のかけ算を扱うより前，第3学年に，「１ｍのねだんが85円のリボンを25ｍ買うと代金はいくらか。」というのが書かれています．このうち，25ｍは数えられる連続量です．したがって累加で計算するなり，1ｍを25個分かいた図を作ったりできるわけですが，精密な図にしなくても，場面を認識でき，計算できることがそこでは期待されています．
「１メートルの長さが80円の布を2.5メートル買ったときの代金が何円になるか」となったとき，長さは「数えられる連続量」でなくなり，連続量として扱うような学習となっています．