目次
- 1. 累加そして拡張
- 2. 非累加
- 3. 英語文献に見る累加
- 4. 小数×整数も,累加と拡張
- 5. 割合の場面
- 6. なぜ「小数×整数」を,小数の乗法より先行して学ぶのか
- これまで書いてきたこと
1. 累加そして拡張
小学校の算数における乗法(かけ算)の指導について,「通説」と言っていいものがあります.それは,まず累加(例えば2×5=2+2+2+2+2)によって乗法の意味づけを行い,累加で意味づけられなくなる段階,具体的には乗数が小数となるような場面において,乗法の意味の拡張を図るというものです.
この考え方に基づく記述を,いくつか取り上げます.
【整数の乗法と除法】
第2学年では,乗法が用いられる場合や計算の意味について理解できるようにする。例えば,一つ分の大きさを知ってその幾つ分か,または何倍かの大きさを求める計算として意味付けをしたり,同数累加(加法の繰り返し)によって,その結果を求めたりする。第2学年では,乗法九九を知り,1位数と1位数の乗法を確実にできるようにすることが特に重要である。なお,乗法九九の理解を深めるために,簡単な場合の2位数と1位数との乗法も扱う。
(略)
【小数の乗法と除法】
第4学年では,乗数や除数が整数である場合の小数の乗法及び除法の計算の仕方を考え,それらの計算ができるようにする。
第5学年では,乗数や除数が小数である場合の乗法及び除法を用いることができるようにする。乗数が小数である計算になると,加法の繰り返しという累加の意味ではとらえられなくなるので,計算の意味を広げる必要がある。除数が小数である計算についても,計算の意味を広げる必要がある。
(『小学校学習指導要領解説 算数編』p.38; http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_1.pdf#page=41)
これらの研究成果から,乗法・除法の意味づけにおいては,数学的な考え方の育成を目指す立場からは,割合による意味づけに教育的な価値がある。これは,整数は同数累加で導入し,乗数が小数になった段階で同数累加では意味づけられなくなる。そこで,被乗数,乗数の意味を(基準量)×(割合)と拡張し,これまでの整数の場合と同様に用いることができるようにすることである。数学的な考え方を育成するためには,意味の拡張は重要な指導の場となってくる。
(『数学教育学研究ハンドブック』pp.74-75)
a) 乗法を累加の考えで指導することについて
累加の考えをさけようというのは,算数の指導についての基本的な立場の相異によることであって,乗法という問題だけで考察することは適切とはいえない.(略)しかし,乗法と加法の特別な場合を簡潔に表すという立場から意味づけることは,とくに,低学年の場合には,教育的にも意味のあることであり,さきのラパッポルト氏の反論にもある.
わが国でもこの立場をとっているが,アメリカの新しい計画による教科書でも,この立場をとっているものが多い.これには,ラパッポルト氏の指摘にもあるように,整数の段階では,集合の直積に近い意味づけをしても,累加の考えに帰著してほぼ処理できることや,直積の考えのままでは,実際に乗法を適用するに当たって,困難をともなうことなどの理由があげられよう.
b) 小数・分数(有理数)の場合に,どんな意味づけをするか.
累加の考えの問題点は,周知のように,整数の場合ではなく,乗数が有理数の際に起こる.わが国の場合は,累加という考えをそのまま用いないで,次のような意味に一般化(拡張)する方法をとっている.すなわち,
A×Bについて,A,Bを次の意味に対応させる.下の図では,A×Bは,Bの目盛に対応する大きさをよみとることに当たる.
A……基準(単位)とする大きさ
B……Aを単位とした測定数(measure)
(中島健三: 乗法の意味についての論争と問題点についての考察. http://ci.nii.ac.jp/naid/110003849391)
2. 非累加
累加そして拡張とはまた別の,乗法の指導法もあります.「1あたり×いくつ分」と書くことができます.書籍だと『量の世界―構造主義的分析 (1975年) (教育文庫〈8〉)』や『子どものつまずきと授業づくり―わかる算数をめざして (子どもと教育)』,論文ならhttp://ci.nii.ac.jp/naid/110008729855で,その詳細を知ることができます.
なのですが,算数教育を見ていく上で,知っておく価値はあるものの,個人的にこのアプローチは必ずしも良いとは思っていません.
その理由を4点,挙げます.まず,「1あたり」の概念を---たとえ「1あたりの数」という分離量であっても---,かけ算の学習時(2年の児童ら)に身につけさせるのが,困難となります.本を開いても,次のように指摘がなされています.
一方,意味の拡張を意図しない立場では,乗法の意味づけは,(内包量)×(外延量)になる。乗数を外延量とすることで,整数でも小数でも意味づけは変わらないことになる。
この意味づけの課題は,乗法の導入段階で内包量の見方を児童ができるかということである。例えば,みかんが3こある場面で,これを3こ/皿という内包量として見るのは児童にとって難しいことである。また,数学的な考え方と関わった意味の拡張などの見方をどのように扱うかを明らかにする必要がある。
(『数学教育学研究ハンドブック』p.75)
(1当たり量)×(いくら分)については,その背後に量×量といった理論があって,これだけではその意をつくしてはいない.しかし,これ以上述べていく余裕もないので,うさぎや象などを材料にして(1当たり量)×(いくら分)で整数のかけ算の意味づけがなされていることにとどめておきたい.
(略)
このような場合に何に留意していかなければならないかといえば,子どもの理論に即した問題設定があり得るかどうかということである.この観点でbとcの立場の指導の方向性を考えると,cの立場に,かなり無理があるような気がしてならない.第一に「1当たり量」の必要性が果たして理解され得るものかどうか.“うさぎ1匹あたり耳2本”“象1頭あたり足4本”といっても,あまりにもあたりまえすぎて,なぜこのような表現をとらなければならないのかその目的意識が子どもに理解できにくい.第2に,cの立場では,かけ算と累加を切り離すために,答えの求め方はどんな方法でもよいとして,例えば,8×5の答えなどをタイルを用いて右図のような方法で見つけさせようとしている.果たして,8×5の答えをこのような方法で見つけていくのが自然であるのかどうか.
さらには,2×0を「うさぎが一匹もいません.うさぎの耳は何本ですか」といった問題場面での中でとらえさせようとしているが,問題場面そのものが無意味であり問題化されにくい.
(手島勝朗: かけ算の意味と方法の具体的展開 -整数のかけ算-. 『整数の計算 (リーディングス 新しい算数研究)』p.114)
次に,加法と乗法を切り離す方針のため,かけ算の指導が,「1あたり」の学習からとなっています.それに対し,学習指導要領ほかから読み取れる,かけ算の指導は,いわゆる3口のたし算(明らかに,累加の基礎です)のほか,「まとめて数える」「2ずつ,5ずつ,10ずつ」が素地となっています.いずれも1年で学習します.また2年で乗法を学習する中でも,「乗数が1ずつ増えるときの積の増え方」,具体的には「乗数が1増えれば積は被乗数分だけ増えるという性質」*1は,意味においても計算においても知っておくと良い事柄ですが,「1あたり」に基づく指導法では,これらへの配慮が見当たりません.
3番目に,結合法則の学習で,1あたり量どうしのかけ算が発生します.例えば90円/個×3個/箱×2箱という式を立て,計算するとき,90円/個×3個/箱=270円/箱によって1個あたりの金額から1箱あたりの金額に変換できるのですが,被乗数・乗数・積がいずれもパー書きの量となるのは,3年向けとは思えません.ここで結合法則は一例であり,より一般には,答えを得るのに複数の演算を使用する状況において*2,数の部分を維持したまま,内包量から外延量へ(またはその逆),明示的あるいは暗黙による変換が必要な状況があります.『かけ算とわり算 (わかって楽しい算数教室 1)』では,わり算は等分除のみとし,それぞれの答えにはパー書きの単位が添えられているところ,ある例だけ(pp.81-82),「183個÷3=61個」「183個÷3+140個÷4=61個+35個=96個」と,等分除だけれども(たし算ができるようにするため)パー書きを書いていない箇所があります.
最後に,「1あたり×いくつ分」のスタイルの推進にあたり,累加だと乗数が小数・分数になったときに対処できないと指摘している点です.「累加」だけを見て「拡張」を無視している,と言ってもいいでしょう.世界はどうなっているのかというと,累加に関する海外の論争を踏まえ,累加と拡張に基づく「わが国の立場」の解説(提案ではなく)が,前述の中島の文献により,したがって1960年代に記されています*3.「累加だと乗数が小数・分数になったときに対処できない」のは十分承知の上で,それで小数・分数でも使える(立式・計算できる)ようにどのように学習内容を配列し,また授業で指導していけばよいかが,検討され実践され,そして確立されています.「1あたり」から始まる乗法の意味づけは,そういった算数教育の継続性を,断ち切ろうとしているように見えます.
累加そして拡張を「通説」と呼んだのに対し,1あたりあるいは非累加に基づく指導は,出版物や実践事例も相当にあることから,「有力説」と呼んでよさそうです.通説に肩を並べようとするのなら,「1あたり」の意味づけに基づく検定教科書を発行する*4ことが,そのマイルストーンとなるのではないでしょうか.
3. 英語文献に見る累加
先ほど「世界はどうなっているのかというと」と書きましたが,そのあとに記したのは国内事情ばかりでした.海外文献に目を向けます.
- Bell, A., Fischbein, E. and Greer, B. (1984). Choice of operation in verbal arithmetic problems: the effects of number size, problem structure and context. Educational Studies in Mathematics, Volume 15, Issue 2, pp.129-147. http://link.springer.com/article/10.1007/BF00305893
Calculator experience can thus help to eradicate the misconceptions, and as its use in the primary school becomes more extensive, it should diminish the tendency for them to arise. However, this still leaves the question of what meanings the pupils can attach to the operations. For 6 × 4, it is easy to think of 6 lots of 4 objects (repeated addition), and this can be extended to include repeated addition of measures (e.g. 6 lengths of string each 4.1 metres long). To find a situation modelled by 6.2 × 4.1, however, one has to go to a conceptually very different context, such as the area of a rectangle, unit price × quantity, speed × time, or enlargement.
(私訳:したがって電卓使用の経験ははそのミスコンセプションをなくすことに役立ち,小学校での電卓の使用がより広範囲になるにつれて,そういったミスコンセプションが発生する傾向を減少させることになればよい.しかしながら,そのようにしたとしても,生徒らが操作にどのような意味を付与することができるのかという問題は依然として残っている.「6×4」という式に対して,4個のものが6組ある(累加)と考えるのは容易だし,これを量の累加に拡張することもできる(例えば,4.1メートルの紐の6本分の長さ).しかしながら,6.2×4.1でモデル化される場面を見つけるには,長方形の面積や,単価×個数,速さ×時間,あるいは拡大といった,概念的に大きく異なる文脈を用意しなければならない.)
(p.130)
この文献の全体像は,おおよそ次のとおりです.小数のかけ算やわり算の意味理解に関する調査を行っています.かけ算についてはRepeated addition, Rate, Measure conversion, Enlargementといった何種類かのタイプ(Type)に基づく文章題で,式を答えるほか,式から文章題を作るという出題もあります.タイプもさることながら,被乗数・乗数にあたる数の種類に配慮がなされています.結果としては,正解式が1.33×0.53や2×0.14となる,純小数が乗数となる場面の正解者数が,他よりも低くなっています.
上記引用のミスコンセプションは,前のページに書かれていまして,「わり算は大きな数を小さな数で割る」「かけ算をするとその結果はかけられる数よりも大きくなる」があります.その後,国内において(http://ci.nii.ac.jp/naid/110006184927),1より小さい数を乗数とする演算が,他の種類のかけ算よりも間違えやすいことは,文章問題においても計算問題においても存在することが指摘されています.
この文献は「調査」が主眼となっており,そういった出題タイプごとの正解率の違いに注意して,どのようなやり方で小数のかけ算・わり算の学習をすればいいのかについては,読み取れませんでした.
とはいえ,どこまでは累加で差し支えなく,どうなると累加では都合が悪いかについては,日本の算数教育と同じとなっています.「量の累加(repeated addition of measures)」というのが大事なところで,連続量×分離量,あるいは4.1×6で表される場面は,累加で求められるわけです.
また別の文献を見ます.学術論文ではなく,“Help Your Kids With Maths”という,親子で読める本です.そこでは,4行3列に並んだ人の総数を,「4×3=3+3+3」と「3×4=4+4+4+4」の2通りで表しています(p.19).
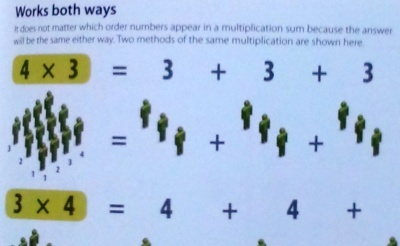
これには和訳された本もあります.『親子で学ぶ数学図鑑:基礎からわかるビジュアルガイド』です.同じp.19では,同じ状況に対して「3×4=3+3+3+3」と「4×3=4+4+4」という式を用いています.日本人読者向けの配慮,でしょうか.

4. 小数×整数も,累加と拡張
さて日本の算数に戻りましょう.被乗数が小数,乗数が整数となるようなかけ算を,乗数が小数のかけ算と区別して意味づけを図るのは,現在のカリキュラムのもとでは4年で扱われています.意味あるいは「かけ算で求められると判断する根拠」には,累加を用います.ジュースのような,手軽に用意できて足し合わせることができるものが,導入によく用いられます.
鳥取大学の学生らの調査(http://www.rs.tottori-u.ac.jp/mathedu/mt/xue_sheng_zuo_pin_files/2012_DmI%26DdI.pdf)によると,学校図書の算数教科書について,小数×整数の最初の例題は,「□Lずつ入っているジュースのびんが,3本あります。ジュースは全部で何Lあるでしょうか」で,□にまず2や3,その後1.2を入れることで,1.2×3という式を得ています.「1mの重さが2.3gのはり金があります。このはり金4mの重さは何gでしょうか。」はその後の例題です.
ここでジュースの問題は,上述のとおり実際に操作(足し合わせて総量を確認)しやすいほか,0.1L=1dLを単位としてそれがいくつあるかによって求めらます.それに対し,はり金の問題では,「1mの重さが2.3gである」「4mなら(重さを量ると)9.2gである」「針金は均質である(ある1mは2.3gだけれど,別の1mは2.1gだった,ということがない)」と,量の扱いにおいて要注意ですし,「0.1g」を単位とすることの必然性が薄れます.
ジュースの問題は,はり金の問題よりも,「小数×整数」の導入に適しています.一方,はり金の問題はそれより後で,具体物を用意しなくてもかけ算と判断し,計算するための教材とするのがよさそうです.
『小学校算数 板書で見る全単元・全時間の授業のすべて 4年〈下〉』も,同様の流れをとっています.小数のかけ算の授業・板書例はp.98から始まります.最初の出題は,「□Lずつのジュースが4本あります。全部で何Lでしょう」です.その後,「2.3L入りのバケツが4こあります。水は全部で何L入るでしょう」(p.100),「1.6mのテープを34本作るには,テープは何m必要ですか」(p.102)までは量の累加です.その次の「1mが1.45kgのパイプがあります。このパイプ7mの重さは何kgですか」(p.104)はというと,量の累加で求められるものの,1.45kg/m×7mと考えることのできる場面となっています.
導入は被乗数・乗数とも「小数×整数」の範囲で簡単な数を採用し,授業を進めるにつれて,乗数が大きな数になったり,被乗数が小数第2位にまで及んだりしていきながら,実物の操作や計量をすることなく,かけ算で答えが求められるようになっています.これもまた「拡張」です.
5. 割合の場面
前節で「1.45kg/m×7m」と書きました.これは「1あたり×いくら分」に基づく立式です.実際,7mは計算の都合であり,4年で学ぶのは「小数×整数」だからそれに合わせたまでと見ることもできますが,Bellら(1984)に書かれている,以下の記述と整合します.
A more complex group of situations involving multiplication and division we will refer to collectively as rate structures. These include questions relating to speed, price, miles per gallon, etc. Other applications generally encountered in school are rectangular area, measure conversion, and enlargement, in classifying these, we emphasize differences in structure (particularly repeated addition versus the rest for multiplication, and partition, quotition and rate for division), and differences in context. *5
(私訳:かけ算およびわり算に関する,もっと複雑な場面として,「割合」が挙げられる.割合には,速さ,価格,燃費(ガロンあたりの走行マイル)などが含まれる.学校で学ぶ他の(かけ算やわり算の)応用には,長方形の面積,単位の換算,拡大があり,それらを分類するにあたって,構造上の違い(特に,かけ算においては累加とそれ以外,わり算に関しては等分除・包含除と割合の間で)と場面の違いを重視したい.)
(p.130)
共著者の一人Greerは,『Handbook of Research on Mathematics Teaching and Learning: (A Project of the National Council of Teachers of Mathematics)』の中で,かけ算・わり算の分類表を載せています(https://books.google.co.jp/books?id=N_wnDwAAQBAJ&lpg=PR1&hl=ja&pg=PA280#v=onepage&q&f=false).そこでも,割合(Rate)の例としてボートの速さの計算を挙げています.
「1mの重さが2.3gのはり金があります。このはり金4mの重さは何gでしょうか」や「1mが1.45kgのパイプがあります。このパイプ7mの重さは何kgですか」は,小数×整数で求めることができる,「割合」の場面となっています*6.
ところで,我々が「割合」というと,2分の1だとか5割だとか50%だとかいったものを,思い浮かべがちですが,それについては部分と全体(Part/whole)という分類名を与えています.
(2021年8月追記)
- ここの「割合」は,小学校学習指導要領の算数では「異種の二つの量の割合」や「単位量当たりの大きさ」と表記される概念と重なります。
- Bellら(1984)に書かれた"speed, price, miles per gallon"について,"speed, unit price, miles per gallon"と読み替えることで,いずれも「1あたり」であることがより明確になります.
- 「割合」「Rate」「1あたり」の考え方や,日本の算数での指導などについては,以下にて取りまとめました.
6. なぜ「小数×整数」を,小数の乗法より先行して学ぶのか
「小数×整数」を,小数の乗法の最初に指導することの意義として,以下の点を挙げ,本記事の結論とします.
- 累加で計算できる.
- 適当な被乗数・乗数であれば,総量を求める操作を実際に行える.
- 値や場面を変えていき,実物がなくても計算で求められるような指導がしやすい.
- 割合(Rate)のうち,乗数が整数となるような場面にも適用できる.
これまで書いてきたこと
*1:「具体的には」の直前は学習指導要領に,直後は『小学校学習指導要領解説 算数編』に,それぞれ書かれています.
*2:算数教育の用語としては「3要素2段階」や「総合式」が関連します.
*3:また「(ぜんたいのねだん)=(ひとつのねだん)×(買ったかず)」という,累加に依拠しない乗法の言葉の式が,昭和33年(1958年)の学習指導要領に見られます.
*4:学習指導要領や解説の改訂があっても,いいでしょう.「1あたり」を「かけ算には順序がない」に置き換えまして,算数教育の系統性をきちんと配慮してきていないのが,透けて見えるような言明に出くわしたとき,「ネットde真実」を思い浮かべるのです.
*5:以下略としますが,直後の文でVergnaud (1980)という文献を引用し比較しています.この文献の標題は'Didactics and acquisition of "multiplicative structures" in secondary schools'です.参考文献には,同じ著者がその前年に書いた'Acquisition des "Structures Multiplicatives" dans le Premier Cycle du Second Degre'というのも入っています.Vergnaudは「乗法構造」についてまずフランス語で執筆し,その後,英文にしたものと思われます.
*6:『小学校学習指導要領解説 算数編』では,「1mのねだんが85円のリボンを25m買うと代金はいくらか」を第3学年の内容として例示しています.整数×整数(2位数どうしのかけ算)ですが,これも「割合」と見ることができます.