3つの数のかけ算を，無向グラフできれいに表示したい

　『東大の先生! 文系の私に超わかりやすく算数を教えてください!』のp.109には，交換法則の説明と，等式が書かれています．
　等式は，2つの文字の間では「A×B＝B×A」，3つの文字の間では「（A×B）×C＝C×（B×A)〔ここで改行〕＝C×（A×B）」です．
　3つの異なる文字（または数）のかけ算は，（A×B）×CとA×（B×C)を異なる式と考えると，全部で12個あります．「異なる式」と書きましたが，それらは乗法の交換法則と結合法則により，等号で結ばれます．
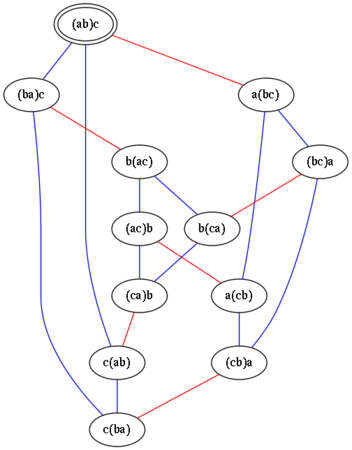
　12個の式のあいだで，交換法則・結合法則が適用できる式を結んで有向グラフを描くことは，2016年に実施していました．

交換法則・結合法則で探索2

それから，少し修正して，Graphvizの入力となるDOTファイルを生成してみました．変換プログラムとDOTファイルは非公開とします．因数の数が3で，(ab)cの式を起点としたとき，交換法則・結合法則を適用して得られる式の関係は以下のようになります．

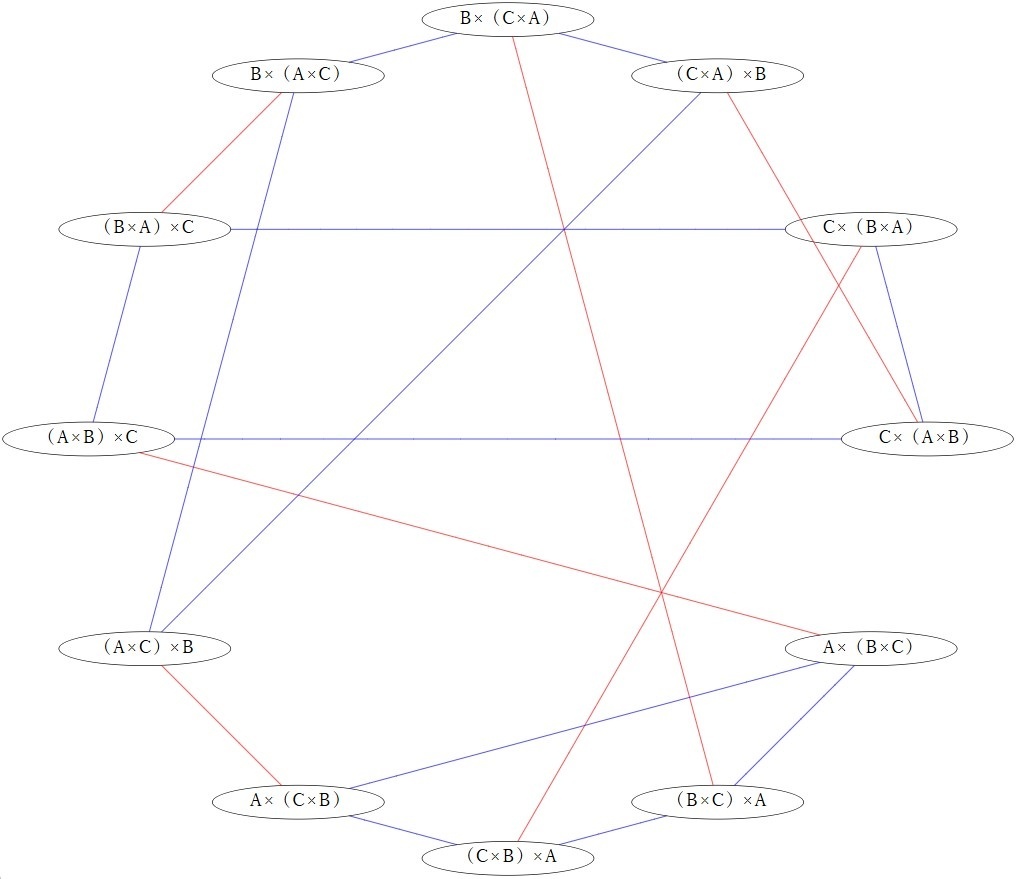
　しかし12個の式が，きれいに配置されていません．これについて，dotコマンドで試行錯誤してみると，-Kcircoというオプションによる"circular layout"*1が分かりやすい表示に見えました．
　2016年のときは「(ab)c」を起点としていましたが，冒頭の本の「（Ａ×Ｂ）×Ｃ」に対応しますし，これを他の（3つの文字の）かけ算の式と区別する必要はありません．dotファイル(ABC.dot)は次のようになりました．

graph abc {
  node [fontsize="25pt"];

  AB_C [label="（Ａ×Ｂ）×Ｃ"];
  BA_C [label="（Ｂ×Ａ）×Ｃ"];
  C_BA [label="Ｃ×（Ｂ×Ａ）"];
  C_AB [label="Ｃ×（Ａ×Ｂ）"];

  BC_A [label="（Ｂ×Ｃ）×Ａ"];
  CB_A [label="（Ｃ×Ｂ）×Ａ"];
  A_CB [label="Ａ×（Ｃ×Ｂ）"];
  A_BC [label="Ａ×（Ｂ×Ｃ）"];

  CA_B [label="（Ｃ×Ａ）×Ｂ"];
  AC_B [label="（Ａ×Ｃ）×Ｂ"];
  B_AC [label="Ｂ×（Ａ×Ｃ）"];
  B_CA [label="Ｂ×（Ｃ×Ａ）"];

  AB_C -- BA_C [color = blue];
  C_BA -- C_AB [color = blue];
  AB_C -- C_AB [color = blue];
  BA_C -- C_BA [color = blue];

  BC_A -- CB_A [color = blue];
  A_CB -- A_BC [color = blue];
  BC_A -- A_BC [color = blue];
  CB_A -- A_CB [color = blue];

  CA_B -- AC_B [color = blue];
  B_AC -- B_CA [color = blue];
  CA_B -- B_CA [color = blue];
  AC_B -- B_AC [color = blue];

  AB_C -- A_BC [color = red];
  BC_A -- B_CA [color = red];
  CA_B -- C_AB [color = red];

  CB_A -- C_BA [color = red];
  BA_C -- B_AC [color = red];
  AC_B -- A_CB [color = red];
}

　dotコマンドが利用可能な環境で，dot -Kcirco -Tsvg ABC.dot > ABC.svgを実行し，ABC.svgをブラウザで見ると…