昨日の件の続報です.公開したRubyスクリプトにいくつか思い違い(論理エラー)があり,デバッグしました.ソースは昨日と同じgistよりご覧ください.
修正した結果,引数指定なしの出力の最終行は「4 factors: 120 expressions / 180 commutative / 120 associative」となりました.交換可能,結合可能な式のペアがそれぞれ半減しています.また因数の数が8の場合にも,約半日かかって出力が出ました(値は,後ろにつけた表をご覧ください).
それから,少し修正して,Graphvizの入力となるDOTファイルを生成してみました.変換プログラムとDOTファイルは非公開とします.因数の数が3で,(ab)cの式を起点としたとき,交換法則・結合法則を適用して得られる式の関係は以下のようになります.
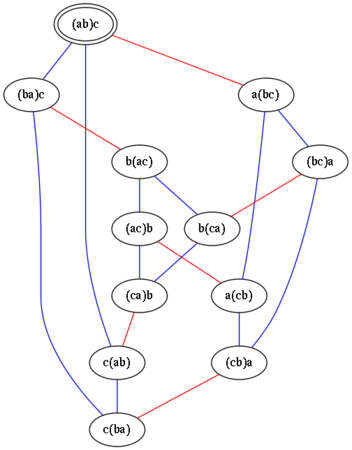
ここで青線は交換可能な式どうし,赤線は結合可能な式どうしを結んでいます.どの式にの節点からも,青線2つと赤線1つが出ています.青線だけで見ると,4つの式を環状に結んだグループ*1が3つという構成です.その各グループが,赤線でつながっています.
因数の数を4としたときの図も,作ってみました.どの式の節点からも,青線3つと赤線2つが出ています.青線だけで見ると,8つの式の節点で立方体が構成される,15個のグループに分割されます.赤線だけで見ると,5つの式による環状グループが24個です.「立方体」を出力するには,((ab)c)dを起点とし,交換法則のみを適用して得られる式に限定すればよく,以下の図になります.

因数の数を変えて得られる数からも,規則性を見ることができます.まずは因数の数を1から8にして得られる,出力の最終行を,表にします.あとの説明のため,因数の数がnのときに,得られる式の数をe(n),交換可能な等式の数をc(n),結合可能な等式の数をc(n)と書きます.
| 因数:n | 式:e(n) | 交換可能:c(n) | 結合可能:a(n) |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 2 | 1 | 0 |
| 3 | 12 | 12 | 6 |
| 4 | 120 | 180 | 120 |
| 5 | 1680 | 3360 | 2520 |
| 6 | 30240 | 75600 | 60480 |
| 7 | 665280 | 1995840 | 1663200 |
| 8 | 17297280 | 60540480 | 51891840 |
このとき,e(n)/e(n-1)は,以下のとおり等差数列になります.bcコマンドで2*6*10*14*18*22*26を計算させると,17297280になることも確認しました.
| n | e(n) | e(n)/e(n-1) |
|---|---|---|
| 1 | 1 | ― |
| 2 | 2 | 2 |
| 3 | 12 | 6 |
| 4 | 120 | 10 |
| 5 | 1680 | 14 |
| 6 | 30240 | 18 |
| 7 | 665280 | 22 |
| 8 | 17297280 | 26 |
またc(n)/e(n),a(n)/e(n)も,それぞれ等比数列です.
| n | e(n) | c(n) | a(n) | c(n)/e(n) | a(n)/e(n) |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 2 | 1 | 0 | 0.5 | 0 |
| 3 | 12 | 12 | 6 | 1 | 0.5 |
| 4 | 120 | 180 | 120 | 1.5 | 1 |
| 5 | 1680 | 3360 | 2520 | 2 | 1.5 |
| 6 | 30240 | 75600 | 60480 | 2.5 | 2 |
| 7 | 665280 | 1995840 | 1663200 | 3 | 2.5 |
| 8 | 17297280 | 60540480 | 51891840 | 3.5 | 3 |
ともに公差は0.5ですが,a(n)/e(n)はc(n)/e(n)より1行ずつ,後ろになっています.因数の数を増やしていっても,交換可能な式のペアのほうが常に,結合可能な式のペアよりも大きくなることを,示唆しています.
ここまで書いた比について,n,および/または,式の構成に関する帰納法で証明できそうですが,そこまで手が回りません.
*1:例えば(ab)cとc(ba)は,直接結ばれていませんが,同じグループです.というのも,交換法則を2回適用すると,一方から他方の式が得られるからです.