幅の違う2本のテープを重ねたとき,その共通部分は,平行四角形です(向かい合った2組の辺がそれぞれ平行です).ただし直角に交わったときには,長方形になります.
このとき,次のどちらが正しいでしょうか?
- 2本のテープの幅に応じて,角度をうまく選べば,ひし形を作ることができる.
- どのように重ねても(交わる角度によらず),ひし形を作ることができない.
三角比(三角関数)を使用することなく,「ひし形を作ることができない」を証明できることに気づきました.
2本のテープのなす角が90°でないとき(90°のときは(正方形でない)長方形になります),共通部分の平行四辺形ABCDについて,下図のように,∠Bが鋭角になるよう定めます.
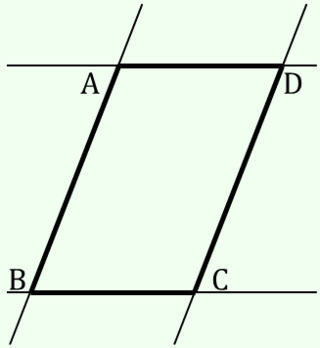
Aから直線BCに下ろした足をEとします*1.
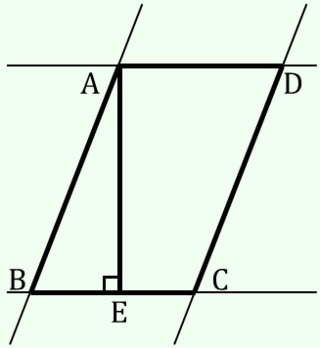
Cから直線ABに下ろした足をFとします.

このとき,△ABE∽△CBFです.なぜなら,∠ABE=∠CBF(∠Bは共通),∠AEB=∠CFB=90°であり,2つの対応する角の大きさがそれぞれ等しいからです.
2つの三角形が相似ということで,対応する辺の長さの比が等しくなりますので,=
です.
ここで,AEとCFは,2本のテープの幅を表します.もしAE=CFならば,先ほどの,対応する辺の長さの等式の値は1となり,AB=CBです.
しかしAE≠CFなので,AB≠CBです.以上より,四角形ABCDはひし形となることはありません.(証明終)
上記のうち,Bを鋭角になるようにとったのは,証明を簡単にする(場合分けを減らす)ためです.Bが鈍角のときに,同じように2点E,Fをとることができますが,図は以下のようになります.

ですがこの場合でも△ABE∽△CBFは成立し,辺の長さの比の等式も同様です.相似条件に関して,∠ABE=∠CBFは,∠Bが共通であることではなく,対頂角が等しいことによって示されます.
ということで,中学で学習する,「図形の相似」*2を使用して,「ひし形を作ることができない」のを説明してきました.ただし「AE≠CFなので,AB≠CB」のところは,中学数学では難しい内容のように思います.
もとの問題は小学校第4学年での出題です.ひし形にならないことについては,ここまで書いてきた論証ではなく,2本のテープの幅と,なす角を,さまざまに変えて,共通部分となる図形の4辺(のうち隣り合う2辺)を測定*3して表に整理し,テープの幅が異なるときには,どのような角度でも2辺の長さが等しくならないことを確認するのが一つの手段です*4.
*1:Eが線分(平行四辺形の辺)BC上にあるとは限りません.テープの幅や,なす角の大きさによっては,線分BCの外となる場合もあります.Fについても同様です.
*2:https://w3id.org/jp-cos/8350233210000000
*3:平行四辺形の頂点の一つの角が30°のとき,上の証明の△ABEや△CBFが,正三角形の半分の形であることから,平行四辺形の辺の長さは,テープの幅のちょうど2倍となることが言えますが,このことを活用した,全国学力テストの小学校算数での出題は,難しそうです.また図形の相似は,中学校第3学年の学習ですので,第2学年までの学習内容に基づく全国学力テストの中学校数学でも,出しにくいと言えます.
*4:https://tosanken.main.jp/data/jittaityousa-kousatu/h25gakuryokujittaityousa/H25gradeall.pdf#page=8の解説には,「ひし形について学習する際、実際に4つの辺の長さを測ったり、コンパスを使って辺の長さに着目して作図したりする活動を通して、「全部の辺の長さが等しい四角形」であるという定義の理解を確実にしたい。また、実際に幅のちがう2本のテープを動かす活動を取り入れ、平行四辺形や長方形ができる理由を問うことで、根拠をもって図形を決定できるようにさせることが大切である。」と書かれています.