本当はプログラムコードの考察をしたかったのですが,ここ数日,気力がないので,軽い話をします.
2次元座標平面の原点からスタートして,第1象限とX軸・Y軸の各格子点を順に巡るというプログラムを,いくつか作ることにしました.
尺取り虫プログラム - わさっき
(略)
理論的には,自然数の集合N={0,1,2,...}と,N×N={(x,y)|x∈N,y∈N}とが一対一対応になるというものです.
上に引用したことだけであれば,尺取り虫のような形状だけでなく,いくつか考えられます.ひとつめ.

この図の経路では,座標(x,y)とステップ数nの関係が,という式で表されます.
簡単に理由を書くと,X軸上の各点とnとの対応は,(0,0)が0,(1,0)が1,(2,0)が3,(3,0)が6,…なので,(X,0)にはが対応します.与えられた座標P(x,y)に対して,座標Q(x+y,0)を考えると,X=x+yですから,Qのステップ数は
です.そしてPは,Qのちょうどyステップあとなので,yを加えれば,欲しい結果となります.
ふたつめ.
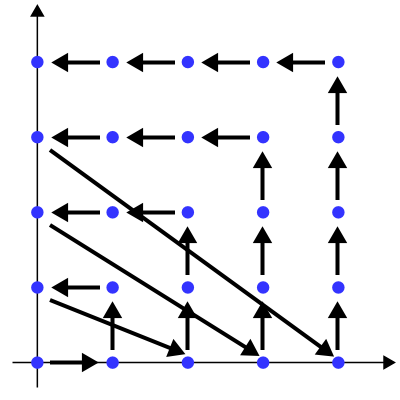
形状ですが,先のほうはまだ尺取り虫に見えると言えば見えますが,これはもはやそうではなく,渦巻き型,あるいはヤドカリの貝の形になっています.
上にあげた2つの図(の経路)のほうが,座標とステップ数の対応を計算しやすく,なのでわざわざ構造体に格納だとかしなくても,xとyの値を指定すれば,何ステップでそこに行けるかが,求められそうです.
計算という面では簡潔でいいのかもしれませんが,しかし上のいずれの経路も,「次の位置」が大きく飛ぶところがある,という点で,形状の美しさは劣るように思えます.
プログラムを書いた経路は,上,左上,右,右下の4種類,もう少し厳密に書くなら(0,+1), (-1,+1), (+1,0), (+1,-1)という4つの「増分」処理だけで,N×N={(x,y)|x∈N,y∈N}のすべての点を順にたどることができることを,示しています.
そこでさらに,斜めを消して,上下左右,すなわち(0,+1), (0,-1), (-1,0), (+1,0)の増分だけで,飛躍なく,漏れなく重複なく,各点を通れるか,考えてみました.図はこんな感じ.
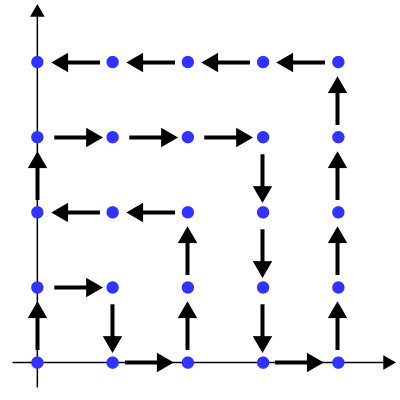
これも,x座標とy座標それぞれの奇偶,それとx座標とy座標のどちらが大きいか(直線y=xの下にあるか上にあるか,線上か)で場合分けすることで,任意の座標(x,y)から,次のステップへの向きが求められそうです.