例の解法(その1)

いきなりですが問題です．

を満たす整数，の組の一つを求めなさい．

今期の試験問題の一つです．実際には解くのに使うアルゴリズム名も明記していましたが，思うところあって，書かないことにします．Rubyで書いたコードは，http://d.hatena.ne.jp/takehikom/20080804/1217798940にあります．
手計算で求めるための，表をつくります．初期値は，こうです．

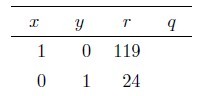
1行目は，，．2行目は，，．これは，の係数にかかわらず固定です．1行目のは，与えられた問題のの係数，2行目は，同じくの係数とします．変数は，初期化の際には使用しません．
アルゴリズムに従うと，行単位で次のと，，の順に求めていくのですが，先に，必要となるとのペアを求めておきます．

の値は，2行上のの値を被除数（割られる数），1行上のの値を除数（割る数）としたときの商で，その左隣すなわちの値は剰余（余り）となります．119を24で割ったら，商が4で余りが23．24を23で割ったら，商が1で余りが1．23を1で割ったら，商が23で余りが0．になったら，それ以上の値の更新はありませんので，表のおしまいを意味する横線を引いておきます．なお，「表の上部と底部，それと表頭の直後」の3箇所にだけ横線を引く作法は，フリーハンドで表を描くときだけでなく，論文でも利用可能です．
次に，との列を埋めていきます．3行目以降のそれらの値を求めるためのルールは，こうです．

値 = 2つ上の値 - 1つ上の値×同じ行のの値*1

3行目のは，で，1です．実は常に1です．

3行目のは，で，-4です．ここは，必ずになるとしてかまいません．

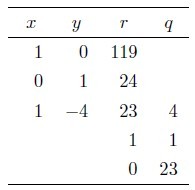
4行目のは，で，-1です．

4行目のは，で，1+4ですから，5です．

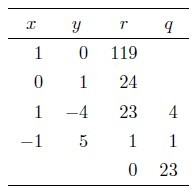
計算としては，これでおしまいです．の一つ上の行の，の値が，答えとなります．すなわち，，です．実際，は，なので1です．
上記のアルゴリズムは，演算回数（特に乗除算）が最小というわけではありません．しかし手計算で求める際に，計算ミスを容易に知ることが可能です．検算方法は，こうです．

（問題のの係数）×（の値）+ （問題のの係数）×（の値）=（の値）

この式が，表の各行について成立します．1行目，2行目でも成立します．実際には話が逆で，この等式が成立するように各行の値を定め，かつ計算によりの値が小さくなるように（アルゴリズムが有限ステップで終了するように）定めているのです．ついでに，の一つ上の行のの値は，問題のとの係数の最大公約数です．ここでは，119と24の最大公約数は1となり，最終的にという等式になったわけです．
次のチェックも，検算には有用です．

• 表の値はすべて整数であり，小数や分数は一切現れません．
• 3行目以降のとの値は，一方が正，一方が負です．具体的には，
  • 奇数行目のは正
  • 偶数行目のは負
  • 奇数行目のは負
  • 偶数行目のは正
• 下の行に行くほどは小さくなります．にはそのような順序関係はありません．

以上が，授業で説明し，試験の解答例で書いてきたことですが，との最後の行も埋めれば，もう一つ別の検算ができます．

計算方法は上述のものから変わりません．念のため式を書いておくと，のほうは，で24，のほうはで-119です．
最終行の，，の値で検算をすると，は，って筆算するまでもなく0です．このようにの値に，問題のの係数*2，の値に，問題のの係数が現れて，一方にマイナスの符号がつけば，計算は合っています．そうでなければ，どこかで計算ミスをしています．

*1:なので，との列を埋める際，は使用しません．しかし，，の3つ組が検算には有用なので，表は，，，の順に書くようにします．

*2:厳密には「問題のの係数」を「問題のとの最大公約数」で割った値となります．今回の計算ではその最大公約数が1なので，「問題のの係数」と一致しているというだけです．