わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

例の解法(その2)

授業

いきなりですが問題です．

9^{26} \bmod 29を計算しなさい．

例の解法(その1) - わさっきの続編です．今期の試験問題の一つで，こちらの出題の方が先でした．本日も，アルゴリズム名は書きません．
手計算で求めるための，表をつくります．初期値は，こうです．

使用する変数は，r，s，tの3つで，rの初期値は必ず1，sの初期値はべき乗の底，tは指数です．法となる29については，値は変わらないので表に現れません．
アルゴリズムに従うと，行単位でr，s，tの順に新しい値を書いていきますが，先にtの変化を求めておきます．というのも，rやsの変化に依存せずに計算でき，また，正当な方法で何回ループすれば計算が終了するかを，先に知ることができるからです．
具体的には，2で割っていき，端数は捨てて，0になるまで計算します．0になったら，表はそこまでなので，表の底部の横線も引きます．

tの初期値が十分に大きいとき，tの列の最後の3つは，「2，1，0」または「3，1，0」のどちらかになります．単純ミスを減らすのに有用です．
次はsです．これもまた，rやtの変化に依存せずに計算できます．2行目以降のsの値を求めるためのルールは，以下のとおりです．

値 = 1つ上の値{}^2 \bmod {}法

上に書いたとおり，この問題では法は29で固定です．具体的なsの値ですが，

  • 2行目は，9^2 \bmod 29 = 81 \bmod 29 = 23
  • 3行目は，23^2 \bmod 29 = 529 \bmod 29 = 7
  • 4行目は，7^2 \bmod 29 = 49 \bmod 29 = 20
  • 5行目は，20^2 \bmod 29 = 400 \bmod 29 = 23

6行目，すなわちt=0になるときのsの値は不要なので計算しません．表は次のようになります．

最後に，rの計算です．ただしこの列は，すべてのマスで計算するわけではありません．計算をしない行というのは，

1つ上のtが偶数のとき

です．先に，該当箇所に「↓」を書いておきましょう．

rの空きマスの値は，次のルールで，地道に，ミスすることなく計算する必要があります．

値 = 直前のrの値 × 1つ上のsの値 {}\bmod{}法

1の2行下の空白は，1×23で，これは29で割っても余りは変わりませんので，23を格納します．rの値を最初に更新するときは，「1つ上のsの値」と言ってもいいでしょう．

23の2行下の空白は，23\times20 \bmod 29 = 460 \bmod 29 = 25です．

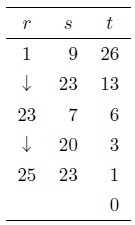
最後の行は，25\times23 \bmod 29 = 575 \bmod 29 = 24となります．

この24が，求めるべき，9^{26} \bmod 29の値となります*1．めでたしめでたし．
なのですが，計算ミスへの対策を，もう少し考えてみましょう．今回は先日のような，行単位で検算に便利な等式があるわけではなく，1箇所で間違えると，下の行がすべて間違いになってしまい，それに気づきにくいおそれがあります．
基本的な表チェックの方法は，次のとおりです．

  • tの列は，真に単調に減少します．最後の3つは「2，1，0」または「3，1，0」のどちらかです．
  • rの最後の行が「↓」になることはなく，そこでは必ず計算を行います．
  • rとsの列に出現する数値は，法（この問題では29）未満です．
  • rの列の値に関して，最初の行を取り除き，値が変更された箇所を1，値が変更されなかった箇所（「↓」と書いた箇所）を0に置き換え，最下段から上にあがる順にビット列をたどると，指数の2進数表現と一致します．この問題での1と0の置き換えは，最下段から上にあがる順に，変更あり(1)，変更あり(1)，変更なし(0)，変更あり(1)，変更なし(0)で，11010は10進数の26のことです．

最後の項目は，この計算の正当性を示す等式（関係式）から導くことができます．a^b\bmod nを計算する際，表の値は以下のようになります．

i行目のsの値 = a^{2^{i-1}}
i行目のrの値 = a^{b_i}\bmod n．ただしb_i=b\bmod 2^{i-1}

x^{y^z}は「（xのy乗）のz乗」ではなく（それは(x^y)^z = x^{yz}です），「xの（yのz乗）乗」です．すなわちべき乗演算は，C言語でいう右結合の演算である点に注意が必要です．
sの値は，最初は底a，そしてa^2，a^4，a^8，…をそれぞれ法nで割った値となります．そして，rはそこからa^b\bmod nを計算するのに必要な値だけを取り出して，掛け算し，nで割った余りを求めているということです．
といった，動作原理に基づくチェック方法では，不満のある人のために，よく使う裏技を一つ，書いておきましょう．剰余が絡む積についての，興味深い等式があります*2．証明は省略します．

(n-a)(n-b) \bmod n = ab \bmod n

法nに近い（したがって，少々大きな）2つの数を掛け算して，nで割った余りを求めるとき，2つの数をそれぞれ「nからその数を引いた値」に変更してよい，というルールです．
これを使うと，例えばsの列で，23の次が7になるところは，n=29，a=b=6を割り当てるとab=36となり，これを29で割ったら余りは7です．23^2 \bmod 29 = 529 \bmod 29 = 7として計算する方法に比べて，ずいぶんと簡単になります*3．
rの最後の値を求めるのは，(29-4)(29-6) \bmod 29 = 4\times6 \bmod 29 = 24です．
うまく使うと，乗算の手計算の手間を大きく減らせますが，その代わり，「nからその数を引いた値」のところで間違えやすいので，これに頼りすぎないようにしましょう．検算のツールとするのがいいと思います．

*1:翌朝追記：bcコマンドを起動して，「9^26%29」を入れると「24」と出ます．ついでに「9^26」だと，「6461081889226673298932241」というのが返ってきます．

*2:同日夜に式を変更しました．

*3:sの列で，9の直下と20の直下が，同じ値になることも，n=29，a=b=9により，確認できます．