縦に見る事例

• 例の解法(その1)

を満たす整数，の組の一つを求めなさい．

(略)
アルゴリズムに従うと，行単位で次のと，，の順に求めていくのですが，先に，必要となるとのペアを求めておきます．

• 例の解法(その2)

を計算しなさい．

(略)
アルゴリズムに従うと，行単位で，，の順に新しい値を書いていきますが，先にの変化を求めておきます．というのも，やの変化に依存せずに計算でき，また，正当な方法で何回ループすれば計算が終了するかを，先に知ることができるからです．
具体的には，2で割っていき，端数は捨てて，0になるまで計算します．0になったら，表はそこまでなので，表の底部の横線も引きます．

• アレイ図 (2015.12)

以下の図を対象として，この●の個数を表すかけ算の式を考えてみます．

●●●●
●●●●
●●●●

かけ算の式は，3×4とするのが一般的です．面白いことに，「かけられる数×かける数」を採用する日本でも，「multiplier × multiplicand」を採用する米国などでも，同じ式です．
日本ではこの図を次のように分けて，一つ分の大きさを3とし，それが4つあるので，3×4＝3＋3＋3＋3＝12と考えます．

●｜●｜●｜●
●｜●｜●｜●
●｜●｜●｜●

(略)
それはともかく米国では，もとの配置を横方向に切り分けて，以下の図のようにしてから，「3つの4 (three 4s, three times four)」と解釈し，3×4＝4＋4＋4＝12とします．

●●●●
――――
●●●●
――――
●●●●

• 表札は？ＡＫＡＭＯＴＯ

　まぎらわしい表札は，『OL進化論』で見たことがあります．二世帯住宅の表札です．1枚の表札に漢字が2×2で並んでいて，縦からも横からも読めるというものです．
　単行本を持っておらず，画像を検索しても，見つかりませんでした．こんな感じです．

中田
川村

　横に見ると，上から「中田」と「川村」，縦に見ると，右から「田村」と「中川」になるわけです．

• シーザー暗号の解読・2021年度版 - わさっきhb

　ずらす操作は，文字ごとに独立に行えます．例えばつぎのように書いて，2列目，3列目，…と書き出していくのでも，いいということです．

gzssd
h
i
j
(略)
d
e
f

• 算数教育に携わる人々は全国学力テストから何を見るか - かけ算の順序の昔話

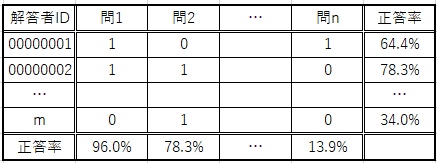
　ここで事例から離れます。「正答率」（「通過率」とも）について，架空の表を作ってみました。

(略)
　算数授業研究Vol.130の特集で，全国学力・学習状況調査の出題をもとに「つまずき」と書かれているのは，例外なく，問題ごとの正答率（表の最下段）を見たときに，低い値になっている出題と，結び付けられています。
(略)
　全国学力・学習状況調査の批判で見かける「学力」も，行ごとに算出される件と関連づけられるように思います。