かけ算・資料集2（2011年以降の書籍）

編集方針は，かけ算・資料集1をご覧ください．

目次

• 算数のつまずきには法則がある
• 小二教育技術 2012年11月号
• 親子で学ぶ数学図鑑
• 整数の計算
• 小数・分数の計算
• 学力チェックテスト算数2年生 改訂3版
• 2年生の文しょうだい
• 小学自由自在算数1・2年
• 算数好きにする教科書プラス坪田算数ワークブック2年生
• 小学教科書ドリル全教科書対応版文章題2年
• 小学校指導法 算数
• くもんの算数文しょうだい集中がくしゅう 小学2年生 改訂版
• 読み取り表す力を育てる「足場」のある算数授業
• 改訂版「まるわかり」小学校の算数
• 教育出版版 小学算数 2年
• まるごと2年生 2年生担任が まず読む本
• 小学できるできるドリル算数 2年
• 学ぼう!算数中学年用準拠版ワーク 上 改訂版
• いっきに極める算数 7
• ぐんぐんできる算数練習帳 2年
• だれでもできる基礎基本の授業 2年算数
• 通知表に役立つ観点別算数プリント集 小学2年生
• 小学校算数 これでバッチリ!計算指導
• かけ算には順序があるのか
• みるみるみにつく算数力 小学2年
• たす　ひく　かける　わる
• 田中博史の楽しくて力がつく算数授業55の知恵
• 算数科の宿題ファックス教材集 低学年
• 「板書見ながら」算数作文
• 算数授業研究 第77号
• 365日の算数学習指導案 1・2年編
• 小学２年　算数・国語のいつでも復習
• 小学校新卒教師に贈る算数科授業の基本技88
• ４マス関係表で解く文章題
• 小学校算数科授業の基礎技術Ｑ＆Ａ
• 先生のための学校　計算力が確実に伸びる指導
• 算数授業研究 第80号
• 田中博史の算数授業１・２・３年
• 小学校算数板書とノートを変えると子どもが伸びる
• 算数の教え方には法則がある
• 理系への数学2012年5月号
• 算数教科書の用語・記号教え方ガイドブック

整数の計算

整数の計算 (リーディングス 新しい算数研究)

〔問題〕８×６のもんだいをつくりました．よいものに○をつけなさい．
(1)（　）みかんが一つのおさらに８こ，もう一つのおさらに６このせてありますが，みかんはなんこありますか．
(2)（　）えんぴつを６本かいました．このえんぴつは１本８えんです．いくらはらえばよいですか．
(3)（　）１まい６えんのがようしを８まいかいました．いくらはらえばよいですか．
(p.117．《ＡＢ型》《ＢＡ型》)

3 同数列の長方形的配列(array)
例えば，右のような図では，縦に3個ずつ並んだ列が4列あるとみれば，○の数は3×4であり，横に4個ずつ並んだ列が3列あるとみれば，○の数は4×3と表せるから，交換法則は容易に理解できよう．
（図省略．図の下に「3×4＝4×3」）
(p.122．《複数解》)

小数・分数の計算

小数・分数の計算 (リーディングス 新しい算数研究)

T 今日の勉強は小数のかけ算です．

連休にお父さんやお母さんと遠くにドライブに行きました．満タンにするのに車にガソリンを入れたら，3.4Lでいっぱいになりました．ガソリンの値段は，1L120円です．ガソリン3.4Lでいくらになりますか．（会話を通して）

(略)
T どんな式で考えられますか．
C 120円×3.4
T ほかに違う式の人はいませんか．（声なし）
T この式でいいですか．
C ハイ．
(p.85)

また，実際に授業をして実感することは，子どもが式を軽視しているということである．算数の教科書が多くの場合「小数のかけ算」といったように，演算を示唆するような単元名になっており，「1mの値段が180円のリボンを3.4m買いました．代金はいくらでしょう」という問題であれば，子どもは単元名から，演算はかけ算であとは問題に出てくる順番に数字を並べていけばよいと考えている．そこには，演算の意味を考える必要はない．したがって，「リボンを3.4m買いました．1mの値段は180円です．……」という問題になると「3.4×180」と立式する子どもが出てくる．また，子どもにとって大切なことは，式そのものより答えが合っているかどうかということのようである．つまり，子どもにとって（ともすると教師にも）式は計算のためであり，心を配ることは「いかに正確に計算をして答えを出すか」なのである．
(p.105)

学力チェックテスト算数2年生 改訂3版

学力チェックテスト算数2年生 (くもんの小学ドリル)

ひろみさんは，がようしを 8まい かいます。がようしは 1まい 7円です。ぜんぶで なん円 はらえば よいでしょうか。
（p.92．この問題集の最後の問題．答えの式は「7×8＝56」(p.104)．直前の問題の解答は，式に「17＋8＝25（または，8＋17＝25）」と書かれている．）

2年生の文しょうだい（くもんの小学ドリル算数文章題2）

2年生の文しょうだい (くもんの小学ドリル 算数 文章題 2)

3つの はこに りんごが 5こずつ 入って います。りんごは ぜんぶで なんこ ありますか。

(p.64)

かけ算の しきを つくる ときは，かける数と かけられる数を ぎゃくに しないようにしよう。
(同)

かける数と，
かけられる数を
正しく しきに
かけたかな?
(p.94)

小学自由自在算数1・2年

自由自在算数小学1・2年

自どう車が 4台 あります。1台の 自どう車に 5人ずつ のります。みんなで 何人 のれますか。
(p.145．《ＢＡ型》)

この問題のように，「いくつ分」が先に示されている場合，示された数値の順に「4×5」とする子どもがいますが，これではかけ算の意味を理解しているとはいえません。「1つ分の数」と「いくつ分」を区別し，「5人ずつが4台分」であることから，式を書くようにします。
（指導マニュアルp.61）

算数好きにする教科書プラス坪田算数ワークブック2年生

算数好きにする教科書プラス坪田算数ワークブック2年生 (TEXT BOOK PLUS)

式に合うもんだいを作ります。( )にあてはまる数を書きましょう。

３×８

( )グループでゲームをします。1チームは( )人です。ぜんぶで何人いるでしょう
(p.59．《ＢＡ型》)

「３グループで１チーム８人」とまちがえやすいけれど、３×８の式があらわしているは、「３人の８グループぶん」だね
(p.149．上の解説)

□の数をあらわす式を選んで、( )にア〜エのきごうを書きましょう。
（図3つ省略）
ア　5×2　　イ　2×8　　ウ　3×4　　エ　4×3
(p.58．《複数解》)

小学教科書ドリル 全教科書対応版 文章題 2年

小学教科書ドリル 全教科書対応版 文章題 2年

② □×□の 答えと 7＋7＋7＋7の 答えは 同じに なります。答えは □です。
(p.30)

ふくろが 7こ あります。1つの ふくろに 3こずつ くりを 入れます。くりは 何こ いりますか。
(p.34)

ご石の 数を くふうして もとめましょう。

(p.41)

小学校指導法 算数

小学校指導法 算数 (教科指導法シリーズ)

2. 「子どもが7人います。1人に4個ずつアメをくばります。アメはみんなで何こいりますか」という問題に対して、7×4＝28答え28こ、と解答した小学校2年生の子がいました。この解答をどのように解釈して、どのような対応をしたらよいか、乗法の意味と関連させてまとめてみましょう。
(p.96．《ＢＡ型》)

乗法の場面、「1ふくろにミカンが3こずつ入っています。5ふくろでは、ミカンは何こでしょう。」は、3×5と立式される。立式は、「1つ分の数×いくつ分＝全体の数」とまとめられ、それぞれ被乗数、乗数という。ところで、「オリンピックの400メートルリレー」や「このDVDは16倍速で記録できる」、「xのk倍は」の式は、どのように表わされるであろうか。それぞれ、一般的には「4×100mリレー」、「16×」*1、「kx」と表される。被乗数と乗数の位置が教科書の書き方と逆になっていることに気付くであろう。この例から分かるように、乗法では、数の位置ではなく、数が意味する内容に注目して、どの数が1つ分の数であるか、いくつ分はどの数かをしっかりと読み取ることが大切である。第2学年や第3学年では、読み取った数を、「1つ分の数×いくつ分＝全体の数」と表現できることが重要であり、逆に、この立式ができているかで、数の読み取りができているかを判断できる。しかし、高学年になり、乗法では交換法則が成り立つことや外国での立式を知り、数の意味をしっかり理解できていれば、必ずしも第2学年で学んだ順序で立式することを強制しなくてもよい。
(pp.91-92)

くもんの算数文しょうだい集中がくしゅう 小学2年生 改訂版

くもんの算数文しょうだい集中がくしゅう 小学2年生

おなじ あつさの ノートを 8さつ つみました。ノート 1さつの あつさは 6mmです。ぜんたいの あつさは なんcmなんmmに なりますか。
(p.133．《ＢＡ型》)

読み取り表す力を育てる「足場」のある算数授業

読み取り表す力を育てる「足場」のある算数授業―すぐに使える!読解問題付き

ベンチが4つあります。1つのベンチに子どもが3人ずつ座りました。まだ，5人立っています．子どもは全部で何人いるでしょう。

T この問題を図でかいてみましょう。
T 図Aと図Bのどちらが，この問題に合っていますか。
C 図Bは，4人ずつになっているから違う。
C 図Aは，3人ずつだし，ベンチも4つある。
T 図を見て，どんな式になるのか説明しましょう。
C 3人ずつのまとまりが4つあるので，3×4です。まだ，5人残っているので，それをたします。
○問題文では基準量が後に示されているので，図をかくことによって，3が基準量であり，4がいくつ分であることを理解させる。

(p.29)

エントリ：2×30g

改訂版「まるわかり!」小学校の算数

改訂版「まるわかり!」小学校の算数 (わかる!できる!のびる!ドラゼミ・ドラネットブックス―日本一の教え方名人ナマ授業シリーズ)

もうひとつ大切なことは、かけ算の式は、
1あたりの数×いくつ分＝ぜん体の数
というようにしなきゃいけないことだ。たとえば「1人に3こずつ、4人にくばるときのぜんぶの数は?」というとき、
3（こ）×4（人）＝12（こ）
とするんだ。3×4も4×3も答えは同じだけど、式をたてるときはかならずこのじゅん番でたてようね! 4(人)×3(こ)＝12(人)は、まちがいだよ。
(p.45)

（ジャイアン）いいこと聞いたぞ。オレは7のだんが苦手だから、7×6が思い出せないときは、6×7の九九を思い出せばいいんだな。
（ドラえもん）そういうこと。でも、文章題で式をたてるときは、ちゃんと「1あたりの数×いくつ分＝全体の数」としなきゃ、まちがいだよ。
(p.52．「（ジャイアン）」と「（ドラえもん）」は原文ではそれぞれ顔の絵)

教育出版版 小学算数 2年

教育出版版 小学算数 2年 (教科書わかるわかるテスト)

つぎのもんだいをかけ算でもとめましょう。
(1) ベンチが8つあります。1つに2人ずつすわると，何人すわれますか。
(2) おかしぶくろが8つあります。1つのふくろにはチョコレートが5こずつはいっています。チョコレートはぜんぶで何こありますか。
(p.65．《ＢＡ型》)

(1)(式)2×8＝16 (答え)16人
(2)(式)5×8＝40 (答え)40こ
（てびき）問題文に出てきた順で式をつくると，×の前後が逆になってしまいます。求めるものがかけられる数の単位になることを確かめさせましょう。
(答えとてびき p.13)

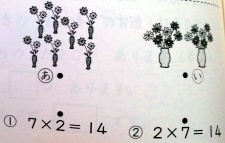
3×7の式になるもんだいを□からえらんで，きごうで答えましょう。
(あ) ボートが7そうあります。1そうに3人ずつのると，ぜんぶで何人のれますか。
(い) いすが3つあります。1つに7人ずつすわると，ぜんぶで何人すわれますか。
(う) りんごが1かごに7こずつ入っています。3かごぶんでは何こになりますか。
（右に吹き出し）かける数とかけられる数がいくつか考えてね。
(p.69．《ＡＢ型》《ＢＡ型》)

（てびき）(い)(う)は，7×3の問題で，かけられる数とかける数が逆です。●×▲の●や▲の選び方は，間違えやすい点です。区別する方法には，
・求めたいものを，かけられる数にする
・答えと同じ単位のほうが，かけられる数
などがあります。
(答えとてびき p.13)

まるごと2年生 2年生担任が まず読む本

まるごと2年生 2年生担任が まず読む本 (教育技術MOOK)

(p.16)

小学できるできるドリル算数 2年

小学できるできるドリル 算数2年

長いすが 4つ あります。1つに 7人ずつ すわると，ぜんぶで 何人 すわれますか
(p.37．《ＢＡ型》)

答えが 24に なる 九九を ぜんぶ 書きましょう
(p.40．《複数解》)

学ぼう!算数中学年用準拠版ワーク 上 改訂版

学ぼう!算数中学年用準拠版ワーク 上 改訂版

けんじさんのクラスは，全員で34人います。1人に15まいずつ半紙を配るとすると，全部で何まいいりますか。
(p.11．《ＢＡ型》)

いっきに極める算数 7

いっきに極める算数 7 小学3~6年の文章題

クラスの人数は27人です。工作用紙を1人に4枚ずつ配ります。工作用紙は何枚用意すればよいですか。
(式)
1人分の枚数　人数　全部の枚数
□×□＝□
(p.13．《ＢＡ型》)

大中小の3種類の箱があります。小の箱にはケーキが2個入ります。中の箱には小の箱の2倍のケーキが入り、大の箱には中の箱の4倍のケーキが入ります。大の箱には、何個のケーキが入りますか。
(式)
小の箱に入る数　中が小の何倍　大が中の何倍　大に入る数
□×□×□＝□
(p.15．「3」は式に使用しない)

ぐんぐんできる算数練習帳 2年

ぐんぐんできる算数練習帳 小学2年 おもしろい問題がいっぱい

(3) ずこうしつには つくえが 8つ あります。どのつくえにも いすが 4こずつ あります。ぜんぶで 何こですか。
(p.95．《ＢＡ型》)

（しき）4×2

(1) しきに あう 絵は どちらですか。（　）に ○を しましょう。
（図省略）
(p.96)

絵に　あう　かけ算の　しきを　線で　むすびましょう。

(p.104)

だれでもできる基礎基本の授業 2年算数

だれでもできる基礎基本の授業 2年算数

1. チョコレートが 1はこに 8こずつ 入っています。5はこ あります。 チョコレートは ぜんぶで 何こ ありますか。
　　1あたりの数　×　いくつ分
　　（　　　）こ　　（　　　）はこ
2. 4まいの ふくろに バナナを 3本ずつ 入れます。バナナは ぜんぶで 何本 いるでしょう。
　　1あたりの数　×　いくつ分
　　（　　　）こ　　（　　　）ふくろ
(p.33．《ＡＢ型》《ＢＡ型》)

2.を黒板に書き全員で読みます。ここでもバナナが3本ずつ入ったビニール袋を4枚用意します。
T: 1あたりの数はどれでしょう。
S: 3本です。
T: バナナはビニール袋に入っています。何袋ありますか。
S: 4袋です。
プリントに式を書かせます。ここでは前時の皿から箱、袋になっても「1あたりの数×いくつ分」で全部の数が求められることを理解させます。
(p.32)

【1あたりの数が先に出てくる問題】
1. 1はこに6こずつケーキを入れていきます。7はこでは、何こになりますか。
（しき）6×7＝42　答え 42こ
【1あたりの数があとに出てくる問題】
1. 長いすが6つあります。1つのいすに4人ずつすわります。みんなで何人すわれますか。
（しき）4×6＝24　答え 24人
(p.103．《ＡＢ型》《ＢＡ型》)

「1あたりの数（量）×いくつ分」を前後反対にして立式する子がいます。かけ算の意味を理解させるためにも式に助数詞をつけさせるといいでしょう。
(p.102)

通知表に役立つ観点別算数プリント集 小学2年生

通知表に役立つ観点別算数プリント集 小学2年―コピーしてすぐに使える

5人ずつ のって いる じょう用車が 6台 あります。じょう用車に のって いる 人は、みんなで 何人ですか。
(p.98．《ＡＢ型》．「しき」として「5×6＝」が薄く書かれており，なぞればよいようになっている．)

長いすが 7つ あります。1つに 8人ずつ すわると、ぜんぶで 何人 すわれますか。
(p.115．《ＢＡ型》)

●の 数を もとめる かけ算の しきを 2つ かきましょう。
（図は省略．回答欄は「しき」と式を書く欄が2つある．）
(p.123．《複数解》)

小学校算数 これでバッチリ!計算指導

小学校算数 これでバッチリ!計算指導 (指導のこつシリーズ)

1mの重さが3kgの鉄のぼうがあります。この鉄のぼう12mの重さは何kgでしょう。
(p.127．《ＡＢ型》．式の正答率が，答えの正答率よりもかなり低い)

6つのはこに、ケーキが8こずつはいっています。ケーキはぜんぶでなんこあるでしょう。
（正解）8×6
(p.72．《ＢＡ型》．2年生を対象として，立式の正答率は50.8%)

多い誤答
かける数とかけられる数を逆に立式してしまう。
問題文に出てきた数の順に立式してしまった子どもが、34.7%みられました
(p.72)

かけ算には順序があるのか

かけ算には順序があるのか (岩波科学ライブラリー)

いま，小学校では，「6人に4個ずつミカンを配ると，ミカンは何個必要ですか」という問題に，6×4＝24という式を書くと，答えはマルで，式はバツにされます．
(p.iii．《ＢＡ型》)

みるみるみにつく算数力 小学2年

みるみるみにつく算数力小学2年

5人の 子どもに，1人に 2こずつ あめを くばります。
あめは 何こ いりますか。
(p.43．《ＢＡ型》)

〔しき〕2×5＝10　　　答え 10こ
ときかた　1人に 2こずつ 5人分です。
（答えとときかた p.16）

たす　ひく　かける　わる

算数の探険1　たす　ひく　かける　わる（加減乗除）

本シリーズ「算数の探検」は，ほるぷ出版より1973年に刊行された『算数の探検』（全10巻）を復刊したものです。
（奥付）

問題　おいしいチョコレートが入った箱が3つある。重さをはかったら，どれも327グラム。さて3つで何グラムか?
(p.60)

12人の小人が上の絵のように，手をつなぐと3×4，下のように手をつなぐと4×3になる。4×3も3×4も同じ12が出るね。

(p.135)

エントリ：HTHT

田中博史の楽しくて力がつく算数授業55の知恵

田中博史の楽しくて力がつく算数授業55の知恵―おいしい算数授業レシピ〈2〉 (hito*yume book)

（表）5×8
（裏）
1はこに5こ入りの
チョコレートが
8はこあります。

（表）8×5
（裏）
チョコレートが
5はこあります。
1はこは8こ入りです。

（九九カルタ　文溪堂より）
(p.48．《ＡＢ型》《ＢＡ型》)

算数科の宿題ファックス教材集 低学年

新教育課程対応算数科の宿題ファックス教材集 低学年

長いすが3つあります。1つの長いすに4人ずつすわると何人すわれますか。
(p.86．《ＢＡ型》)

「板書見ながら」算数作文

「板書見ながら」算数作文―話すだけの授業からの脱却

今日の算数の時間に，21×3の計算の仕方を考えました。それで最初に，21×3でとける問題をつくってみました。ぼくはつくってもう1回読んだら，3×21になってしまっていたので，すぐ書き直しました。
次に，21×3の仕方を考えました。(以下略)
(p.6)

エントリ：HTHT

算数授業研究 第77号

算数授業研究 77 特集:まるごと1冊新内容の算数授業!ここがポイント

池の周りを4周走りました。
1周312mです。
全部で何m走ったでしょう。
(p.66．《ＢＡ型》)

365日の算数学習指導案 1・2年編

活用力・思考力・表現力を育てる!365日の算数学習指導案 1・2年編

第2次 第10時 基準量が後に示された適用問題
１　問題を知り，めあてをつかむ。

おかしのはこが4つあります。
1つのはこには，おかしが5こずつはいっています。
みんなで何こになりますか。

5×4か4×5のどちらになるか考えよう。

５　学習のまとめをする。

「何のいくつ分」に気をつけてもんだいをとくとよい。
5この4つ分。
5×4＝20　20こ

(p.104．《ＢＡ型》)

第1時　具体物をまとめて数える

子どもが3人います。みかんを1人に2こずつあげます。みんなでなんこいりますか。

○1個ずつ置くか，2個ずつ置くかという置き方ではなく，置いた結果に着目させる。

(p.66．かけ算ではなく，「同数累加」「数の乗法的な構成」に関する授業例．)

小学２年　算数・国語のいつでも復習

小学２年　算数・国語のいつでも復習

ボートが 5そう あります。1そうに 2人ずつ のると，ぜんぶで 何人 のれますか。
(p.31．《ＢＡ型》．問題番号の左横に白抜きで「ちゅうい」，答えを書く欄の左に青色で「かけ算の しきの いみを よく 考えて，しきを 書こう。」とある)

問題文に出てくる数の順に，5×2＝10と立式しないように注意させましょう。「1つ分の数」にあたる数，「いくつ分」にあたる数を，それぞれ問題文から読み取り，（1つ分の数）×（いくつ分）と立式するように指導してください。
(算数 べっさつ 答えとアドバイス p.6)

広場に はとが 何わか いました。
7わ とんで いったので，のこりは 15わに なりました。
はとは，はじめに 何わ いましたか。
(p.42．解答（算数 べっさつ 答えとアドバイス p.8）には，正解として「7＋15＝22　22わ」を挙げており，同じページに「式は，15＋7＝22でも正解です。」とある)

小学校新卒教師に贈る算数科授業の基本技88

小学校新卒教師に贈る算数科授業の基本技88

次の①問題は，ほとんどの子どもが正解します。ところが，②の問題では逆に多くの子どもが間違います。

問題①　1はこに6こずつ入ったせっけんが4はこあります。せっけんはぜんぶで何こありますか。	問題②　せっけんの入ったはこが6はこあります。1はこに4こずつ入っています。ぜんぶで何こありますか。
正答　6×4＝24　答え24こ	誤答　6×4＝24　答え24こ

②の誤答には，「かけ算の意味が理解できていないため，数値の出てきた順にかけた。」「①のような文章題の経験しかなく，数値の出てきた順にかけた。」の2つの原因が考えられます。
問題の様子を図に表してみる，数量の関係をかけられる数（基にする数，1つ分）やかける数（いくつ分，何ばい）で捉えてみることなどかけ算の意味の理解を深める学習をさせます。また問題①と②を比べさせ，図で表した場面と式を対応させて違いを理解させることも有効です。問題の理解，立式，計算，答えを総合的に練習させる必要があります。
（p.40．「基本技16 乗法九九は練習と活用の繰り返し」）

4マス関係表で解く文章題

筑波大学附属小学校田中先生の算数4マス関係表で解く文章題―小学4・5年生 (有名小学校メソッド)

例題1 重さ0.4kgの本が6さつあります。重さは全部で何kgになりますか。
(略)
(式) 0.4×6＝2.4　答え2.4kg
この式は，ことばの式で書くと，ふつう 1さつの重さ×さっ数＝全部の重さ と表します。
でも，この式の意味をもっと正確に書くと，0.4(kg)×6(さつ)ではなく，0.4kgの6倍という意味だということを理解しておきましょう。
(p.12)

小学校算数科授業の基礎技術Ｑ＆Ａ

プロ教師に学ぶ 小学校算数科授業の基礎技術Q&A

■教師の「簡単」と子どもの「簡単」は違う
授業で、ある問題の解き方がいくつか出されました。そこで教師は「一番簡単なのは、どれですか」という問いかけをしました。教師は「効率的」というような意味で「簡単」という言葉を使い、かけ算を用いた解法に目を向けさせるのが意図でした。しかしある子どもが、「僕は、たし算を繰り返して足していくほうが簡単だ」と言って譲りません。この子どもは「簡単」という言葉を「自分にとっての計算のしやすさ」といった意味でとらえていました。「簡単」という言葉は、算数では「効率的」という意味合いが強くなりますが、子どもはそのようにとらえるわけではないので、教師が困惑したり、納得させようと説明したりしてしまうことがあります。このような状況を避けるために、「式の数が少なかったり、計算する回数が少なかったりする式を『簡単な式』と考えます。皆さんが考えた中で『簡単な式』はどれですか」と問いかけることも有効です。同じ言葉でも、教師と子どものとらえ方が違う場合があることに留意して、発問することが大切です。
(p.93)

(p.94)

■式は事柄を表す
黙って、黒板に上のように書きます。そして「何でしょう」と問いかけます。子どもたちは、自信満々で手を上げ「十二です」と答えます。少し間をとった後「違います!」ときっぱり言うと、どの学級でも「えーー」という声が響きます。しばらくすると、「かけ算」「二十六」「二と六」などと答えます。
一通り子どもたちの考えを聞いた後、「式は答えを出すだけのものではありません。この教室の中にあるものを表しています。何を表しているのかわかったら、先生のところに来て、小さな声で教えてください」と説明・指示をします。
(p.95)

先生のための学校　計算力が確実に伸びる指導

先生のための学校 計算力が確実に伸びる指導 (教育技術MOOK 先生のための学校)

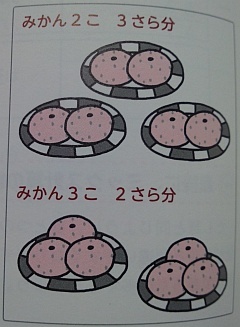
助数詞をつけると理解しやすい

式　2こ×3さら分＝6こ
式　3こ×2さら分＝6こ

これらの答えは6個と同じですが、式にすると全く逆です。
具体的なイメージをつかみにくい場合でも、助数詞（単位）をつける立式の間違いはほとんどなくなります。
このことによって、もとにする量×いくつ分がかけ算だということを理解させることができます。
また、三年生のわり算の学習で、等分除と包含除の違いがわかりやすくなりますし、小数や分数の文章題を習うときにも、この助数詞があることによって、立式の間違いを防ぐことができます。
(pp.22-23)

算数授業研究 第80号

算数授業研究 VOL.80

（p.11．磯田正美「我々は，何を，なぜ，いかに教えるか」）

「1mが120円のりごん2.7mのねだんはいくらか」(略)
このかけ算を2.7×120と書く子どもがいたらどうしようか。「なぜ，そう書いたのか」と聞くことになるだろう。その子が「もし1mのねだんが1円なら，2.7mのねだんは2.7円でしょう。でも，1mが120円だから，その120倍になる」と答えたら，これは素晴らしい。幸か不幸かまだ，そういう子どもに出会ったことはない。大切なことは，その式を支えているイメージを伴っているかどうかである。
（p.53．正木孝昌「かけ算のイメージを育てたい」）

田中博史の算数授業１・２・３年

田中博史の算数授業1・2・3年 (算数授業研究特別号)

本当にかけ算の表現がわかるかどうかを試すため，次のようないじわるな文章も入っている。

2こで1パックのプリンと，5こで1パックのプリンを1パックずつかいました。

「1パック」「ずつ」というような表現があると，かけ算だとすぐに考えてしまう子どももいて，これで2×5とする子がいる。
でもこの文章を絵にすると，次のようになる。
（図省略）
そうである。
単純なたし算の問題なのである。
(p.38)

先ほどの文章題カルタとは，目的を別にした九九専用のカルタも作ってみた。
こちらは『ビジュアル九九カルタ』（文溪堂）という。
かけ算の文章表現と式表現の約束を理解させることと，九九を覚えること，九九表の中の数のきまりを発見することなど九九全体の学習を目的としているので，こちらのほうはすべての九九をカードにすることが必要になる。カードは読み札が下のようになっており，絵札が別に付いている。

(p.38)

小学校算数 板書とノートを変えると子どもが伸びる

小学校算数 板書とノートを変えると子どもが伸びる

(p.31)

教科書問題場面は絵で示されている。
そこで，問題場面の1つぶんの数といくつ分とを把握しやすくするために，人をブロック（半具体物）で表し，以下の手順で板書する。

1. 問題分を板書し，さし絵を黒板に貼る。（さし絵は，人の絵をブロックに置き換えた後はがす。）
2. のりものが3台あることを確認し，3台分の枠を板書する。
3. 1台目ののりものに乗っている人を，板書上で児童と一緒に，一人ずつブロックに置き換え，6人乗っていることをおさえる。
4. 2台目，3台目も，3と同様にして，6人乗っていることをおさえる。
5. どののりものにも6人ずつ乗っていることを，のりものごとにブロックを数えてその上に6と板書し，「1台に6人ずつ，3台分あり，18人いること」をおさえる。
6. ブロック図で確認した「1台に6人ずつ3台文で18人」を児童に唱えさせ，ブロック図の下に板書する。

(p.32．箇条書きの番号は原文では丸囲み数字．2〜5の説明文の直後の図は省略した．)

3年 計算のしかたを考えよう(11/13時)
・本時は「かけ算はかける順番を入れ替えても答えは同じ」であることを学ぶ時間なので，問い方を工夫して一つの式にすることは正しいかを考えさせていく。

問題　1こ60円のおかしが1はこに4つ入っています。このはこを2つ買うと，代金はいくらですか。

まとめ　3つのかずのかけ算では，はじめの2つの数を先に計算しても，あとの2つの数を先に計算しても答えは同じになる。
（60×4）×2＝60×（4×2）

・4×2×60は問題場面に合わないので取り上げず，イのように8は4×2である確認から，60×（4×2）にもっていくようにする。
(p.50．ページ内の主要部のみ)

算数の教え方には法則がある

算数の教え方には法則がある

(2) 子どもが作る文章問題のほとんどは，出てくる数字の順序で計算する
(略)
だから，次のようなかけ算問題には混乱が生まれる。
「ベンチが5こあります。そこに6人ずつすわっています。ベンチにすわっている人は何人でしょう」
問題をつくったA男は，数字の順序で5×6としてしまった。
そこで「絵」を描かせると，「ああそうか」とA男は6×5の式が立てられた。
（図省略）
(p.71)

親子で学ぶ数学図鑑

親子で学ぶ数学図鑑:基礎からわかるビジュアルガイド

(p.19)

(p.29)

関連：数学図鑑

理系への数学2012年5月号

理系への数学 2012年 05月号 [雑誌]

(p.88．京都大学創作サークル「名称未定」（作画:フーフー&あむせ）：「ますまて」)

上は4コマ漫画の2番目のコマで，2012年4月26日にも記した．

算数教科書の用語・記号教え方ガイドブック

若手教師必携! 算数教科書の用語・記号教え方ガイドブック

×は，乗法（かけ算）の操作を表す計算記号である。×は1631年にイギリスのオートレッドの本の中で使われた。彼の本には「乗法を美しくするために2つの数をinまたは×で結ぶ」と書いてあるそうだ。
乗法（かけ算）は，元来は3＋3＋3＋3のように同じ数を次々とたしていくことを簡単にすることから始まった。これを同数累加という。現在ではもう一歩前進して，1つ分の大きさが決まっているときに，そのいくつ分かに当たる大きさを求める場合に用いられるのがかけ算である。基準量のいくつ分ともいう。
3＋4と3×4では，同じ数字ではあるが意味が異なる。3＋4の場合だと3こ＋4こ，3cm＋4cmなのに対して，3×4の場合は，4こ×4つ分，3cm×4つ分とおなる。
(p.24)

小二教育技術 2012年11月号

小二教育技術 2012年 11月号 [雑誌]

子どもの実態②
「一つ分の数×いくつ分の数」で表すかけ算の式の意味を十分に理解していないと、「かけられる数」と「かける数」が逆転してしまいます。
↓
指導の手立て
たし算の式からかけ算の式を考える練習をしましょう。
(p.55; )

子どもの実態⑥
かけ算の文章題で立式をする際に、数値を問題文に出てくる順に式をつくっています。「一つ分の数」と「いくつ分」の数値が逆転してしまいます。
【もんだい】
３まいの　おさらに　４こずつ　りんごを　おきました。りんごは、ぜんぶで　何こでしょう。しきも　書きましょう。
しき　3×4＝12　答え12こ
↓
指導の手立て
「一つ分の数」が後から出てくる文章題で、練習をしましょう。
(p.59; )

関連：新発見がなくても

算数のつまずきには法則がある

算数のつまずきには法則がある クラス全員クリアできる,驚異のスモールステップ指導法

「かけ算」という言葉を学習した後，絵を見て，かけ算の式をつくるという学習場面である。
（東京書籍2下p.7／啓林館2下p.20／学校図書2下p.10／教育出版2下p.6／大日本図書2下p.20／日本文教出版2下p.8）

上記のような絵をかけ算の式にするところで，つまずく子がいる。
2×5と式を書けなければならないのだが，5×2などとしてしまうのだ。
これは，「1つ分」「いくつ分」などの言葉が定着していないことが原因である。
(p.50)

2個ずつが5皿分。
かけ算の式を教科書に書き込みなさい。

作業させた後に，教師が大事なことをもう一度繰り返す。これによって，子どもたちは式が書きやすくなる。この繰り返しをしていくしかない。
(p.51)

関連：新発見がなくても

*1:引用者注：p.91右下に図5-14として，このように表記されている写真が載っている．