かけ算の順序論争について(日本語版)
「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」という出題と,「しき」と「こたえ」を書く欄からなる.(略)問題文では5が先,3が後に出現しているが,学習した「かけ算の意味」をもとに,2つの数をひっくり返して「3×5」と書かないといけない,というのが「かけ算の順序」の基本的な考え方である.
上記と同じ意図の出題事例で,2013年までのものを紹介していきます.
2013年:台湾の報道
- http://www.chinatimes.com/realtimenews/20131116002929-260413(デッドリンク)
2013年11月16日の報道です.問題文は「一打鉛筆有12枝,毎枝賣8元,一共幾元要如何計算?①8×12②12×8③8+12④12+8。」で,日本語に訳すと「鉛筆1ダースは12本である.鉛筆が1本8元のとき,全部で何元になるかを,どの式で求めればよいか(選択肢は省略)」です.
動画の途中では,老師(先生)がホワイトボードを使って解説しており,「被乘數」「單位」をかけ算の記号の左に,「乘數」「數量」を右に書いています.
2013年:授業に役立つ算数教科書の数学的背景
第2に,既習内容や発展内容に高い見通しをもつことで,子どもの問題解決上の気づきをより的確に評価できることです。例えば,「3人の友だちにみかんを4こずつあげます。みかんは全部でいくついりますか」という問題に対して,田中さんは3×4=12,鈴木さんは4×3=12と立式して答えを求めたとします。これを“みかん4こが3人分必要”だから,田中さんは誤っていると評価することも,3×4=4×3だからどちらも正しいと演算の交換法則を式解釈に持ち込んで評価することも早計といえます。
(p.9.執筆者は小原豊)
2013年:算数の学習プリント
[もんだい1] つぎのもんだいがあります。
4つのプランターに3つずつチューリップのきゅうこんをうえます。きゅうこんはなんこいりますか。
①たし算の式で答えをもとめましょう。
式 答え
②かけ算の式で答えをもとめましょう。
式 答え
(p.33)
関連:2. 算数の学習プリント
2013年:算数科問題解決授業スタンダード
本時の問題「3まいのおさらにりんごが6こずつのっています。りんごはぜんぶで何こですか。」を板書すると,子どもたちは「かけ算だ!」とすぐに解決しようとする。
そこで,自力解決の時間をとり,一斉に答えだけを問うと,「18」と全員の声がそろう。「それでは,式も一緒になりそうだね」と言いながら式も一斉に言わせると「3×6」と「6×3」の2つの式が出てきてしまうのである。
(p.52)
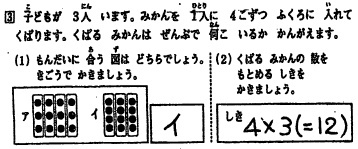
2013年:東京都算数教育研究会 学力実態調査
[3] 子どもが 3人 います。みかんを 1人に 4こずつ ふくろに 入れて くばります。くばる みかんは ぜんぶで 何こ いるか かんがえます。
2011年:365日の算数学習指導案 1・2年編
「子どもが3人います。みかんを1人に2こずつあげます。みんなでなんこいりますか」
(p.66)
「具体物をまとめて数える」と題した,第1学年向けの授業例です*1.「1個ずつ置くか,2個ずつ置くかという置き方ではなく,置いた結果に着目させる」を,指導上の留意点として挙げています.
関連:りんごのかけ算
2011年:かけ算には順序があるのか
いま,小学校では,「6人に4個ずつミカンを配ると,ミカンは何個必要ですか」という問題に,6×4=24という式を書くと,答えはマルで,式はバツにされます.
(p.iii)
2011年:東京書籍 平成23年度版 小学校教科書 新しい算数
ボートが 3そう あります。
1そうに 2人ずつ のって います。
ぜんぶで 何人 のって いますか。
つぎの 2つの もんだいの,しきと 答えを 考えましょう。
(1) えんぴつを 1人に 2本ずつ,5人に くばります。
えんぴつは,ぜんぶで 何本 いりますか。(2) えんぴつを 2人に 5本ずつ くばります。
えんぴつは,ぜんぶで 何本 いりますか。
2011年:大日本図書 教科書 平成23年度版 たのしい算数 2年下
- http://www.dainippon-tosho.co.jp/sho/sansuu/text/index.html(デッドリンク)
- http://www.dainippon-tosho.co.jp/h23/sansu/sansulink/sa11/default1.html(デッドリンク)
つぎの 2人の つくった もんだいは,2×6と 6×2の どちらの しきで もとめれば いいでしょう。
2つの ふでばこに えんぴつが 6本ずつ 入って います。
えんぴつは 何本 あるでしょう。
(つばさ)えんぴつを 1人に 2本ずつ,6人に くばります。
えんぴつは 何本 いるでしょう。
(あおい)
2011年:小学校指導法 算数
2. 「子どもが7人います。1人に4個ずつアメをくばります。アメはみんなで何こいりますか」という問題に対して、7×4=28答え28こ、と解答した小学校2年生の子がいました。この解答をどのように解釈して、どのような対応をしたらよいか、乗法の意味と関連させてまとめてみましょう。
(p.96)
関連:小学校指導法 算数
2010年:「子どものために」は正しいのか
算数の基礎基本とは何か
ここ数年は、基礎基本の徹底が声高に叫ばれ、九九の暗記に力を入れている学校や家庭が増えています。でも私の目には、単なる計算のトレーニングになってしまっているように見えるのです。どういうことかというと、「8×4は?」と聞くと「32!」と即答できるけれども、「8×4」と「4×8」の違いがわからない。この違い、あなたは説明できますか?
ではここで問題を出してみましょう。「ガラス戸が8枚あります。1枚のガラス戸につき、4枚のガラスが入っています。ガラスは全部で何枚あるでしょうか。式を立てて、答えをもとめなさい」。今の子どもは、32という答えはすぐ出せます。しかし、式を「8×4」と間違える子どもがとても多いのです。
かけ算とは、(1あたり量)×(いくつ分)=(全体の量)です。よって、この問題なら、式は「4×8」が正解。今の教育は、九九の暗記には力を入れているけれども、こういう本当の基礎基本を省く傾向にあります。かけ算が(1あたり量)×(いくつ分)=(全体の量)である、という基礎基本をしっかり理解していれば、その後の学びも楽になります。子どもがつまずきやすい割り算や小数、最大の難関である分数だって、へっちゃらなのです。「割り算とは、1あたり量を求めるのか、いくつ分を求めるのかの二通りしかない」と気づけます。しかし、この基礎基本を理解せずに九九の計算能力だけを鍛えて通過してしまうと、割り算や小数、割合、分数などが登場したときにつまずきます。つまずくと、今度は公式や計算方法を暗記させて乗り越えさせようとする。そのときはわかった気になるかもしれませんが、また別の問題が出たときにつまずくという悪循環になってしまいます。
本当の基礎基本とは何かを見抜き、しっかり身につけることが大事なのです。
(pp.123-125)
関連:https://twitter.com/flute23432/status/1237035441078992896
2009年:田中博史の算数授業のつくり方
「船が5そうあります。1そうに4人ずつ乗ることにします。」このような問題文になっていると子どもは必ず式を間違えますよね。「5×4」と書きます。今まで文の中に出てきた順番に数を使って式を書くだけで,ずっと丸をもらえていた子たちは,必ずこういう問題で引っかかります。
(p.62)
2008年:小学校学習指導要領解説 算数編
さらに,除法の逆としての乗法の問題,例えば「ひもを4等分した一つ分を測ったら9cmあった。はじめのひもの長さは何cmか。」のような場合にも,乗法が用いられることを理解できるようにする。
(p.107)
第3学年の出題です.
2008年:小学2年生の乗法場面に関する理解
- 金田茂裕: 小学2年生の乗法場面に関する理解, 東洋大学文学部紀要 教育学科編, No.34, pp.39-47 (2008). http://ci.nii.ac.jp/naid/40016569351
作問a 5×6になる算数のお話をつくりましょう
作問b 絵をみてかけ算になるお話をつくりましょう
文章題a 1はこに 4こずつ ケーキを 入れていきます 6はこでは なんこに なりますか
文章題b おかしの はこが 3つあります 1つの はこには、おかしが 5こずつ はいっています みんなで なんこに なりますか
(p.41)
第2は、被乗数と乗数に対する理解の程度に関することである。小学2年生では、文章題bにおいて被乗数と乗数が逆になった解答が多くみられた。この結果から、被乗数と乗数の区別に関する理解は、交換法則を学習していない小学2年の時点で不十分である可能性が示唆される。一方、大学生についても、文章題bにおいて被乗数と乗数が逆になった解答が多くみられ、その比率は、小学2年生よりも高かった。これより、大学生は被乗数と乗数のちがいをほとんど意識していないか、または、乗法の計算式が「被乗数×乗数」で表されることを理解していないと推測される。
(p.46)
2006年:グレーゾーンの子どもに対応した算数ワーク 初級編2
[3] はこが 8つ あります。この中には チョコレートが 6こずつ はいって います。チョコレートは ぜんぶで なんこ あるでしょう。
しき□□6×8□□□□□
こたえ□□□こ□□□□□
[4] ふくろが 9こ あります。この中には りんごが 8こずつ はいって います。
りんごは ぜんぶで なんこ あるでしょう。
しき□□□×□□□□□□
こたえ□□□こ□□□□□
上記はいずれもp.77からです.[3]は左カラム下段,[4]は右カラム上段です.
関連:グレーゾーンの子どもに対応した,かけ算の出題
2005年:向山型算数授業法事典 小学2年
pp.76-77では,「おかしのはこが4つあります。1つのはこには,おかしが5こずつはいっています。みんなでなんこになるでしょう。」という教科書からの問題を取り上げ,「かけられる数とかける数が入れ替わった文章題」を扱います.問題解決学習だとここで,「4×5=20」と「5×4=20」の式を出させて比較するところ,本文では「4×5=20」が出ることなく,板書の図を書き写させて,「5×4=20」へと導いています.pp.78-79は,作問の授業です.教科書の出題は,「下のえを見て,3×4のしきになるもんだいをつくりましょう。」です.子どもたちが問題を作ったら,先生はそれを見て,寸評とともに「4点」「1点」「10点」といった個別評定をします.「10点」でなければ作り直します.2〜5の段のかけ算へと広げて、同様に子どもが問題を作り,先生が個別評定をしていくと,そのうち「12点」という点数が出て、子どもたちはびっくりします.それは「前時にやった「かけられる数」と「かける数」が入れ替わった文章題」です.
関連:2. 向山型算数授業法事典 小学2年
2005年:「計算の力」の習得に関する調査
- http://www.sokyoken.or.jp/kanjikeisan/keisan_h18.xhtml(デッドリンク)
- http://www.sokyoken.or.jp/kanjikeisan/pdf/2nen.pdf(デッドリンク)
◎ 6つのはこに,ケーキが8こずつはいっています。ケーキはぜんぶでなんこあるでしょう。
式の正答率は50.8%,答の正答率は81.3%です.3年生にも同じ出題があり,式の正答率は23.8%となっています.
2003年:どの子も伸びる算数力
「小さな子が、公園の砂場で遊んでいます。何人いるかなと数えてみると、6人いました。どの子も三輪車に乗ってきています。じゃあ、車輪の数は、みんなでいくつあるでしょう」
1回で文意が理解できない子には、2回でも3回でも、ゆっくりと語り聞かせるように繰り返し話してやります。問題の中身が分かったら、式を書かせてみてください。きっと、十中八九は失敗します。「ひっかかったわね。落とし穴にはまったわ」とおどけてやりますと、子どもはいぶかります。きょとんとしています。子どもはきっと「6×3=18」という式を書いているはずです。
(p.172)
2002年:日常生活の中で計算が活用できる子供の育成を目指した学習指導の一試み
- 伊藤宏: 日常生活の中で計算が活用できる子供の育成を目指した学習指導の一試み−「算数日記」を活用した3年「2位数×2位数」の授業実践を通して−. https://www.edu-c.pref.miyagi.jp/mnavidata/practice_research/01B0010.pdf
【問5】ここに4まいのふくろがあります。かずや君が,1まいのふくろにりんごを3こずつ入れました。りんごは,ぜんぶでなんこありますか。
① こたえを出すためのしきを書いてください。
② どうして,そのようなしきになったか,絵に書いて教えてください。
(p.5)
関連:教育評価論から見たかけ算の順序(2021.07) - かけ算の順序の昔話, 教育評価論から見たかけ算の順序―若柳小学校事例の別考察, 「計算の意味の理解」の調査における一考察
1999年:小学校学習指導要領解説 算数編
さらに,除法の逆としての乗法の問題,例えば「ひもを4等分した一つ分を測ったら9cmあった。はじめのひもの長さはいくらか。」のような場合にも,乗法が用いられることに着目できるようにする。
(p.91)
1993年:「2×3か3×2」の数学
- 伊藤武広, 荻上紘一, 原田実: 算数を教えるのに必要な数学的素養―「2×3か3×2」の数学―, 信州大学教育学部紀要, No.79, pp.15-17 (1993). http://ci.nii.ac.jp/naid/110000236964 https://researchmap.jp/kaz-mori/others/31061889/attachment_file.pdf http://www.avis.ne.jp/~uriuri/kaz/profile/Itohetal1993.pdf(デッドリンク)
小学校2年の算数でかけ算の導入の際に
(☆)「3枚の皿にリンゴが2個ずつのっている時全部でリンゴが何個あるか」
という類の問題が扱われる.これに関して著者の1人は次の様な経験を持つ.
著者の長男が2年生の時上記の問題に対して
「3×2=6」
と解答したところ,担任教師は「答えの6は正しいけれども,式は3×2ではなく2×3でなければならない」と指導した.長男は「そういうものか」と思ったようであるが,著者は早速担任にその理由を質問してみた.担任教師と著者とのやりとりは概略次のような内容であった.
1989年:小学校指導書 算数編
第2学年では,乗数が人数や個数などの簡単な場合について学習してきている。(略)「ひもを4等分した一つ分を測ったら15cmあった。はじめのひもの長さはいくらか。」(略)
(p.92)
1988年:算数 よい授業わるい授業
「4×6が正しいか、6×4が正しいか――かけ算九九論争」というタイトルの本文は,「某市立のF小学校の二年のテストに上のような問題が出された」から始まります(p.130).問題文は点線の箱囲みで,「6人の子どもに、1人4こずつみかんをあげようと思います。みかんはいくつあればよいですか。」と記されています.
関連:2013年はトランプ配り,1988年はアレイ
1984年:おかしなおかしな数学者たち
もう大分前のことになると思うが,あるとき私の所へ,名古屋から電話がかかってきた.そしてその電話の主はつぎの話を私にした.
「名古屋のある小学校で、算数の試験につぎの問題が出た。
ミカンを4つずつ6人の人に配りたいと思う。ミカンは全部でいくつあればよいか。
この問題に対して、大部分の子どもは、
4×6=24
個と答えたが、なかに一人、
6×4=24
と答えた子があったが、先生はこれを0点にしてしまった。
この先生の考えでは、問題の性質上、これは4掛ける6と考えるべきであって、6掛ける4というのはおかしい。したがってたとえ答えはあっていてもこれは0点であるということであったらしい。
ところがPTAの人たちは、答えがちゃんと合っているのに0点とはひどいといって騒ぎ出した」
ここまで話したその電話の主は
「ところで矢野先生は、4掛ける6がよくて、6掛ける4はいけないとお考えですか。それとも4掛ける6でも、6掛ける4でも、どちらでもよいとお考えですか」
と私の意見を求めた。
(pp.119-120)
と答えてもよいではないかという返事をして、私はようやく一時間の宿題を解いたわけであるが、一週間ほどのちに、遠山先生に以上のことをお話したら、
「矢野くんはやっぱり算数は素人だね。実際、矢野君の言うように考える子がときどきあるんだよ。われわれはこのような配り方を、カード式配り方と呼んでいるがね」
ということであった。
つまり、遠山先生のお考えによれば、いやしくも数学の教師たるものは、乗法の交換法則4×6=6×4に対してもここに述べたような二つの方法による説明を知っているべきである、ということであった。
(p.124)
1983年:算数つまずきの診断と治療
(4) かけざんの しきを かいて こたえを もとめなさい.
① 4こいりの せっけんの はこが 3はこあります.せっけんは みんなで なんこ はいっていますか.
しき( ) こたえ( )
② いろがみを 8人にくばります.1人に3まいずつくばると なんまいくばることに なりますか.
しき( ) こたえ( )
③ かぶとむしが 4ひきいます.かぶとむしの あしは 1ぴきに6本あります.あしは みんなで なん本ありますか.
しき( ) こたえ( )
④ 5dlいりの ジュースのびんが 8本あります.ジュースは ぜんぶで なんdlありますか.
しき( ) こたえ( )
(pp.112-113)
(4)の文章題では,②の問題で式に
ⓐ 3×8=24
ⓑ 3まい×8=24まい
ⓒ 3まい×8人=24まい
ⓓ 8×3=24
ⓔ 8人×3まい=24まい
などの式がみられた.どれも正答として扱ったが,ⓓⓔについては,1人あたり3まいずつ,8人の色紙のまい数を求めるのだから,式は,
(1まいの数)×(いくつ分)=(全体の数)
3まい × 8 = 24まい
と,被乗数は1あたりの数の「3」のほうがよいことを説明した.(略)
文章題についての誤答は意外に少なかったが,そのわけはかけ算ばかりの問題で,しかも乗数と被乗数を入れかえた式を書いても正答にしたためである.
(p.116)
1983年:さんすうの授業 第1階梯
(5)かけ算の文章題づくり
かけ算の意味が子どもに理解できているかどうかの最終的なツメです。意味がわかれば,問題がつくれるからです。そこで,「6×8の文章題をつくりましょう」と問題を出し,ノートに文章題をつくらせました。
〔子どもがつくった文章題〕
1) 1あたり量が先にきている問題
- 1はこにトイレットペーパーが6ロールはいっています。そのはこが8こあります。トイレットペーパーはなんロールありますか。
- 1ぴきの「なまず」の水そうに,えさの「めだか」を6ぴきずつ入れることになりました。「なまず」の水そうは8こです。さて「めだか」はなんびきいるでしょうか。
2) 分量が先にきている問題
- ねこが8ぴきいます。1ぴきにすずを6こつけると,すずは何こいりますか。
- 8びんにジュースが6dlあります。ジュースは何dlですか。
- 車が8だいありました。どの車にも人が6人ずついます。ぜんぶでなん人いるでしょう。
3) つまずいている例
- 1さつ8ページの本があります。その本が6さつあります。全部で本のページはいくつでしょう。
- ふねが6そうとまっています。人間が8人ずつのっています。ふねは,何そういるでしょう。
- (残り2例省略)
(p.176)
1978年:小学校指導書 算数編
- 文部省: 小学校指導書 算数編, 大阪書籍, 昭和53年5月, MEJ 1-7807.
第2学年では,乗数が人数や個数などのいわゆる分離量を表す1位数の場合について指導してきている。(略)「ひもを4等分した一つ分を測ったら15cmあった。はじめのひもの長さはいくらか。」(略)
(p.92)
1972年:6×4,4×6論争にひそむ意味
- 遠山啓: 6×4,4×6論争にひそむ意味, 科学朝日1972年5月号.
1972年1月26日の『朝日新聞』に小学校のテストをめぐる論争がのった。それによると,昨年の秋,大阪府松原市・松原南小学校の2年生のテストに,つぎのような問題があったという。
「6人のこどもに,1人4こずつみかんをあたえたい.みかんはいくつあればよいでしょうか」
これに対して何人かの子どもは,
6×4=24
と書いたが,その答案は,答えの24こにはマルがつけられ,式の6×4にはバツがつけられ,4×6と訂正されたという。
(p.114)
1972年:朝日新聞記事
「6人のこどもに、1人4個ずつみかんをあたえたい。みかんはいくつあればよいでしょうか」――昨年秋、大阪府松原市・松原南小学校の二年生の算数のテストで出された問題である。答案に「6×4=24こたえ24こ」と書いた子が何人かいた。結果は、答えの「24こ」はマルだったが、式の「6×4」にはペケがつけられ「4×6」となおされていた。これがきっかけで「6×4ではなぜいけないのか」という父兄と学校との間で、学校教育のあり方をめぐる論争に発展している。(略)
1972年:かけざんをやろう
問題文は「8ひき ならんだ 7ほしてんとう虫。ぜんぶで ほしは いくつ?」です.ここは7の段を使って解くことが期待されています.
参照した本は2012年3月10日 初版第1刷発行ですが,「本シリーズ「さんすう だいすき」は、ぽるぷ出版より1982年に刊行された『さんすう だいすき』第2版(全10巻、初版は1972年)を復刊したものです。」と奥付に書かれているので,1972年刊としました.
1971年:水道方式入門
〔練習もんだい〕
(略)
② 学校にはせいとが784人います。1カ月に1人が画用紙を25まいずつつかうとすると,この学校では1カ月に何まいの画用紙がいりますか。
(p.261.執筆者は岡田進)
1969年:東京都算数教育研究会の調査
- 花村郁雄: かけ算の意味と方法―つまずき事例―, 新しい算数研究, no.85, pp.19-22 (1978).
東京都算数教育研究会が昭和44年1月に東京都の2年児童約2,000人について行った調査によると,次のように報告されている.
〔問題〕8×6のもんだいをつくりました.よいものに○をつけなさい.
(1)( )みかんが一つのおさらに8こ,もう一つのおさらに6このせてありますが,みかんはなんこありますか.
(2)( )えんぴつを6本かいました.このえんぴつは1本8えんです.いくらはらえばよいですか.
(3)( )1まい6えんのがようしを8まいかいました.いくらはらえばよいですか.
この正答率は34.1%で,誤答率は61.5%,不答率は4.4%であったという.
(p.117)
1957年:算数科の教育心理
三年の指導
1. 必要な条件を抜き出して書かせる指導
問題1 おかあさんが,びわをおぼんにのせて,ぼくたち7人に下さいました。1人が6つずつたべたら,ちょうどなくなりました。はじめに,びわはいくつあったのでしょう。
問題2 はこづめのいちごがならべてあります。1つのはこには5こずつ,4れつにはいっています。いちごのかずはどれだけでしょう。
以上の問題を三年生の42名に回答させた。問題(2)では,ほとんどの子どもが5×4=20と正しく式に表現し,被乗数と乗数とを反対にして4×5=20としたものは,僅かに2名であった。問題(2)に対して問題(1)では,6×7=42としたものが22名で7×6=42と被乗数と乗数とを逆に書いたものは18名の多きに達した。その理由を探求してみると,乗法の文章題として与えられる問題は,問題(2)の形式の類が多くドリルさせられ,問題(1)の形式の類はその練習度が少ないので,しらずしらずの中に,乗法の問題では,文章中の初めに出て来た数を被乗数に,後から出て来た数を乗数にしたらよいのだというふうになっているからではないかということが考えられた。いいかえると,深く問題を読むことなしに,誤った先入観によって式化してしまう悪習慣がついているからであろうと思えた。
そこで,問題を深く読み,乗数と被乗数とを正確に理解させるために,つぎのようなことをした。
- さんすうのテストで3つまちがいました。1つ5てんびきだそうです。なんてんひかれるでしょう。
- こたえのめいすう……いくつ,なんてん
- かけられるかず……( )
- かけるかず……( )
答えの名数の正しいところを,○印でかこませ,かけられる数,かける数を記入させて立式させるようにした。
その結果,在籍42名中,被乗数と乗数とを逆にして式を立てたものは,僅かに5名であった。しかも,5名中,全部の問題(4題提出)を誤ったものは1人もなく,3問まちがったもの1名,あとは1問だけ誤っていた。一応成功したといってよいのである。
(pp.137-138)
2. 四年生の指導例
4年1組45名で,こう堂にいすをはこんでいます。1人が1こずつ4かい運ぶと,みんなでいすは,なんこ運ぶことになるか。
黒板に出てした子どもの解法には2つの型があった。
A 4こ×45=180こ
B 45×4=180
Aは正解であるが,Bは間違っているという意見が出て討論がはじまった。
「Aなら意味がわかるけど,Bでは意味がわかりません。45は人数だから180人になります。」
「Bでも180こになります。」
と2〜3の子どもが主張したが,根拠が薄弱でみんなを納得させることができない。そこで,教師はAの解法の意味をつぎのようにおさえさせた。4こ × 45=180こ……全体で運んだ数 ↓ ↓ 一人が運ぶ数 人数「Aの解き方が正しいことはわかりましたね。こんどはBの解き方がほんとうに間違っているのか。正しいとしたら,なぜ正しいのか。問題を読んで,1つ1つの数に当って,その意味をしっかり考えてごらん。」子どもたちはとうとう発見した。
45こ × 4=180こ……全体で運んだ数 ↓ ↓ 全体が1回 回数 に運ぶ数T「Aの解き方とBの解き方と,どう違うのでしょう。」
P「解く前の考え方がちがいます。」
A,Bの解き方を比較して話し合いながら,問題をとくときの大切な考え方として,つぎのようにまとめた。
- 見とおしをつける。
- それから計算にうつる。
A,Bの見とおしのつけ方のちがい。
A 1人が運ぶ数を考える。それを人数倍したら全体の数がでる。
B 1回にみんなが運ぶ数から考える。それに回数をかけると全体の数が出る。
この指導の後で,1日おいて次の問題を,見透しをまずノートに書いてから立式するように指導した。
四年生96名で,こう堂にいすをはこんでいます。1人が2こずつ4かい運ぶと,みんなでいすは,なんこ運ぶことになりますか。
1つの観点で解決に成功した子どもには,別な観点で解くように指示した。子どもたちが意識して見透しをつけるようにするためには,観点をたてることの指導の最初の段階において,教師は適切な指示を怠ってはいけない。このように観点をたてることの指導は,数の働きがわかることを基礎として,立式指導に関連させ,多方的解法をさせることによってその効果をあげることができる。
(pp.151-152)
関連:1. 算数科の教育心理
1951年:小学校学習指導要領 算数科編(試案)
三年の乗法九々の学習で,三の段がひととおりすんで,こどもたちは三の段の九々がすらすら唱えられるようになった。そこで,教師は次のようなテストを行って,こどもがかけ算の意味を理解して,九々を適用する力が伸びたかどうかを調べてみた。
問題 3人のこどもに,えんぴつを2本ずつあげようと思います。えんぴつがなん本いるでしょう。どんな九々をつかえばわかりますか。
どんな九々をつかうかという問に対して,3×2=6と答えたものが予想以上に多いことがわかった。これによってこどもは問題に出てくる数を,その数の意味を深く考えもしないで,出てくる順に書き並べ,その間に,かけ算記号を書き入れることがわかった。問題に出てくる数を頭の中にいったん収めて,演算の決定に導くように問題の場を組織だてる力が欠けているらしいことがわかった。そこで,その欠けていることについての再指導に入るわけである。
1941年:カズノホン 四
- 文部省: カズノホン 四, 日本書籍 (1941). http://dc.lib.hiroshima-u.ac.jp/text/metadata/1910
(3) 七人デ オハジキ遊ビヲ シテ ヰマス。一人ガ 五ツヅツ 出シマシタ。オハジキハ ミンナデ イクツ アル デセウ。
(p.23)
三番 「五七 三十五」の九九によつて解決させ得るであらう。
問題に於て,被乗数が後に来てゐる点で,一番・二番に比し,少しむづかしい感じがするであらう。
(カズノホン 四 教師用, p.53. http://dl.ndl.go.jp/info:ndljp/pid/1439928/30)
関連:カズノホンの掛算九九学習
1936年:尋常小学算術書活用と補充
- 高木佐加枝: 尋常小学算術書活用と補充 第2学年 上巻, 賢文館 (1936). http://kindai.ndl.go.jp/info:ndljp/pid/1462874
○ 10人の人が電車に乗つた,一人分は4錢づゝであると,全體で幾らになるか。
(p.295)
関連:昭和初期の《BA型》
1936年:緑表紙教科書
- 山澤晴子: 尋常小学算術の内容の新たな教材化の可能性, 上越数学教育研究, 第23号, 上越教育大学数学教室, 2008年, pp.143-156. http://www.juen.ac.jp/math/journal/files/vol23/yamazawa08.pdf
【第二学年】
掛け算九九
・2の段スイカ ガ ヨク 出来タ ノデ,五ケン ノ シンルイヘ,二ツ ヅツ アゲマシタ。ミンナ デ イクツ アゲタデセウ(上 P.57)
(p.150)
1933年:算術科教育測定報告書 事実問題の部
- 東京市教育局(編): 算術科敎育測定報告書(事實問題の部), モナス (1933). http://dl.ndl.go.jp/info:ndljp/pid/1464965
(1) 子ドモ8人 ニ エンピツ ヲ 4本ヅツ ヤルニハ ミナデ イク本 イリマスカ。
(p.22, コマ番号19.答えのみ)
(5) 48人ノ生徒ニ6銭ノ筆ヲ1本ヅツ買ツテヤルトソノ代ハイクラカ。
(p.24, コマ番号20; p.30, コマ番号23; p.40, コマ番号28)
(10) 一サツノ本ガアル。コレヲ5日ニヨンデシマフニハ毎日35ページヅツヨメバヨイ。コノ本ハ幾ページアルカ。
(15) 生徒ヲ同ジヤウニ4組ニ分ケルト1組ガ16人ニナル。生徒ハ幾人カ。
(p.25, コマ番号20; p.31, コマ番号23; p.41, コマ番号28)
尋三 事實問題 No.1 (尋四 No.1 尋五 No.1)審査例
例トシテ問題(5)ヲ採ル
○ (イ)6銭×48=288銭 答 2圓88銭 (ロ)6×48=288 答 2圓88銭
× (イ)48×6=288 答 2圓88銭 (ロ)48×6銭=288銭 答 2圓88銭 (ハ)48人×6銭=288銭 答 2圓88銭
(p.139, コマ番号77)
関連:https://twitter.com/temmusu_n/status/1053137616122470400 https://twitter.com/flute23432/status/1188484688580509697
1909年:広算術教科書
- 高木貞治(編著): 広算術教科書. 開成館 (1909). [asin:B0090YGCH2] http://kindai.ndl.go.jp/info:ndljp/pid/826655
12. 東京ヨリ横濱マデノ鐵道距離18哩ナリ。三等乗車賃金一哩毎ニ一錢六厘五毛ナルトキハ,此賃金幾許トナルカ。
(p.60)
関連:高木貞治『広算術教科書』に見る,因数の順序,基準量が後に示された問題,内包量とパー書き〜1960年代,1970年代,1980年代の記述より
*1:なので,かけ算は出てこないのですが,かけ算の素地になる学習内容であることから,ここに載せました.