算数教育・資料集（書籍：2000〜2009年）

目次

• 算数・数学科重要用語300の基礎知識
• どの子も伸びる算数力
• 使える算数的表現法が育つ授業
• 板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉
• 徹底反復文章題さかのぼりプリント
• 新しい発展学習の展開算数科 (小学校1〜2年)
• 確かな学力を育てる算数科学習指導略案集 低学年編
• グレーゾーンの子どもに対応した算数ワーク
• 算数科:授業と板書のアイデア12か月 1〜3年編
• オトナのための算数・数学やりなおしドリル
• 歌で必ず暗記できる新版9×9のほん
• 算数再入門
• かけ算とわり算 (算数の本質がわかる授業)
• 「教えて考えさせる授業」を創る
• 教育評価
• 小学算数なっとくワーク2年生
• 算数教育指導用語辞典
• 算数好きにする教科書プラス 坪田算数2年生
• 田中博史の算数授業のつくり方
• 中学入試をめざすトップクラス問題集算数小学2年 徹底理解編
• 必備!算数の定番授業 小学校2年
• ドリルの王様２年の文しょうだい
• 誰もができる子どもに活用力をつけるワクワク授業づくり
• 遠山啓エッセンス〈3〉量の理論
• 時代を拓く子どもが育つ授業
• 小学校 算数科の指導

算数・数学科重要用語300の基礎知識

算数・数学科重要用語300の基礎知識

乗法の意味を指導するときや，かけ算九九の指導をするとき，乗法の交換法則の指導は慎重に扱うべきである．かけ算の意味の指導では，交換法則が容易に説明できないからである．4円×8と8円×4とでは，式の意味が同じではない．式の意味が理解され，児童が法則を意識できるようになってから指導する方がよい．かけ算九九の指導を終え，ある程度計算できるようになった段階で指導しても遅くはない．
(p.175)

ヴェルニョー(Vergnaud, G.)は，乗法・除法を成立させている最も基本的な操作や場面を，2つの量空間の間の比例関係から捉えようとする．乗法は，導入に際しては同数累加の簡便法として意味付けられることが多いが，ここではヴェルニョーの考え方と図式を利用して乗法の意味を捉えてみる．
(1) スカラー関係に基づく乗法
(2) 関数関係に基づく乗法
(3) 量の積に基づく乗法
(p.187)

★◆☆

どの子も伸びる算数力

どの子も伸びる算数力

「小さな子が、公園の砂場で遊んでいます。何人いるかなと数えてみると、6人いました。どの子も三輪車に乗ってきています。じゃあ、車輪の数は、みんなでいくつあるでしょう」
1回で文意が理解できない子には、2回でも3回でも、ゆっくりと語り聞かせるように繰り返し話してやります。問題の中身が分かったら、式を書かせてみてください。きっと、十中八九は失敗します。「ひっかかったわね。落とし穴にはまったわ」とおどけてやりますと、子どもはいぶかります。きょとんとしています。子どもはきっと「6×3＝18」という式を書いています。
この式なら、言葉で言うと、6人ずつのかたまりが3つあるということになります。そして、答えが18人ということになってしまうのです。
この問題では、車輪の数はみんなで何個あるのかを問いかけているのです。三輪車に車輪が3個あります。その三輪車が6台あると、みんなで車輪の数はいくつかということを聞いているのです。1台ずつに3つのかたまりがあって、全部で6つある。じゃあ、車輪の数の合計はいくつになるのかというのが、求める答えです。
けっして6×3ではありません。3個が6つあるのですから、式は「3×6＝18」と書かなければなりません。
(pp.172-173．《ＢＡ型》)

★☆☆

使える算数的表現法が育つ授業

使える算数的表現法が育つ授業 (算数的表現力を育てる)

このような経験をしたあとで，これらの言葉を式にするのである。
3こと2こ⇒　3＋2
3こが2こ⇒　3＋3
でも「3こが2こ」と束ねた言い方では，3と2という数字があるのに，式になると2が出てこない。
そこで，
3こが2こ　⇒3×2
とかくことを教えるのである。
突然かけ算の式を見せられるのではなく，このようになんとか，束ねた言い方を考えるという意識が働く中で，かけ算の式に出会わせることができた。
この言い方は，この後，数が増えると本当に便利になってくる。
3こと3こと3こと3こと3こ　⇒　3こが5こ　⇒　3×5
というようにである。
ここにも，かけ算の式のよさがある。
(p.71)

板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉

板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉

ヨットが8そうあります。同じ人数ずつ*1のっています。ぜんぶで何人いるでしょうか。
(p.43．《ＢＡ型》)

正しくは5×4なのであるが，問題文の中では，4の方が5よりも先に使われているので，4×5だと考える子がいるようである
(p.48．上の引用の解説．)

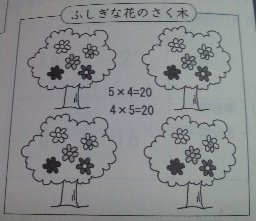
4本の木に、それぞれ5こずつリンゴがなっています。リンゴはぜんぶでいくつでしょうか。
〈しき〉
5×4＝20
4×5＝20
どっちが正しいのかな?
(p.49．《ＢＡ型》)

ふしぎな花のさく木

このような問題を扱うと，次のような場面を考えてくる子がいる。「4×5」でも「5×4」でもどちらでも答えが求められる場面である。
(p.49．《複数解》)

おかしがはこに入っています。何こあるでしょうか。
（図省略）
7×4＝28, 4×7＝28
(p.57．《複数解》)

(pp.46-47)

★☆☆☆

徹底反復文章題さかのぼりプリント

徹底反復文章題さかのぼりプリント〈算数〉―基礎学力向上プリント (小学校2年)

8人のこどもに、5ひきずつ、メダカをあげました。メダカは、ぜんぶでなんびきでしょう。
（p.106．この本で唯一の《ＢＡ型》）

（しき）5ひき／人×8人＝40ぴき　（こたえ）40ぴき
(p.128)

新しい発展学習の展開算数科 (小学校1〜2年)

新しい発展学習の展開算数科 (小学校1~2年) (教育技術MOOK)

これまでのたし算やひき算の式では、式の中で用いている数はすべて同じ種類のものだった。たとえば、りんごが8こあって新たに4こもらうというようなとき、8＋4＝12としてりんごの総数を答える。このとき登場する8、4、12という数は、すべてりんごの数である。
これに対してかけ算の式では、登場する数が2つの種類になる。
たとえば、次のような場面を4×3＝12とあらわすのだが、りんごの数は4と12だけであり、3はいくつ分あるかをあらわす数となっている。
（図：省略）
これがまず大きな違いである。このような演算を単項演算という。この場合は、3×4と4×3の意味は異なる。これが抽象的な数になり2つの数が対等になったとき、二項演算になる。このときから交換法則が成立するようになる。
(p.86)

シールの色にこだわる必要はない。ただ、ひと塊になる量だけは同じ色にしておきたい。
この段階では、9×3と3×9はまだ別のものだからである。(略)
(p.89)

確かな学力を育てる算数科学習指導略案集 低学年編

確かな学力を育てる算数科学習指導略案集 低学年編

（問題文の左に図：省略）
みかんのふくろが4つあります。
1つのふくろには，みかんが5こずつはいっています。
みんなでなんこになるでしょう。
(p.110．《ＢＡ型》)

2，3，4，5の段の九九を使って，基準量が後に示された問題を解く。
(p.110)

グレーゾーンの子どもに対応した算数ワーク

医学と教育との連携で生まれたグレーゾーンの子どもに対応した算数ワーク (初級編2)

[1] あめを　一人　４こずつ　６人に　くばります。あめは　ぜんぶで　何こ　いるでしょう。
[2] ３人ずつ　のった　ボートが　７そう　あります。ぜんぶで　なん人　のって　いるでしょう。
[3] はこが　８つ　あります。この中には　チョコレートが　６こずつ　はいって　います。チョコレートは　ぜんぶで　なんこ　あるでしょう。
[4] ふくろが　９こ　あります。この中には　りんごが　８こずつ　はいって　います。りんごは　ぜんぶで　なんこ　あるでしょう。
[5] 本を　一日に　６ページずつ　読むのを　一しゅうかん　つづけました。ぜんぶで　なんページ　読んだでしょう。
[6] 本を　一日に　４ページずつ　読むのを　一しゅうかん　つづけました。ぜんぶで　なんページ　読んだでしょう。
(p.77)

★

算数科:授業と板書のアイデア12か月 1〜3年編

授業力アップ!算数科:授業と板書のアイデア12か月 1~3年編

かけ算のよいところ

• かんたん
• いくつぶんか すぐわかる．
• たくさん かかなくていい．

(p.65．増田朱美：かけ算の式と意味を知ろう)

本時では，いくつ分の量が先に，基準量が後に示された適用題を扱うが，子どもたちは数値の与えられた順に立式してしまいがちである。そこで，題意をとらえ，基準量が何なのかを判断して正しく立式できるようにするために操作活動を取り入れる。問題場面を読み，基準量をおはじき，いくつ分をカップを用いて表すことによってかけられる数とかける数の意味をしっかりとらえさせたい。
(p.67．瀧崎美保子：なんのいくつぶんかをかんがえよう)

おかしのはこが5つあります．1つのはこにはおかしが4こずつはいっています．みんなでなんこになりますか．
でてきたじゅんばんに かけちゃだめ
かけられる数 かける数には いみがあるよ
(同)

オトナのための算数・数学やりなおしドリル

オトナのための算数・数学やりなおしドリル

2×3と3×2は同じ答えですが、考え方が違います。3組のカップルが映画館へ行ったとき「ペアシートが3席」と「3人用シートが2席ある」のでは違いますね。かける数、かけられる数の関係には、ちゃんと意味があるのです。
(p.14)

歌で必ず暗記できる新版9×9のほん

9×9のほん―歌で必ず暗記できる [CDつきえほんシリーズ] ([バラエティ])

「みんなで 5にんね! あめを 2こずつ クッキーを 3まいずつ 配りましょう。」
「あめは ぜんぶで 2こ×5にん・・・ 2×5＝10こ いるね!」
「クッキーは ぜんぶで なんまい いるかな? 3まい×5にん・・・ 3×5＝15まい!」
(pp.21-22，こんなとき9×9（くく）がだいかつやく)

算数再入門

算数再入門―わかる、たのしい、おもしろい (中公新書)

9 掛け算について

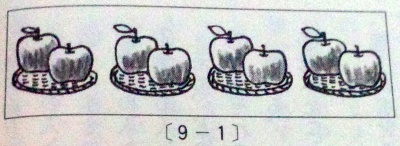
「左の絵にはリンゴがいくつありますか?」と問えば、8個という答はすぐに返ってくると思われます。しかし、このリンゴの数え方にはいろいろあるでしょう。「1、2、3、4……」と1つずつ順に8まで数える人もいれば、「2、4、6、8」と2個ずつ数える数え方をする人もいることでしょう。
この「2個ずつ4つある」という考えが、掛け算の素地と言えます。
私たちの身の周りには、同じ数ずつあるものがたくさんあります。6個パックに入った卵、12本ずつ箱に入った鉛筆など、すこし探せば同じずつまとまっているものがすぐに発見できるでしょう。その総和を求めるときに、「何個のいくつ分」ととらえるから、掛け算の思考が始まります。掛け算を教えるときは、「2＋2＋2＋2」というように、同数累加（同じ数ずつ足すこと）から始まり、「2個ずつの4個分」という考えを理解した上で、「（1つ分の大きさ）×（いくつ分）＝（全体の大きさ）」という掛け算（乗法）の意味を表した「言葉の式」として一般化した式で考えるようになります。この式はやがて「（基準量）×（割合）＝（割合にあたる量）」へと発展し、中学校では、多項式の項である単項式の意味になります。例えばという二次方程式も多項式ですが、この多項式の項であるを表すやを表すや単独の文字や数字のはすべて単項式となります。
また、「倍」という関係を表す言葉も、日常的に使われています。「倍」とは「ある量を基準とする大きさで測ったとき、基準とする大きさのどれくらいに当たるか」を表しています。図のリンゴ8個は、2個ひとまとまりのリンゴの4倍です。つまり、「倍」は、基準とする大きさを1としたとき、ある量が基準のいくつ分に当たるかという、割合の1つの表現と見ることができます。
(pp.40-41)

★

かけ算とわり算 (算数の本質がわかる授業)

かけ算とわり算 (算数の本質がわかる授業)

文章問題として、「いちごをお皿に４個ずつ載せます。それと同じものを３皿分作ります。いちごは全部でいくつあればよいですか」などを「国語式」と表現すれば、「４個／皿×３皿＝12個」は「算数式」、そして「４×３＝12」は「数字式」といえるでしょう
式を「算数式」と「数字式」に分けて考えれば、より現実の場面をとらえやすいのは「算数式」です。
かけ算を（１あたり量）×（いくつ分）＝（全体量）と決めて目前の現象を見たとき、「４個／人×３人＝12個」と「３個／人×４人＝12個」では、全体量は同じでもようすは違います。
(p.18)

「教えて考えさせる授業」を創る

「教えて考えさせる授業」を創る―基礎基本の定着・深化・活用を促す「習得型」授業設計 (教育の羅針盤)

「わり算とは，かけ算の逆であり，全体量と分ける人数がわかっているときに1人分の個数を求める『等分除』お，全体量と1人当たりの個数がわかっているときに何人に分けられるかを求める『包含除』がある」ことは，すでに述べたとおりです．
これを教えるときに，図3・1のようなアレー図を使うことを私は提案したことがあります．アレー図は，小学校2年生でかけ算を教えるときによく使われるのですが，なぜか，わり算を教えるときにあまり利用されないのです．等分除と包含除の対称性を理解するにも非常に便利なツールのはずです．
(pp.96-97)

「12個のクッキーを3人で同じ数ずつ分けると1人分はいくつでしょう」という問題に対して，私の扮するワン太君は，「たし算もひき算もかけ算も知らない．数を数えることしかできないけれど，答えを求められる」のです．
(p.98)

教師の演示を見て，自分でも具体的に操作してみることによって，等分除と包含除の違いを意識してもらうのがねらいです．
(p.100)

そのうえで，「これはワン太君のやり方だったけれど，みんなは，ワン太君と違って，かけ算九九を知っているね．すると，1個ずつ配らなくても，答えが出せないだろうか」ともっていきます．つまり，図3・1のようなアレー図で，全体の個数12個と人数3人（横の長さ）がわかっていれば，「３×□＝１２」で1人分4個が求まります．また，全体の個数12個と1人分の個数4個がわかっていれば，「４×□＝１２」で人数3人がわかります．ここは理解深化課題として考えさせる展開にもできるでしょう．
(p.100)

★☆

教育評価

教育評価 (岩波テキストブックス)

たとえば，「乗法（かけ算）の意味理解」にかかわる実践を例にあげれば，「生活知」（加法の延長に累加――3×2＝3＋3――として乗法をとらえている状態）と「科学知」（「一あたり量×いくつ分＝全体量」として乗法をとらえること）の競合関係をいかに教育的に組織するのかという課題が成立する．この場合，何よりも実践者に意図されていることは，「生活知」の限界（乗数が大きくなれば累加は実際上困難）と「科学知」の有効性とそのための条件（あるものが均等配分されている場合には「一あたり量」と「いくつ分」を確定できれば「全体量」がわかる）を子どもたちが納得できる問題状況を設定することである．
(p.120)

それでは，「乗法の意味理解」を例として，さらに具体的に説明してみよう．まず乗法の意味としては，正比例型（一あたり量×いくつ分＝全体量），直積型（面積），倍比率型（倍），累加型（たとえば3＋3＋3）の4通りがあることを確認しておこう．しかしながら，乗法が後の微分や積分の基礎になるといわれる場合には，その意味内容として正比例型が重要となる．つまり，数学教育における乗法の核心的な意味は，「加法」の延長（累加を簡単にしたもの）にあるのではなく，均等分布を前提として異なる次元の量（一あたり量といくつ分）によって構成されるところにある．
(pp.155-156)

情報過多問題
牡鹿には角が2本ある．大人になるとその角に枝角が6本生える．牡鹿の角の大きさは5フィートである．さて，大人の牡鹿の枝角は何本か．
情報不足問題
象の背の高さは13フィートである．象は，毎日，干し草やフルーツや野菜を130ポンド食べる．象は3日間で干し草を何ポンド食べるのか．
(p.157)

パフォーマンス評価の一種である「作問法」（この場合は「算式法」）では，「4×8＝32となるようなお話をつくってください．そして，そのお話を絵で描いてみましょう」という例があげられるであろう．(略)
この場合の採点基準としては，「乗法の意味内容を踏まえたお話であるか」（正比例型，直積型（面積），倍比率型となっているか），「乗数と被乗数の意味が区別されているか」（とくに正比例型では「4」は「一あたり量」，「8」は「いくつ分」と区別されているか），「お話が現実的であるか」(略)，「お話と絵が一致しているか」を考えておけばよいだろう．(略)
(p.158)

このパフォーマンス課題では，「4.十分な達成――このプラン作成のために乗法を使う．3.実質的に達成――示唆を得て，このプラン作成のために乗法を使う．2.部分的な達成――プラン作成にあたって乗法で時々つまずく．1.未達成――このプラン作成のために乗法をつかわない」というルーブリックが提案されている．
(p.159)

小学算数なっとくワーク2年生

小学算数なっとくワーク2年生

(p.99)

2-①え　②う　③い　④あ
①と④が逆になってしまうことがあります。「いくつのまとまりが」「何組あるか」で正しく式を立てられるようにしましょう。
(解答・解説p.19)

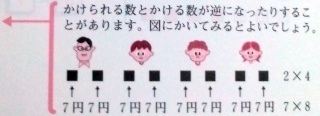
1まい7円の 色紙を，4人に 2まいずつ 買ってあげます。ぜんぶで いくらに なるでしょう。
(p.109)

しき　2×4＝8　7×8＝56
答え　56円

(解答・解説p.20)

(解答・解説p.20)

算数教育指導用語辞典

算数教育指導用語辞典

計算法則に関する注意事項
数の拡張では，三つの計算法則の確かめが必要であったが，これはあくまでも形式であって，これと離れた具体的な場面では注意すべきことがある。
例えば，交換法則に関しては，同じ加法でも合併なら交換が可能であるが，追加（増加）の場合では交換は不可能である。例えば，ミカンが5個あっても3個もらうと8個になるということから，3個もらって5個あってというのは意味が曖昧になってしまう。不用意に交換すると時間差を無視したりすることになる。
また，乗法で，被乗数と乗数を交換しているのは，2次元的な面積の場合が，縦横同じ種類の者が並んでいる人間とかおはじきなどの数を求める場合はわかりよい。
ただし，この場合でも，被乗数と乗数を交換したとき，その基準量をどうとらえたか，操作の観点をどこに置いたかをよく考え，その違いをはっきりとつかんでおかねばならない。同数累加や倍概念で操作する1次元的な乗法では，安易な交換は許されない。
例えば，三つの皿にみかんが2個ずつあるとき，みかん全部の個数は2×3で求められる。しかし，皿の数三つにみかんの数2個をかけて3×2というのは意味がなく，このような具体的な場面で2×3が3×2に等しくなることを理解させるのは，かなり無理があると考えられる。
(pp.18-19脚注)

かけ算の式
数量に対応して，かけ算の式を考えるときは，例えば，6×8のかけられる数6と，かける数8には異なる意味が対応している。
（かけられる数）　（かける数）　（積）
6　×　8　＝　48
（作用を受けるもの）　（作用を及ぼすもの）　（結果）
しかし，結果を求める計算や，その式がどんな数を表すかをみるとき*2は，6×8も8×6も同じ結果を表していると考える。
(p.189脚注)

算数好きにする教科書プラス 坪田算数2年生

算数好きにする教科書プラス 坪田算数2年生 (TEXT BOOK PLUS)

まっすぐな道にはたが立っています。
はたは6本です。
はたとはたの間は、どこも8mです。
はたのはしから、はしまで、何mでしょう。

さっそく、問題が解かれる。
(1) 6×8＝48(m)
(2) 8×6＝48(m)
(3) 8×5＝40(m)
(1)は二重の誤りで、式の表現が一つ分に当たる数といくつ分に当たる数を書く順が約束に合っていないし、間の数も違う。(2)は間の数を考慮していない。(3)が正解。子供の意見で徐々にこれが明らかになるように話を聞く。
(p.73)

田中博史の算数授業のつくり方 (プレミアム講座ライブ)

田中博史の算数授業のつくり方 (プレミアム講座ライブ)

例えば，次のような文章題を考えさせてみます。「船が５そうあります．１そうに４人ずつ乗ることにします。」このような問題文になっていると子どもは必ず式を間違えますよね。「５×４」と書きます。今まで文の中に出てきた順番に数を使って式を書くだけで，ずっと丸をもらえていた子たちは，必ずこういう問題で引っかかります。
(p.62．《ＢＡ型》)

★◆

中学入試をめざすトップクラス問題集算数 小学2年 徹底理解編

トップクラス問題集算数小学2年―中学入試をめざす 徹底理解編

〈乗法の式のたて方〉
「5枚のお皿に柿が3個ずつのっています。柿は全部で何個ありますか。」というような問題では，問題に出てくる数字の順に「5×3＝15」という式を書いてしまう場合があります。これは，問題の場面をしっかりイメージしていなかったり，乗法の式の意味を十分理解していなかったりするためにおこると考えられます。そこで，問題文を読むときに，「1つ分の大きさ」に当たる数を○で，「いくつ分」に当たる数を□で囲むように指示し，問題場面を具体的にイメージしているか，確認してみましょう。乗法の式では，初めに「1つ分の大きさ」を表す数を，次に「いくつ分」を表す数を書くことを理解できるようにしていくとよいでしょう。
(答えと解き方 p.27．《ＢＡ型》)

必備!算数の定番授業 小学校2年

必備!算数の定番授業 小学校2年 (活用力の基礎を育む授業ベーシック)

「かけ算を使って表せることが、この教室に見つけられるかな?」
「あるよ。このロッカーは4×3＝12だよ。」
「4×3＝12の12は、このロッカーでいうとどこにあるのかな?」
「このロッカー全部の数」
「では、4は?」
「この縦の4つ」
「たし算にすると、どうなるかな?」
「4＋4＋4＝12」
このロッカーの数のように縦横に並んでいて捉え方が2通り（この場合は4×3＝12と3×4＝12）ある場合は、ここであえて、違うたし算の表し方を問いたい。それをたし算で表させることで“単位とする大きさ”をかけられる数に表すことを明確にしていく。
「このロッカーから、他のたし算を考えた人はいるかな?」
「私は3＋3＋3＋3＝12を考えました。横の3個をひとまとまりにしました」
「こういう場合はかけ算にすると、3×4＝12となります。足し算にしたときに何回も足される数をかけ算の一番左（かけられる数）に書きます。」
(pp.48-49)

おまんじゅうが24こ入った箱

●●●●●●
●●●●●●
●●●●●●
●●●●●●
4×6＝24

●●●●●●●●
●●●●●●●●
●●●●●●●●
3×8＝24

●●●●●●●●●●●●
●●●●●●●●●●●●
2×12＝24

●●●●
●●●●
●●●●
●●●●
●●●●
●●●●
6×4＝24

●●●●●●●●●●●●●●●●●●●●●●●●
1×24＝24

●●●●　　●●●●
●●●●　　●●●●
●●●●　　●●●●
3×4×2＝24

(p.113)

「だったら、6×4もあるよ。」
「でも、それは4×6と同じだよ。」
「こうやって箱を回せば同じだもの」
交換法則を、箱を使って確認する。
(p.112)

ドリルの王様２年の文しょうだい

ドリルの王様　２年の文しょうだい

[6] 9人の 子どもに，いろがみを 3まいずつ くばります。いろがみは なんまい あれば よいでしょう。
しき（　　　　　　　　） こたえ（　　　　）
(p.38)

[6] しきを9×3＝27としてしまうまちがいがみられます。「3まいずつの9人ぶん」なので，もとになる数は3です。3×9と9×3では，しきのいみがちがうことをりかいしましょう。
(p.88)

9　えんぴつを，1人に 4本ずつ 6人に くばりました。
1人に 7本ずつ くばるには，あと なん本 あれば よいでしょう。
① 7本ずつ くばるには，1人に なん本 たりないでしょう。
② 1人に たりないぶんに 人数を かけて，あと なん本 あれば よいかを もとめましょう。
(p.52)

誰もができる子どもに活用力をつけるワクワク授業づくり

誰もができる子どもに活用力をつけるワクワク授業づくり―第2回RISE授業実践セミナーの報告

(1) おかしが、1枚のさらに2個ずつのっています。さらは3枚あります。
(2) さらが3枚あります。1枚のさらには、おかしが2個ずつのっています。
この文を式で表すと、どちらも「2×3」になるのだが、子どもに立式させると、(2)を「3×2」としてしまう間違いが見られる。文に出てきた数を、そのままの順番でかけ合わせるという間違いである。文を読み取り、具体的な場面をイメージできなかったことが、間違いの原因の1つと考えられる。
(p.67．《ＡＢ型》《ＢＡ型》)

┌─┐┌─┐┌─┐┌─┐
│□││□││□││□│
│△││△││△││△│
│○││○││○││○│
└─┘└─┘└─┘└─┘

○「4×3にも見える」という声が出てくると予想される。それは、箱の枠を取り払い、新しいかたまりをつくることで見えてくるものである。
(p.69．《複数解》)

遠山啓エッセンス〈3〉量の理論

遠山啓エッセンス〈3〉量の理論

(略)整理すると，3用法は次のようになります。
　　　　内包量 ＝ 総量÷容量　――第1用法
　　　　総量 ＝ 内包量×容量　――第2用法
　　　　容量 ＝ 総量÷内包量　――第3用法
(略)
小学校2年生で，かけ算を整理するときに，このようにしたほうがいい。たとえば，
　　　　2×3
を数えるときに，いままではウサギが3匹いて，それに耳が2こずつついているとしていたのですが，しかし，あれはウサギという容れもののなかに耳が入っているわけではありません。ウサギのからだに耳がついているのですから，ウサギを容れものとは考えにくい。容量とは考えにくい。あれは，ほんとうは生きたウサギではなくて，ウサギのお面をつくるのに，部品としての耳が２ついるという意味だったのです。お面だったのがだんだん誤解されて，生きたウサギになってしまった。生きたウサギは，子どもにとってたしかに親しみやすいから，最初に出てくるものとしてはいいのですが，シェーマとしてはあまりうまくない。やはり，2×3のシェーマとしては，「1箱に何かが2つずつ入っているものの3箱分」としたほうがわかりやすい。箱だったら容量ですから，この先，ずうっとこのシェーマで行くことができます。そういうように考えたほうがいいのではないか。それで，今度の『わかるさんすう』（麥書房）の改訂では，この方針にそって変えたわけですが，みなさん，だいぶ反発されたようです。おおいに反発してくださって結構です。意見を出してもらわないと，議論は発展しませんから。
しかし，シェーマとしてはこのほうが発展性がある。3のほうは容量といったほうがいい。だから，2のほうはタイルで表示するけれども，3のほうは箱になっているのです。このようなシェーマでかけ算を定義するのです。いままでの
　　　　「タイル×タイル」
というのは，子どもにはなかなかわからない。
　　　　「外延量×外延量」
という計算は，面積などにたしかにあるわけです。しかし，それは一般性をもっていなくて，非常に特殊な物です。それでやはり，
　　　　総量＝内包量×容量
という考えに変えたわけです。いままでも，「÷3」のようなわり算をやるときは，3のほうは箱になっていたわけですから。
(pp.154-155)

★

時代を拓く子どもが育つ授業

時代を拓く子どもが育つ授業―新学習指導要領は子どもに何を求めているか (算数授業研究シリーズ)

かけ算を習ってしばらくしてから，次のような問題を出すと，多くの子どもたちは，問題文に出てきた順番通り立式しようとする。

ドーナツのはこが 4つ あります。
1つのはこには ドーナツが 5こずつ 入っています。
ドーナツは ぜんぶで なんこ でしょう。

4×5＝20

しかし，この式に異を唱える子も出てくる。
「だって，『ずつ』という言葉が後から出てきているよ。」
「図をかいてみればいい。」
そういって，この問題文は，

5×4＝20

の式が正しいと主張してくる．
式の順番などどうでもよい，答えが正しければいいじゃないか，という大人もいる。しかし，表現の手段としての「式」を考えた場合，それはまずい。
実はこのクラスの子どもたちは，かけ算の学習当初から，「○×△」は，「○のまとまりが△つ分」という意味を算数の言葉で表したもの，というように式＝表現ということを繰り返し学んできた。「ドーナツを4つずつ5個に入れる」場合と「5こずつ4箱に入れる」場合はまったく違うことが意識できる子どもたちなのである。
(pp.21-22．《ＢＡ型》)

小学校 算数科の指導

小学校 算数科の指導

おかしの　はこが　３つ　あります。
１つの　はこには　おかしが
６こずつ　はいって　います。
みんなで　なんこに　なりますか?

しきは、３×６かな?
６×３かな……
(同上, 右囲み)

(p.69．《ＢＡ型》)

(2) かける数とかけられる数
一般に，具体的な問題は，「基準量」と「いくつ分」が，この順番で示されているので，演算の意味を考えもしないで乗法の式に表す傾向がある．乗法の演算の意味を深めるためには，次のようなかける数とかけられる数が入れ替えた問題を取り扱い，確かな乗法の演算の意味理解を図ることが大切である．
(p.69)

（最終更新：2013-02-21 早朝）

*1:「同じ人数ずつ」の下に波線と「3人ずつ」があります．これらは，板書において，問題文を書いた後で書くものとされています．

*2:出題者が「6×8」を提示して，「答えを求めましょう」「これと答え（積）が等しくなるようなかけ算の式を，九九の表から見つけましょう」などを出題する場面と思われます．前の段落の「数量に対応して，かけ算の式を考えるとき」との違いに注意したいところです．