わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

Towards Japanese Multiplication Instruction

5×3

Table of Contents

  1. Introduction
  2. Multiplication Understanding and Elementary Math Education in Japan
  3. Dealing-out
  4. Product-based Problem and Product-oriented Solution
  5. Multiple-based Problem and Multiple-oriented Solution
  6. Which will it be?
  7. To Support the Understanding of "Number of Objects in Each Group"
  8. Order-of-multiplication Dispute
  9. Conclusions

1. Introduction

In Japan, teachers strenuously teach the multiplication to their pupils in the second grade. Main activities are to write a math sentence such as "2 x 3" or "2 x 3 = 6" for a given situation and to recite the multiplication table called "kuku". Some of the children can hardly wait the central role on the mathematics learned in that year.

When the pupils study to a certain extent, they solve a word problem in a special form.

The problem statement is "There are 5 dishes and 3 apples are on each dish. How many apples do you have altogether?" There is attached an answer column for the math sentence and the conclusive quantity. The pupil wrote in "5 x 3 = 15" and "15 apples". After that, the sheet was red-penciled so that the total number might be right but the sentence wrong; the correct sentence is "3 x 5 = 15". Note that in Japan a circle and a cross are marked in a red pen to indicate the correct and the incorrect answers respectively.

I am in sympathy with this way of math education, which takes good care of math sentences apart from the correctness of answers such as pure or concrete numbers, through the books and the research papers about multiplication instructions.In other words, I am proud of the Japanese math education today.

In this article, we trace a path through the decision with which they regard "3 x 5" as correct and not "5 x 3" in the above example. To do so, I introduce the standard understanding of multiplication in Japan, the criticisms, two ways of thinking of multiplication, and the basis activities including "skip counting".

2. Multiplication Understanding and Elementary Math Education in Japan

In this section I would like to show the contemporary education of Japan with regard to the introduction of multiplication.

Pupils understand the multiplicative sentence in which the multiplicand lies to the left of the symbol "x" and the multiplier the right, typically in the second grade. The multiplicand means the "number of objects in each group", while the multiplier indicates the "number of groups" [Yoshida 2009]. They coincidentally learn about how to write the math sentence and about how to compute the product through various situations and problems.

In a class, a pair of figures or word problems lets the young idea choose the appropriate expression between "a x b" and "b x a". The following picture makes clear the distinction between the multiplicand and the multiplier, or between the equal number of objects in each group and the number of groups [Inada 2011].

In cooperation with reciting the kuku table to find the product quickly, the pupils meet and solve a variety of problems [Tsukuba 2003]. We refer to the word problem seen in the Introduction as the apple problem and will also name other word problems after the object in it. The apple problem is classic in the sense that the multiplicand occurs later than the multiplier. This sort of problem has been on the test, not only in term-end exams but in achievement tests which cover several schools in one or more municipality [Shimizu 2011].

Teachers expect that the apple problem corresponds to the following diagram for example.

When the marker who is usually the teacher has a glance at the math sentence "5 x 3 = 15" in response to the apple problem, therefore, he or she supposes that the pupil does not understand the meaning of multiplication to cross the answer in red. The left-hand side, "5 x 3", opens up the eyes of the marker so that the answerer made the multiplicative sentence by sequencing the numbers in order of those in the question and connected them with the symbol "x". Although there is so strong criticism against it and the well-known contentions are discussed below, I point out right now that this way of recognition and judgment has been shared among the people engaged in the elementary math education. Plenty of experts have indicated the significance of the distinction between the multiplicand and the multiplier when making a multiplicative sentence. Some of them aggressively recommend the word problems like the apple problem for the purpose of inducing the separation.

The pupils in the third grade learn the division using the knowledge of the multiplication. The elementary math education requires them to write an appropriate math sentence for the situation involving zeros, decimals and fractions for the last time. The effort is also known as the "choice of operation".

A class is sometimes a place where all the pupils take themselves the task of a common problem. This is closely related to the problem-solving activity. The teacher has to prepare the coursework carefully, including a list of the math sentences that the pupils are likely to give as the answer. More than one math sentence is often correct. In the class, actually, the pupils write (or the teacher presents) candidate answers on the blackboard and compare them in terms of the correctness and the application potentiality to yield the knowledge. It is OK for the pupils to make a mistake at that point, and the teacher plans the class supposing and welcoming their failure and confusion. The well-organized class allows the pupils to work out a solution of the untried situation.

The learning environment like this indicates a striking contrast to that in U.S. where teachers attempt not to spawn errors by demonstrating the solution and then letting their pupils apply to similar problems. Stigler and Hiebert [Stigler 1999] offered much praise to the Japanese-style math education which includes the problem-solving activity together with "jugyou kenkyuu" (lesson study).

3. Dealing-out

Let us get back to the apple problem. For that problem, we can take the following procedure:

  1. Lay out 5 dishes and make 15 or more apples ready.
  2. Put an apple on each dish, saying "first round".
  3. Hand out apples in the same manner, saying "second round" and "third round".

After finishing the procedure, you can see 5 dishes and 3 apples on each dish!

We can understand this procedure through the operation for dealing cards. The way of arranging the objects given above is therefore called "dealing-out". It was Toyama Hiraku, an educator as well as a mathematician, that wrote an article in 1972 which applies the dealing-out to the multiplication situation [Toyama 1972].

The dealing-out swaps the roles of multiplicand and multiplier. In the above procedure, the number of objects in each group is "5 apples", which equals to the number of each distribution at a time. On the other hand, the number of groups is "3 times". Finally "5 x 3 = 15" gives the math sentence. Attaching the units (spelled singularly) to the quantities, we can write "5 apple/time x 3 time = 15 apple" whereas the original apple problem corresponds to "3 apple/dish x 5 dish = 15 apple".

4. Product-based Problem and Product-oriented Solution

Toyama provided the following two word problems in his article.

  • "You have to give 6 children 4 oranges respectively. How many oranges can you have altogether?"
  • "There are 6 desks in a row and 4 such rows in the classroom. How many desks are there altogether?"

More precisely, he presented the desk problem for asserting that both "6 x 4 = 24" and "4 x 6 = 24" should be correct math sentences.

Applying his point of view to the apple problem, we can illustrate the following array diagram.

As you can see, there are no encirclements and the dots are not grouped. If we had to describe the math sentence looking at this picture, then "3 x 5 = 15" and "5 x 3 = 15" should be right. Actually the problem collections including this type of question are available at bookstores, although Japanese math education has not paid any notice to the dealing-out in multiplication.

Let us name the set of these problems together with the cognitive model. We refer to the problem that shows the situation of multiplication with no distinction between two factors as a "product-based problem". In addition, the way of thinking of the multiplication situation as the one with no distinction between a multiplicand and a multiplier is called the "product-oriented solution".

Among integers, we can transform any multiplication problem into an array diagram in principle. Cartesian product generalizes the targets. Replacing dots with squares and sticking them together, we have the rectangle. Then the calculation of the area of rectangles belongs to a product-based activity, whether the lengths are represented as integers, decimals or fractions. Derivation or computation of physical quantities such as momentum and electrical energy is also based on a product-based situation.

5. Multiple-based Problem and Multiple-oriented Solution

We define another sort of problem of multiplication together with its cognitive model. The problem presenting the situation of multiplication which distinguishes the multiplier from the multiplicand is a "multiple-based problem", while the way of interpreting the multiplication situation as the one with such a distinction is called the "multiple-oriented solution".

The commentaries of the Education Ministry guidelines [CEMG 2008] about mathematics introduce the multiplication by means of "calculating the amplitude of the several number of a fixed quantity". I think that this is the basic multiple-based situation. The apple problem is obviously multiple-based. Beyond integers, multiple-based problems include (1) the total amount of juice where the equal quantity is distributed to several persons, (2) the distance with the speed and the amount of time given, and (3) the proportional situation.

The multiple-based mathematical investigations are available. Takagi Teiji [Takagi 2008] derived the real numbers as the ratio of two quantities in a quantity space, according to his argumentation written in the beginning of the 20th century. Many decades passed and Nagumo Mitio [Nagumo 1977] defined the automorphism (the linear mapping) of a positive system of quantities to identify a mapping as a multiplying factor which may be a real number. Tamura Jiro [Tamura 1978] succeeded to Nagumo's work and investigated the quantity such as an area or a velocity that is drawn from two quantities. The book of linear algebra by Kojima Jun [Kojima 1976], which associated a linear mapping between disparate two quantities with a quantity taking a velocity or a density for instance, is listed in the reference of Tamura's one.

6. Which will it be?

In advance of the comparison between the two paradigms for multiplication, I would like to give a couple of information supplements. Firstly, there were attempts to classify the situations to which the multiplication is applied. For example, Greer [Greer 1992] broadly divided the situation of multiplication into "the context where the multiplicand and the multiplier are distinguished" and "the context where there is no distinction between a multiplicand and a multiplier". These contexts are compatible with the multiple-based and the product-based situations. Moreover he made a classification to attach the example problem to every representative situation. His classification table has seven multiple-based situations and three product-based situations. It is interesting that there is a figure of the dealing-out in it for providing an example of the partitive division.

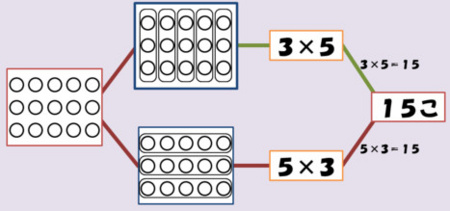
Alternatively we can understand two thinking processes through a series of figures. Before the way of solving the apple problem with the multiple-oriented solution, I am obliged to show a wider circumstance, or the perspective. (What is just after "15" on the rightmost box is a Japanese character meaning "piece(s)", because these figures were originally prepared for Japanese readers of my blog.)

When we start with the leftmost array diagram, there are two ways of assigning the pair of "the number of objects in each group" and "the number of groups", namely the second array diagrams up and down from the left. That is why two math sentences are valid in this case. However the reaction to the apple problem is localized on the figure, as follows.

In other words, the upper array diagram second from the left must be the source in the perspective and the only one multiplicative sentence is accepted.

From the viewpoint of the product-oriented solution, the following figure is the simplest total image.

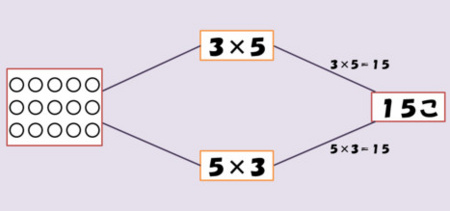
And then, the leftmost array diagram is associated with the first-stage graphic for the apple problem. Another figure can be drawn for the product-oriented solution, where the source is the same as with the multiple-oriented one, and the red and the green lines show the paths to lead to the amount with different ways.

Then, are the multiple-based and the product-based situations incompatible, like oil and water? I do not think so. In fact, we can reduce the multiple-based situation or problem to the product-based one, and vice versa.

Look at the following figure to understand the reciprocal conversion for the multiplication of integers.

By eliminating the encirclement, we can have the natural array diagram, or the product-based situation. Conversely, given an array diagram without enclosures, we can assign the number of dots in each group together with the number of groups. In this case, there are at least two ways which lead to the different math sentences; both "a x b" and "b x a" are accepted as the expression of the situation.

As decimals and fractions are concerned, the notion of compound proportion (n-linear function in [Vergnaud 1983]) plays an important role in the product-based situations. For example, "Iron is 0.88 times as heavy as copper. If a piece of copper weights 4.2 kg, how much does a piece of iron the same size weigh?" [Greer 1992] seems nothing but a multiple-based problem where 0.88 is the multiplier. However, the question can be generalized into "Iron is P times as heavy as copper. If a piece of copper weights Q kg, how much does a piece of iron the same size weigh?" Since the weight R is proportional to both P and Q through the product-oriented solution, "R = P x Q" and "R = Q x P" are derived. I might as well mention the fact that the multiple-oriented approach is ready for any compound proportion by interpreting the situation as the separate proportions.

The above discussion follows that the multiple-oriented and the product-oriented solutions are equal in a mathematical or logical sense. To put it another way, we cannot say that one excels in the other.

And then, which is adopted in education at schools? As far as the documents in Japan and abroad I have read, I have no other choice but the multiple-oriented solution. Word problems in the second grade are basically multiple-based. Indeed product-based ones can be seen, but they are not introductory situations. Moreover, pupils are expected to solve a question like this through the multiple-oriented solution; some find the number of objects in each group and the number of groups; some calculate the amount by repeated addition.

An intriguing episode outside Japan was reported [Tsubota 2010]. A pupil wrote the math sentence for the 6 spots of a dice before others said it was wrong one after another. The Japanese educator released it as an experience in Brazil, where the child appropriately recognized 3 spots in 2 groups respectively but switched the multiplicand and the multiplier when writing the math sentence up on the blackboard. Although it is not always on the test abroad, the distinction between the multiplier and the multiplicand is under pupils' senses.

The product-oriented instructions are seen in France [Vergnaud 1983] and in China [Kokkyoken 2009][Takahashi 2011]. The issues were pointed out at the same time with regard to the understanding of the learners and an application to the quantity involving proportion at the same time.

7. To Support the Understanding of "Number of Objects in Each Group"

In this section the target is restricted so that the factors may be positive integers. The ability of finding the number of objects in group and the number of groups from situations of the multiplication would be useful to subsequent study or to daily life. I am convinced that the ability is effective in arrangement of quantities. For example, making the scoresheet of a darts-like game is not only delightful but significant in the educational sense. In addition, the case in which the quantity of each group is fixed but the number of groups varies is much more frequent than the reversed case. It is true that magnification and proportion tend to keep the multiplier immobile, but those cases should be concerned with the mapping or the calculation among decimals, fractions and real numbers.

To enhance such capabilities might be feasible in the first and the second grades. In fact, the Education Ministry guidelines make mention of "skip counting" in the first grade. The initial actions are saying "2, 4, 6, 8, 10, ..." and "5, 10, 15, ...", namely the numbers every two and five. By counting up the objects, we can easily know the fixed number in each group, the number of groups and the amount. This implies that children can know the primitive form of the multiplicand and the multiplier, far ahead of the multiplication.

To know an actual case of learning the skip counting, [Maekawa 2011] is worth reading. Since it was intended for elementary school teachers, the book consists of the proposals of educational guidance. But anyone can buy and read it to get a grasp of the key points in the class. The word problem on page 66 is "There are 3 children. You will give 2 oranges each. How many oranges do you have altogether?", and I would like to emphasize that this is not for the multiplication but for skip counting. Remarkably, the note of instruction reads "Let the pupils focus attention on the distributed situation, but not on how to distribute the oranges." This way of understanding the situation attempts to overcome the dealing-out. A large number of publications and proposals of educational guidance agree with this policy.

Another book can accelerate the understanding and learning of the foundation of multiplication. [Tanaka 2010] is a problem collection by Tanaka Hirosi, who is an elementary school teacher and influential to Japanese math instruction with his many publications and collaborative works. When solving the questions in the book, one learns to tie up the word problem, the figure and the math sentence of a situation.

The instruction can be realized in education in the home as well. All you have to do is keep the children paying attention to the result but not to how to distribute the objects. Through the problems, in some of which the number of objects in each group (the multiplicand) precedes and in some of which the number of groups (the multiplier) appears in first, the children will take their own learning to a higher level. After finishing the book, anyone can recognize the multiplicand and the multiplier in a given word problem, with a rich image of the situation!

8. Order-of-multiplication Dispute

The instruction of multiplication motioned above has been controversial in Japan, which is called the "order-of-multiplication" dispute. There are people who are mostly outside elementary schools and remedy the way of instruction that interprets "3 x 5" as one and only one correct answer to the apple problem and puts a cross in a red pen on "5 x 3". In 2011, a book in the opinion of the nonsense of such a teaching was published [Takahashi 2011].

We can see various reasons on the net why the multiplication instruction at present is inappropriate. A list of representative arguments, except the dealing-out and the product-oriented solution, together with my comments is as follows:

  • "If the multiplication is identified, then we do not need the distinction between a multiplicand and a multiplier." --- The identification is much harder than you think because the choice of operation is a well-known issue in math education. Even limited to the multiplication, the way of recognition like that would disable children to choose two factors accurately in an infoglut situation, say "You are going to buy 4 bottles. Each bottle contains 280mL of juice and costs you 136 JPY (Japanese yen). How much do you have to pay?"
  • "The multiplication is subject to the commutative law." --- The commutative law is available in calculation but not in validation of the operation. The application of the commutativity to the apple problem would conduce to the following figure, which fails to combine the situation with the math sentence.

  • "In other countries, the multiplier is on the left. We write '4 x 100m' but not '100m x 4' for a medley relay, don't we?" --- Examples both domestic and overseas lead to an outline of the studying environment in common; the classroom allows the pupils to make a mistake. The teacher reminds them of their learnings while they bring what they answered into check to think or say "I get it!" This process leaves little room for foreign, unshared knowledge.
  • "In other countries, the right and left numbers of the multiplicative sentence do not matter and the order is out of marking." --- As shown by the dice problem in Brazil, children are aware of the distinction of two factors. Differently I would like you to disclose your opinion of how and what the pupils acquire through the learning of multiplication. My understanding is open in the previous comment.
  • "There should be permitted more than one way of solving a problem." --- Yes, the class typically encourages the pupils to produce various answers based on diverse ways. And one of them (or more) is what they will share, the teacher wishes, in the class and some of them are correct in a mathematical sense but less interesting, and some are the answers or approaches which the children will see as wrong. I found sophisticated problems to prevent the deal-out and make it impractical. If you applied it to the word problem "There are 3 boats and 2 persons are on each boat. How many persons are there altogether?", then the boat taking on only one person would be unstable and he or she would feel lonely.

I would like to share with you the fact that all those reasons came from the adults, apart from the studying pupils. The originators do not seem familiar with the past and current elementary education of mathematics ranging from the methods of teaching to the field surveys of comprehension.

The criticisms are persistent on the net, though, there are few people engaged in elementary math education who approve of the opinions. To the best of my knowledge, neither the research papers discussing the "order-of-multiplication" nor the scientific research funds to this subject are found.

9. Conclusions

In this article I have presented the grounds for making the math sentence "5 x 3 = 15" valid or invalid in response to the apple problem where "3 x 5 = 15" is supposed to be correct. Due to the discussion between multiple-oriented and product-oriented solutions, and due to the literature search of the math instructions in Japan and overseas, I do approve of the classes in which the pupils make sure that "5 x 3 = 15" is not appropriately described for the apple problem.

I believe that the education is an iteration of propositions and choices. Not only in policymaking of the education platform that has an impact on all the country but in the meeting of a school for "jugyou kenkyuu", someone makes a suggestion in accord with conventional knowledge and implemented methods. Whether it is accepted or not seems to be dependent at least on consistency of the relevant learnings. Since the pupils have learned the skip counting and done the exercises to recognize the situations, the distinction of the multiplicand from the multiplier is educationally valid and effective.

If the readers nevertheless would like to accept "5 x 3 = 15" as another correct answer to the apple problem within the framework of the math education, then we would have to achieve the results of the pupils' comprehension of operations, numbers and quantities and/or their problem-solving ability by means of qualitative studies and quantitative valuations, continuing the discussions about the educational, mathematical and practical significance. When the time comes I will receive with joy the picture which brings the enrichment of mathematics to pupils, teachers and all the people.

References

About the Author

"takehikom" is a college teacher who is engaged in computer and communication engineering. Not involved with elementary schools directly, he has collected the study guides and professional literature written for the understanding of the multiplication, and evidenced his approval to the present instruction by adding an engineering approach. There were a large number of blog articles in Japanese about this topic while he has written in the blog the articles of child-raising and the introductions of his own Ruby scripts that deal with the arithmetic operations and "kuku" word problems. His research area includes the expression of information, which was actually of use to make a drawing of the thinking processes of a situation. He has also talked about the essence in his class of programming or information security as an aside.
This article is his first attempt written in English, intended to present Japanese-style instruction of multiplication in the elementary education to the world in his own way. When redistributing this material offline, please e-mail takehikoATsysDOTwakayamaHYPHENuDOTacDOTjp.