優しい本

かけ算の意味について，新書で「優しく」書かれている本を読みました．

算数再入門―わかる、たのしい、おもしろい (中公新書)

9 掛け算について

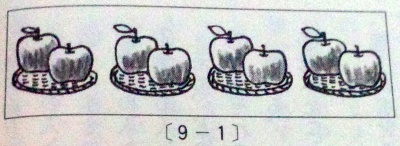
「左の絵にはリンゴがいくつありますか?」と問えば、8個という答はすぐに返ってくると思われます。しかし、このリンゴの数え方にはいろいろあるでしょう。「1、2、3、4……」と1つずつ順に8まで数える人もいれば、「2、4、6、8」と2個ずつ数える数え方をする人もいることでしょう。
この「2個ずつ4つある」という考えが、掛け算の素地と言えます。
私たちの身の周りには、同じ数ずつあるものがたくさんあります。6個パックに入った卵、12本ずつ箱に入った鉛筆など、すこし探せば同じずつまとまっているものがすぐに発見できるでしょう。その総和を求めるときに、「何個のいくつ分」ととらえるから、掛け算の思考が始まります。掛け算を教えるときは、「2＋2＋2＋2」というように、同数累加（同じ数ずつ足すこと）から始まり、「2個ずつの4個分」という考えを理解した上で、「（1つ分の大きさ）×（いくつ分）＝（全体の大きさ）」という掛け算（乗法）の意味を表した「言葉の式」として一般化した式で考えるようになります。この式はやがて「（基準量）×（割合）＝（割合にあたる量）」へと発展し、中学校では、多項式の項である単項式の意味になります。例えばという二次方程式も多項式ですが、この多項式の項であるを表すやを表すや単独の文字や数字のはすべて単項式となります。
また、「倍」という関係を表す言葉も、日常的に使われています。「倍」とは「ある量を基準とする大きさで測ったとき、基準とする大きさのどれくらいに当たるか」を表しています。図のリンゴ8個は、2個ひとまとまりのリンゴの4倍です。つまり、「倍」は、基準とする大きさを1としたとき、ある量が基準のいくつ分に当たるかという、割合の1つの表現と見ることができます。
(pp.40-41)

「優しい」と感じたのには，大きく2つの理由があります．
一つは，押しつけでないということです．他のかけ算の考え方や教え方を，排除していないわけです．
もう一つは，小学校1年生から大人までで，かけ算と関わる場面とその経過・発展が目に浮かぶ点です．「雄大」と言ってもいいかもしれません．
1年からのかけ算，とは，「掛け算の素地」のことです．“2ずつ”などの「まとめて数える」活動は，1年から入っていますし，米国のCommon Core State Standards for Mathematicsにも，"Work with equal groups of objects to gain foundations for multiplication."が2年に書かれています（乗除算は3年です）．"foundation"が，「素地」の英語表現としてぴったりです．

先日入手した本に移ります．

数とは何か?―1、2、3から無限まで、数を考える13章 (BERET SCIENCE)

どのお皿にもミカンが3個のっています。お皿は全部で4皿あります。ミカンを集めて大きな袋に入れると、全部でいくつになるか?

これを次のように表す。
3個/皿×4皿＝12個
あるいは、
4皿×3個/皿＝12個
(略)
少しやさしい言葉でいえば、
（1当たり量）×（いくつ分）＝（全体量）
または、
（いくつ分）×（1当たり量）＝（全体量）
となる。
(pp.42-44)

ふむ，一つの場面に2つの式ですか．「やさしい」ですか．ともあれ読み進めます．

■ かけ算の順序
「どのお皿にもミカンが3個のっています。お皿は全部で4皿あります。ミカンを集めて大きな袋に入れると、全部でいくつになるか?」という問題の答えを
3個/皿×4皿＝12個
という順序で表さなくてはいけない、と思い込んでいる人が多い。
4×3＝12　だから、12個
とか、
4皿×3個/皿＝12個
と書くと間違っていると思う人がいるというのだから困ったものである。
1皿当たり3個のミカンがのっていて、そのような皿が4皿あるのだから、4皿×3個/皿＝12個と考えるのは自然な発想なのである。この自然な、ある意味では合理的な思考を無理にやめさせようという考えは無理が生じるのである。
「かけ算の順序」について、「（1当たり量）×（いくつ分）」にしなければならないかを、子どもたちにいかに教えたかという小学校教師の奮闘記が新聞で紹介されたことがあるが、そんな先生の苦労を解放してやらなければならない。
「意味のないこと」「無駄なこと」「間違ったこと」を一生懸命教える先生がいなくなることを願うばかりである。
(pp.46-47)

この一節は，「優しい」と正反対の位置にあります．
言葉を拾うと，「と思い込んでいる人が多い」「小学校教師の奮闘記が」「一生懸命教える先生が」と，“人”が何度か出てきます．
しかしそれらの“人”は，その認識や行いを改めるべき対象として書かれています．もちろん著者の外の存在です．『算数再入門』の引用では，「私たち」が1箇所で，全体として，著者と読み手が認識をシェアできるように書かれているのと，対照的です．
さて…その記述に該当する“人”が，上記引用やその前後を読んで，「そうか，かけ算ってこう考えればいいんだ，よし改めよう」と思うのかというと，難しそうです．小学校の先生方はおそらく，「4皿×3個/皿＝12個」のタイプの表現を，教科書や書籍からも，日常生活からも，見つけることができないのです．
参考文献がないこと，「かけ算の順序」という言葉が定義なく出現していることから，上の引用で「そうだそうだ」と思う人々---想定する読者---はあるわけです．小学校の先生方とは，氷炭相容れずなのかなあとも思います．
「思います」ばかりも好きではないので，テクニカルな話を2点．

• 「どのお皿にもミカンが3個のっています．お皿は全部で4皿あります．ミカンを集めて大きな袋に入れると，全部でいくつになるか?」

と

• 「お皿は全部で4皿あります．どのお皿にもミカンが3個のっています．ミカンを集めて大きな袋に入れると，全部でいくつになるか?」

とで，かけ算を学習した子どもたちが書く式の割合（「3×4」に何%，「4×3」に何%，など）は異なります．そのものずばりの実験をしなくても，学力調査・学術調査から，推論できます．
字数の都合もあるのでしょうが，かけ算の構造だとか，子どもたちの認識だとかの部分が，おろそかになってしまったのは，残念なところです．
「小学校教師の奮闘記」はasahi.com（朝日新聞社）：２×８ならタコ２本足 - 花まる先生公開授業 - 教育と思われます．しかしそこには，「かけ算の順序」も「1当たり量」も出てきません．そしてあの記事から学ぶべき最も大事なことは，順番を逆にして書くと意味が変わっちゃう（変わり得る）という事例です．

本ではないのですが，「優しい」方に質問をする機会がありました．
今月某日，座長を務めた件の，最後のご発表です．日本舞踊の研究はほとんど知らないけれど，CHやじんもんこんで，それなりの頻度，発表されているのは，知識として持っていました．事前に発表者をWebで検索し，名前の読み方などをチェックしていたところ，今回の発表者が高名な教授であることを知りました．
質疑の時間に，超過を承知で（座長!），尋ねました．デモされていた動画を見て所作の良し悪しが分かる“デジタル”な人も，それではなく人の動きで分かる“アナログ”な人も，日本舞踊をしている人にはいそうで，先生は，アナログ・デジタルの両方が分かる方なのではないか，といったことを含め，当を得ない質問内容になってしまいました．
回答は，発表と同様の柔らかい語り口の中に，踊りの稽古のご苦労を入れながら，お話をされていました．3分ほどオーバーしてしまいましたが，得がたい経験をしました．

関連：

• 優しいが易しくない本
• 『数とは何か？』小林道正
• 小学2年生の乗法場面に関する理解
• かけ算の順序で数教協とナマ議論（3回目／4回） | メタメタの日：「先ず，小林委員長の本については，そもそもそういう本が出たことを知らないようだった。」