わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

チャート，リスト，分類

OoM

かけ算の順序論争が長期間に及ぶと，意見や論点を整理したいという要望が発生します．そして実際，いろいろな論点整理をWeb上で読むことができます．本日は，その集約を試みました．

チャート（ツリー，樹形図）

リスト（箇条書き，付番号）

反論のための反論の列挙の列挙からの転載です．

この問題に対しては，さまざまな観点からの批判が混在しているようです．
　
　例えば，曰く
(1) どんな考えでこのような指導を行っているのか？
(2) テストで×とするのはどうなのか？　その後のフォローはどうなっているのか？
(3) 指導者や学校によって指導の仕方が異なるのは問題でないのか？
(4) 欧米とは指導が異なっているので，外国籍の子や帰国子女の子には馴染まない指導である．
(5) 知的に高い子どもには，早くから次の段階を教えるべきなのではないか？　違う教え方の方が合っているのではないか？
(6) そもそも，“具体物のまとまりをかけられる数とする”という指導は，子どもにとって本当に望ましい指導なのか？
　…などなど．

pha11.info

さて、少し情報を集めているうちに、順序にこだわる人達の中にも、色々な人が居るらしい事が解ってきた。概ね、以下の様に分けられると思う。
1)順序にこだわるのが「数学的にも正しい」と信じている人
2)学習指導要領に書いてあるから（いや、本当は書いてない事を読み取っているだけなのだが）その通りに教えるべきだと考える人
3)子供の発達段階に応じた理解をさせる為の便法（もっと言えば、必要悪）であると考えている人
4)子供に理不尽な事や「正しくてもバツを貰う」経験をさせる事も必要であると考える人、あるいは「子供は教師の言った事をそのまま覚えるのが正しい、疑問など持たずに鵜呑みにするのが正しい」と考えている人
などである。

PseuDoctorの科学とニセ科学、それと趣味: 掛け算の順序論争について

「かけ算の順序」に拘る教え方を擁護する意見は少なくない。またその理由も様々であるが、大ざっぱには以下のよう３つに分類できる。
Ａ　（１つあたり）×（いくつ分）というルールになっている。そのように教えることになっている。
Ｂ　算数の教え方として、その方が優れている。
Ｃ　教師は一生懸命やっているのだから、とやかく言うべきでない。
Ｃ’理不尽なことを経験させるのも教育。教師が間違っていることもあるという社会勉強になる。

「かけ算の順序」擁護論の概略 算数「かけ算の順序」を中心に数学教育を考える/ウェブリブログ

3×5を正解とし、5×3を訂正させたことを問題視する議論は、次のように分けられる。
(1) 訂正させるのは良いが、モデルが明確にされていないことへの批判
(2) 数は量の抽象論「ひとつあたり×いくつ分」のモデルに従わせることへの批判
(3) 前提とするモデルを認めても、どの問題にもひと通りの立式しか可能でないという思い込みへの批判
(4) 特定のモデルに従わせることへの批判
(5) 「5×3」と「3×5」を区別しようとする態度への批判、
（https://sites.google.com/site/orderofproduct/endoff．デッドリンク）

俺流分類

  • A-1: かけられる数とかける数は交換可能である．乗法の交換法則により，5×3＝3×5が成り立つ．
  • A-2: トランプ配りをすれば，かけられる数とかける数を交換できる．上の問題だと，「5個ずつ3回」になる．
  • A-3: りんごを長方形に配置すれば，その総数は5×3で表すことができる．
  • A-4: 皿の枚数をかけられる数，1皿あたりのりんごの数をかける数と見なせばよい．
  • A-5: 単位を付けて書くと，「5×3個」と「3個×5」，「5枚×3個/枚」と「3個/枚×5枚」は，それぞれ同じである．
  • A-6: 他の国では，式で表したとき，かけられる数とかける数の位置が反対になる，もしくは，どちらでもよい．
  • B-1: この問題では，1皿あたりのりんごの数がかけられる数であり，皿の枚数がかける数となる．
  • B-2: 5×3と3×5は，かけ算の答えは同じでも，意味は異なる．
  • B-3: 5×3＝15の式では，皿の数とりんごの数が反対である．
  • B-4: 5×3＝15の式では，積は皿の枚数になってしまう．
  • B-5: 単位を付けて書くと，「5個×3」と「3個×5」，「5個/枚×3枚」と「3個/枚×5枚」は，それぞれ異なる．
  • B-6: 言語や文化の違いに配慮しながら式で表すことが教育上有益である．
かけ算の順序論争について（日本語版）
  • 被乗数と乗数が区別され，「b×a」と書くと，「a×b」とは式の意味が異なるとされるかけ算を，《倍の乗法》と呼びます．
  • 被乗数と乗数の区別は本質的ではなく，「b×a」と書いても，「a×b」と同じ場面や対象を表していると解釈できるようなかけ算を，《積の乗法》と呼びます．
  • 《倍の乗法》に基づいて，乗法を意味づけるべきだという考え方を，《倍指向》と呼びます．
  • 《積の乗法》に基づいて，乗法を意味づけるべきだという考え方を，《積指向》と呼びます．
  • 《倍指向》とは，かけ算で表すことのできるどんな場面や対象も，《倍の乗法》に帰着できるという考え方のことです．
  • 《積指向》とは，かけ算で表すことのできるどんな場面や対象も，《積の乗法》に帰着できるという考え方のことです．
倍指向と積指向の整理

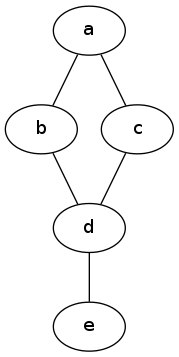
簡潔に表すなら，「束(lattice)」かなと思います．図にするとこう．

各文字の意味は次のとおりです．

  • a ≡ 後述のbの求め方で得られる「３×５」，cの求め方で得られる「５×３」を比較し，cの書き方だとdと誤解される可能性を考慮してbの求め方を採用し，「しき」に「３×５＝１５」と書く．
  • b ≡ 問題文から，「１つ分の大きさ」が（1皿あたり）3個，「いくつ分」が5枚であるのを読み取り，「しき」に「３×５＝１５」と書く．
  • c ≡ 問題文から，皿に順にりんごを配ること*1をイメージし，「１つ分の大きさ」が（1回で配る）5個，「いくつ分」が3回であると解釈し，「しき」に「５×３＝１５」と書く．
  • d ≡ 問題文から，かけ算で計算できる問題だと認識し，問題文に現れる数字のうち５と３を順に取り出して，「しき」に「５×３＝１５」と書く．
  • e ≡ その他の誤答（白紙，数字の書き間違いなど）
分かりやすく抽象的に・2010年11月バージョン

図表も箇条書きもありませんが，「かけ算の順序」のダブスタ考もまた，分類の事例となっています*2．

思ったこと

- 「掛け算順序固定」問題対策本部 - アットウィキは，2012年初頭に私自身が驚きを覚えたことの一つでした．というのも，ある時点での大幅改訂により，造語である「倍指向」「積指向」が取り入れられたのでした．そして編集者による解釈も，チャートの作成目的あるいは当該Wikiにおける文脈のもとで，当を得た記述となっています．
さて，本記事で集約を図った「チャート」「リスト」「（俺流）分類」を見ていると，気になる点があります．チャートとリストは，論点あるいは論者を振り分けるための道具とすることができます．それに対し俺流分類は，主要な項目にラベルをつけた上で，項目間の関係を明らかにしようという意図を持っています．
別の言い方をするなら，チャートとリストは，ともにツリー構造です*3．それに対し俺流分類はいずれも，グラフ構造となっています．
それらに優劣をつけることはできません．ともあれ，スタンダードな方法をとらないでいると，文字数を多くして説明しなければならないことを，教訓にするとしましょう．

*1:誤解されず，かつ最も簡潔にこの操作を記述するにはどうすればいいか，思案中…．

*2:各行を「式の読み取り方」，各列を具体的な式（2×5，5×2）として，表形式にするのが良さそうです．後で述べるツリー構造・グラフ構造との対比で言うと，マトリックス構造になります．

*3:各リストは，一つの親と複数の子からなる，深さ2の有向木と見ることができます．