わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

かけ算の順序論争について（日本語版）

OoM

目次

  • 1. はじめに
  • 2. 正解・不正解の理由
    • 2.1 正解とする6つの理由
    • 2.2 不正解とする6つの理由
    • 2.3 各理由の賛否
  • 3. かけ算をめぐる状況
    • 3.1 かける数が先の文章題
    • 3.2 a×bとb×a
    • 3.3 「倍」と「積」のかけ算
  • 4. 日本の算数教育の特徴
  • 5. おわりに
  • 参考文献

改訂履歴等はhttps://github.com/takehiko/oomdocをご覧ください．

1. はじめに

小学校の算数で，2年で学習する重要な事項といえば，「かけ算」である．かけ算の式で表すことを学ぶとともに，九九を暗記する．現在では，4×12のような九九の範囲を超える式も，2年で学習している[Link 1J][文部科学省2008]．筆算は使用しない．例えば，九九による4×9＝36と，「かける数が1増えれば積はかけられる数だけ増える」という性質により，4×10＝40，4×11＝44，そして4×12＝48を得る．もしくは，交換法則と累加から，4×12＝12×4＝12＋12＋12＋12＝48とすることもできる．

テストでは，次のような問題が見られる（「りんごの問題」と呼ぶ）．

「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」という出題と，「しき」と「こたえ」を書く欄からなる．児童は「しき」に「5×3＝15」，「こたえ」に「15こ」と書いた．すると「こたえ」はマル印がついて正解だが，「しき」がバツ印で不正解となっている．そしてこの問題の正解となる式「3×5＝15」が，赤ペンで書き加えられている．問題文では5が先，3が後に出現しているが，学習した「かけ算の意味」をもとに，2つの数をひっくり返して「3×5」と書かないといけない，というのが「かけ算の順序」の基本的な考え方である．

これに対し，さまざまな理由で，「5×3＝15」も正解とすべきだという主張がなされている．インターネット上のみならず，『かけ算には順序があるのか』[高橋2011]をはじめ書籍でも，取り上げられた．2013年10月，韓国でも議論があり[Link 2K]，その中で筆者の英語記事[Link 3Et]がリンクされた．筆者は韓国語が分からないが，いくつかのコメントを機械翻訳にかけてその意図を知り，そこから，かけ算の論争を世界レベルで共有すべきではないかと痛感した．

そこでこの文書では，「かけ算の順序」あるいは「かけ算の意味」について，情報の整備を試みた．日本の算数・数学教育の一面について，海外の関心ある人々が読めるようにしている．後でも述べるが，筆者は上の答案について，不正解とすることに賛成の立場である．
本論に入る前に，日本の教育の前提をいくつか挙げておく．かけ算は「かけられる数×かける数＝かけ算の答え」の式で表される．赤のマルが正解，バツが不正解というのは，世界共通ではない．年度は4月に始まり翌年3月に終わる．

2. 正解・不正解の理由

2.1 正解とする6つの理由

「5×3＝15」を正解とする理由について，インターネット上の情報や書籍で読んできた中から主要なものを選び，以下の6項目からなるリストを作成した．

  • A-1: かけられる数とかける数は交換可能である．乗法の交換法則により，5×3＝3×5が成り立つ．
  • A-2: トランプ配りをすれば，かけられる数とかける数を交換できる．上の問題だと，「5個ずつ3回」になる．
  • A-3: りんごを長方形に配置すれば，その総数は5×3で表すことができる．
  • A-4: 皿の枚数をかけられる数，1皿あたりのりんごの数をかける数と見なせばよい．
  • A-5: 単位を付けて書くと，「5×3個」と「3個×5」，「5枚×3個/枚」と「3個/枚×5枚」は，それぞれ同じである．
  • A-6: 他の国では，式で表したとき，かけられる数とかける数の位置が反対になる，もしくは，どちらでもよい．

以下の画像は，トランプ配りをすれば「5×3＝15」になることを示したGIFアニメーションである．

A-2およびA-4は，「かけられる数×かける数」でかけ算の式を表すという算数のルールの下でも，5×3が正しい式であるという理由を示している．それに対し，A-5およびA-6は，「かける数×かけられる数」も，適切なかけ算の式であるという主張となる．
A-5に書いた「単位」について，Wikipedia日本版では「助数詞」[Link 4J]で詳しく解説されている．英語版には"Japanese counter word" [Link 5E]がある．また単位付きの式は，算数の教科書には見当たらない．しかしこれは日本固有というわけではなく，[Schwartz 1988]に記されている"referent"が相当しており，国外の数学教育の研究にも事例が見られる．さらに言うと，「/ (per)」を用いた分離量の単位表記は1970年ごろ発生したものである（「/」を積極的に推進している数学教育協議会の著作物で，1961年と1971年に発行された『水道方式入門』[遠山1961][遠山1971]を読み比べるとよい）．

2.2 不正解とする6つの理由

「5×3＝15」を不正解とする理由についても，主要なものを選んでリストにした．

  • B-1: この問題では，1皿あたりのりんごの数がかけられる数であり，皿の枚数がかける数となる．
  • B-2: 5×3と3×5は，かけ算の答えは同じでも，意味は異なる．
  • B-3: 5×3＝15の式では，皿の数とりんごの数が反対である．
  • B-4: 5×3＝15の式では，積は皿の枚数になってしまう．
  • B-5: 単位を付けて書くと，「5個×3」と「3個×5」，「5個/枚×3枚」と「3個/枚×5枚」は，それぞれ異なる．
  • B-6: 言語や文化の違いに配慮しながら式で表すことが教育上有益である．

B-3およびB-4が絵になった授業例がある[筑波2003]．


「自動車が5台あります。タイヤの数はいくつでしょうか」という問題で，「1台にタイヤは4本」というヒントを得て，4×5＝20と書く．ここでもし，「5×4」だったら，5つのタイヤがついて「五輪車が4台」となる図や，家に車が入った「5台ずつが4つ」という図によって，問題に合っていないことが視覚化されている．

2.3 各理由の賛否

リストを作ることで，それぞれに対する賛否を明確にしやすくなる．筆者はというと，A-1からA-6までのいずれにも賛同できない．問題文を読み，かけ算で求められると判断すること，すなわち演算決定は，交換法則の適用(A-1)よりも前に行わなければならない．

式に対する解釈の多様性は，A-2だけでなくB-3およびB-4も考慮する必要がある．りんごの問題で「5×3」と書いたら，A-2，B-3，B-4の解釈が可能であるのに対し，「3×5」と書けば，これまで学習してきたかけ算の意味に基づくと，そういった解釈の余地がない．なので誤解のより少ない式を選ぼう，という考え方である．2つの式を比較し選択することは，かけ算の意味を学ぶ際の学習指導案にもよく記載されている．
またトランプ配りは現在，等分除の操作として用いられている[Anghileri 1988][水戸部2012]．配る操作をする際，総数が決まっているからである．それに対し，「a人にb個のりんごを配りたい」という場面では，配る操作をすることなく，総数をかけ算で求めることになる（配る操作と加減乗除との関わりについては[文部省1986]が詳しい）．総数が未知で，トランプ配りの操作を考慮した学習指導案もあるが[前川2011]，「置き方ではなく，置いた結果に着目させる」という注意書きをつけてA-2の理由を排除し，一つ分の大きさを決定している．

A-3は「積」のかけ算を手段として「倍」のかけ算の問題を解こうというアプローチである．School Mathematics Study Group (SMSG)が1960年代に提唱し，数学教育の現代化運動とともに消滅したと言ってよい[Anghileri 1988][Link 6Jt][Link 7Et]．授業例も，学術調査に基づく児童の認識の事例も，見当たらない[中島1968a][Mulligan 1992]．
A-4は素朴な発想ながら，[Vergnaud 1983]および[Vergnaud 1988]による根拠付けもある．しかし8〜9歳児では認識が困難とも記されている．1950年代の日本での指導例[中野1957]と合わせて，この考え方は4年または5年で，数量関係の理解を通じて学ぶのが適切である．
A-5はB-5と，A-6はB-6との比較である．ところでB-6は日本限定でなく，韓国でも[Link 8K]，ベルギー駐在員が学校のテストで0点を取った子どもに対し，自分たちは永住するわけではないのだから，「4つずつで5個のカゴ」と考え，式を書く段階でヨーロッパ式の順序にするよう指示したという事例がある．A-5に賛成する記述を含む文献には[小林2012]があり，A-6には[佐藤2010]，B-5には[シューベルト1995]，そしてB-6には[中島1968b][森2009][守屋2011]がある．これらを比較した結果，複数の理由で得られる式を比較して一つを選ぶという指導を含む，B-5およびB-6がより望ましいと判断した．

ここまでA-1からA-6への反論を書いてきたが，だからといって，B-1からB-6までのすべてに賛成するわけではない．B-1およびB-2については，それらを授業で学習しており，それを踏まえた上でのテストであるという条件のもとで，賛成である．この条件が成立していることは，教科書や学習指導案から推測できる．また最近の教育評価論[田中2008]においても，4×8のうち4は1あたり量，8はいくつ分と，区別することの必要性が記されている．
B-3やB-4は，A-2との対比のために挙げたほか，それぞれ指導の実例がある．上に示した例のほか，B-3については，2011年，「2×8ならタコ2本足」と題する授業例が朝日新聞で取り上げられた[Link 9J]．より新しい授業例が[礒田2013]にある．B-4については，あとでもう一つ例を挙げる．反対意見をより少なく見せたい人が編集したら，このB-3とB-4を合わせて1項目にするだろう．
B-5については，算数教育の範囲を超えるが，「5個×3枚」と「3枚×5個」との比較も不可欠である．[Vergnaud 1983]は「4×15と15×4は等しいけれども，4個×15セントによって60セントが得られ60個ではないのはなぜか」と指摘しているが，これは「5個×3枚」「1.5kg×4箱」などをふだんから目にすることのできる，今の日本社会に向けた問題の提案といえる．なお海外で筆者は，「3×80g」「75g×5」と書かれた商品を購入した．かけられる数は単位があり，かける数にはないことで，1個の量はどれだけで，それがいくつあるかを知ることができる．


最後に，B-6について，文化には国際的なものだけでなく，国内の，歴史的な観点が含まれることを挙げておく．いろいろな式の表記や解釈を学び，目の前の問題に対し，子どもたちが答えを出せるようになることを，支援していきたい．

3. かけ算をめぐる状況

3.1 かける数が先の文章題

りんごの問題は，かける数が先に，かけられる数が後に出現し，「かけられる数×かける数＝かけ算の答え」の式で求めることを意図している．この種の出題には，数十年の歴史がある．

把握している限りで最も古い指導例は，1951年の小学校学習指導要領 算数科編（試案）である[Link 10J]．鉛筆の配る本数を求める問題に対し，かけられる数とかける数を逆にした式では，「その数の意味を深く考えもしないで，出てくる順に書き並べ，その間に，かけ算記号を書き入れる」「問題に出てくる数を頭の中にいったん収めて，演算の決定に導くように問題の場を組織だてる力が欠けている」と分析し，3人の2倍で6人になって問題に合わないと指導している．ここでB-4が用いられている．
社会的には1972年の朝日新聞の記事が重要である[Link 11J]．「6人のこどもに、1人4個ずつみかんをあたえたい。みかんはいくつあればよいでしょうか」というテストの出題で，「6×4」の式が不正解となったのに対し，ある子どもの親が学校や教育委員会，そして文部省まで抗議した．数学者であり算数・数学教育にも深い関わりのある遠山啓は同年，科学朝日に記事を寄せ[遠山1972]，トランプ配りを思い浮かべる子どもは6×4＝24と書くのが合理的だと述べ，交換法則や机の長方形配置も挙げて，6×4と4×6のどちらでもよいという立場を示している．
しかしながらその後の算数教育では，かけ算の意味を重視する中で，かける数が先に，かけられる数が後に出現する文章題は，算数教育に携わる教師による書籍で取り上げられ，学力調査・学術調査でも出題されている．教師には，次の2氏の名前を挙げたい．一人は，百ます計算を広めたことで知られる岸本裕史，もう一人は，筑波大学附属小学校で算数を教える田中博史である．それぞれの著書[岸本2003][田中2009]で，子どもたちは十中八九，間違って書くと述べている．
金田茂裕の学術調査[金田2008]によると，その種の文章題に対し，かけ算を学習した後の小学2年生の約20%，大学生の約60%が，かける数×かけられる数の式を書いていた．かけられる数が先に出現する文章題では，大学生の全員，そして児童もほぼ全員が，かけられる数×かける数の式を書いた．
東京都算数教育研究会では，2年に一度，数と計算および数量関係の学力調査を行っており，各学年6万人前後が解答している．2012年度[Link 12J]には以下の出題があった．

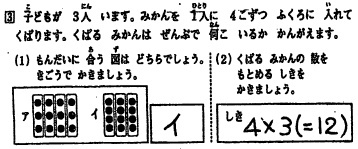
「子どもが 3人 います。みかんを 1人に 4こずつ ふくろに 入れて くばります。くばる みかんは ぜんぶで 何こ いるか かんがえます。」と与えたあと，問題に合う図を2つの中から選択させ，その後，式を書かせている．これにより，文章から場面や数量の関係を適切に把握しているか，および，その関係をかけ算の式で適切に書くことができるかを尋ねている．両方正解したのは54%で，図のみ正解は28%，式のみ正解は6%である．

ここまで見てきた通り，かける数が先に，かけられる数を後に置いた文章題で「かけられる数×かける数」の式のみを正答とする出題は，少なくとも半世紀以上の歴史があり，現在まで継承されている．もちろん，正解不正解を得るに留まらず，その結果は指導にフィードバックされてきた．ところで，その種の出題は低学年までであり，高学年では，わり算が用いられる．2010年度の全国学力・学習状況調査（全国学力テスト）で小学6年生は「8mの重さが4kgの棒があります。この棒の1mの重さは何kgですか」[Link 13J]という問題を解いた．正解となる式は，8÷4ではなく4÷8である．

3.2 a×bとb×a

かけ算の意味を定着させるための指導には，かける数を先に書く文章題の他にも方法があり，また英語の文献でも見ることができる．それは，a×bとb×aの違いを学ぶことである．
まずは教科書を見ておこう．東京書籍の2011年度版では，「えんぴつを 1人に 2本ずつ，5人に くばります。えんぴつは，ぜんぶで 何本 いりますか。」と「えんぴつを 2人に 5本ずつ くばります。えんぴつは，ぜんぶで 何本 いりますか。」を並べて提示している[Link 14J]．いずれも2が先，5が後に出現しているが，状況は異なる．そして順に2×5，5×2と式に表すことが期待される．後者は，かける数が先の文章題でもある．したがって，このペアで式の違いを学習したあと，りんごの問題に「5×3」と書いた児童には，これは「えんぴつを 2人に…」の問題と同じ，と復習することができる．大日本図書による同年度の教科書にも，同様のペアがある[Link 15J]．
ここからは海外の文献を見ていく．AnghileriとJohnson [Anghileri 1988]は，4つずつキャンディを持っている3人の子どもたちは，3つずつキャンディを持っている4人の子どもたちよりも幸運であるという例を使って，「4が3つ」と「3が4つ」の違いを説明している．交換法則についても，それは数の性質であり，3×4が4×3と等しいのは事実だが，日常生活においてそれらが同じとは限らないと述べている．これらはB-2およびB-5と深い関係がある．
純粋な数のかけ算と，算数で答えを求めることとの違いは，VergnaudやGreerも指摘している．Vergnaudの指摘とは，すでに述べた「4×15と15×4は等しいけれども，4個×15セントによって60セントが得られ60個ではないのはなぜか」であり，これは乗法構造を詳述する直前に記されている．Greer [Greer 1992]は，「あるロケットは1秒間に0.85マイルのスピードで進む．16秒ではどれだけ進むか?」なら，子どもたちはかけ算を選ぶが，0.85と16を交換した文章題になると16÷0.85を選びやすいと例示し，実験により認められた「乗数効果」を解説している．ここで乗数効果とは，かけ算で求められると認識・選択することの困難さが，かける数が「整数」「1より大きい小数」「1より小さい小数」のうちどれであるかに依存し，かけられる数の種類には依存しないことをいう．乗数効果は国内でも確かめられている[小原2007]．
「かけ算の順序」の批判者は，しばしば「かけられる数×かける数」は導入時の便法であり，交換法則を学習すれば「かける数×かけられる数」としてもよいと説く（例えば[高橋2011]）．しかしそれでは，上に挙げたVergnaudやGreerの提案や観察を合理的に説明できない．

3.3 「倍」と「積」のかけ算

国内外の文献で，かけ算の分類法をいろいろな人が提案している．その中でも，かけ算を「倍」に由来するものと「積」に由来するものに大別するのが分かりやすい．「倍」は，かけられる数とかけ算の答えが同種の量であり，かける数は単位または助数詞があっても，割合あるいは拡大率とみなして，演算時に無次元となるようなかけ算をいう．「積」は2つの純粋な数どうしのかけ算と，2つの量をかけてそれらと異なる量を得るかけ算からなる．2つに大別した上で，より細かな分類が[Greer 1992]で表になっている．もし3つに分けるのなら，「倍概念」「比例関数」「複比例」が知られている[森1973][Vergnaud 1983]．4つだと，「累加」を加えるとよい[田中2008]．
「倍」と「積」には簡単な識別法がある．a×b＝pで数量の関係が表されるとき，aとbとpがすべて同じ種類の量か，pがaとbのどちらとも異なる種類の量のときは，「積」であり，aとbはpの因数となる（「かけられる数」「かける数」による区別はしない）．pがaとbのちょうど一方と同じ種類の量のときは，「倍」であり，もしaとpが同じ種類の量ならば，aがかけられる数，bがかける数となる．縦×横や底面積×高さによって面積や体積を求めるのは「積」であり，「5個×3枚」や「4個×15セント」は「倍」にあたる．
「倍」と「積」を組み合わせた計算も可能である．10円玉を以下のように並べたとき，その総額はいくらだろうか．そしてどのように計算すればよいか．

縦に見れば30円ずつ，横に見れば40円ずつある．だからといって30×40＝1200と計算してはいけない．現実には120円しかない．10円玉の枚数を数えると，3×4＝12で（4×3＝12としてもよい），12枚ある．これで，金額が求められる．10円玉が12枚で120円というのは明らかだが，式にするなら10×12＝120となる．2つのかけ算の式を合わせて，10×3×4＝120と書くことができる．左辺＝（10×3）×4＝30×4＝120とすれば，30円が4列あることを表現できるし，乗法の結合法則も確かめられる．
10円玉を，おはじきに取り替えると，それは学習指導要領解説にも載っている[文部科学省2008]．その総数を求める式が3×4でも4×3でもよいのは，それはデカルト積に基づいた「積」のかけ算だからである．一方，りんごの出題を含め，議論の対象となっているものは「倍」のかけ算に属する．遠山が1972年に[遠山1972]を書いた時点では，「倍」と「積」の区別が明確化されていなかったと推測できる．認識の変更が，1979年（死去の半年前）の講演録に見られる[遠山1979]．

4. 日本の算数教育の特徴

ここまでの内容を整理するとともに補足を加え，日本の算数教育の特徴を述べる．
最も大きな特徴は，授業の仕方である．授業ごとに「めあて」を教師が設定し，通常45分の授業の中で少数の問題に時間をかけ，1つの問題に全員で取り組む．式や答えを書くだけでなく，その根拠を答えることもある．主となる問題では，その反応（式や求め方など）の多様性を重視する[相馬2011]．この授業方式は『The Teaching Gap』[Stigler 1999][スティグラー2001]により世界的に有名となった．授業は教科書・教師用指導書をなぞって進めるものではないことは，教師が作成している様々な学習指導案から確認できる[筑波2003][Isoda 2007][前川2011][高橋昭2011]．インターネット上で公開されている学習指導案もあり，教師でなくとも，WordやPDFの文書を読むことができる．かけ算の学習においては，B-1やB-2と密接な関係のある学習指導案が多い．
日本は教育先進国であり，教育コンテンツや指導法の輸出国でもある[Link 16J]．算数の教科書を東京書籍と啓林館が英訳して販売しており[Link 17J][Yoshida 2009][Link 18J][Link 19J]，日本の算数教育に関心のある外国の教師・研究者や，海外在住で将来日本に帰国する児童が活用している．
しかしかけ算の順序を含め，日本の方式をそのまま海外に浸透させようというのではなく，各国の言語や文化に対する配慮も見られる．例えば馬場卓也[馬場2002]は，タイ語のかけ算の自然な語順は日本語と同じであるが，教科書の式は英語と同じという観察から，学習者の認知的な負担を指摘し，他の事例と合わせて，教育の国際協力におけるカリキュラム開発の注意点を提示している．また筑波大学とメキシコ教育省の共同事業によりスペイン語の教師向け指導書が作成され[Isoda 2009]，その理論的検討においてxj（xにjを下付き文字で添えた記号）を日本式のかけ算の記号とし使用し，日本語とスペイン語でのかけ算の式の違いを考慮している．
日本の状況に話を戻すと，かけ算については，「かけられる数×かける数」が当然となっている．日常生活においても，寸法や会計は別として，多くの場合，この式を使えば数量を把握できる．「a×b」を「aがb個」と読めばよいからである．ここでaには，数量でないものが書かれることもある．例えばブラウザゲームであるドラゴンクエストモンスターパレード[Link 20J]では，棺桶の絵の右下に「×2」を添え，生き返りを待つ死亡モンスターが2体あることを表現している．
学力調査にも特徴がある．校内の通常のテストや入学試験とは別に実施される，学力調査（学術調査を含む）では，解答者ごとに点数をつけない．児童ごとの正解数や得点よりも，生徒集団の解答類型とその割合を重視し，教育内容の改善に役立てている．そして調査問題は実施後に公開される．全国学力テストは実施後すみやかに試験問題が公表され，数か月後には各問に対する解答類型や正解率を含む表および分析が公開されている（2013年度については[Link 21J]）．
全国学力テストでは「乗数と被乗数を入れ替えた式なども許容する」という注意書きがあるため，かけ算の順序は問われていない．それに対し，東京都算数教育研究会の学力調査では，6年生が解く分数のかけ算の文章題で，「かける数×かけられる数」の式を不正解としている．この例の他にも，高学年では，かけられる数が先，かける数があとに出現する文章題で，2つの数をひっくり返した式を書くと，かけ算の意味を理解していないと判断される事例がある．

5. おわりに

この文書では主に2つのことを実施した．前半では「かけ算の順序」の論点を明らかにしたのち，その論拠となる，正解とする理由および不正解とする理由をリストにした．それぞれの理由は簡潔な記述にすることでわざと曖昧にしており，いくつかの項目間で緩やかに関連させている（A-2，B-3，B-4のように，2つのリストをまたいだ関連もある）．賛成や反対の意見と，このリストとを照合すれば，どの理由を支持しどれを却下しているかが，容易に判断できる．
後半は事例整理であり，これは，かけ算を通じた算数教育の国際理解を意図したものである．とはいえ本記事で紹介したのは，「かけ算の意味」の理解状況や指導に関するアウトプットの，ほんの一部分に過ぎない．紹介できなかったが，1970年代に数学者らが著したいくつかの「量の理論」[小島1976][Nagumo 1977][田村1978]は，現在でも算数・数学教育の基礎として活用できる．英訳された日本の学習指導要領解説[Isoda 2010]と，米国のCommon Core State Standards for Mathematics [Link 22E]との読み比べからも，得られるものが多い．
今後の課題として，算数・数学教育と数学との関わりや，日本の教育と世界の教育との関わりなどについて，文献を整備し，「かけ算の順序」と結びつけた議論に役立てることを考えている．

参考文献

（リリース：2013-11-15 深夜，最終更新：2014-04-05 晩）