わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

アレイ図 (2015.12)

math reprise

目次

  • 1. アレイ図とは
  • 2. 図とかけ算の式
    • 2.1 ひとつ
    • 2.2 ふたつ
    • 2.3 たくさん
  • 3. かけ算の性質
    • 3.1 交換法則
    • 3.2 結合法則
    • 3.3 分配法則の入口
    • 3.4 分配法則
  • 4. アレイ図の応用
    • 4.1 長方形配置の周りの数
    • 4.2 十円玉のアレイ図
    • 4.3 ななめ
    • 4.4 L字型
  • 5. 雑多な話題
    • 5.1 限界
    • 5.2 教具
  • 6. アレイ図いまむかし
    • 6.1 文献から
    • 6.2 教科書
    • 6.3 かけ算の順序論争
  • 参考文献

1. アレイ図とは

アレイ図とは，同一のものを，長方形のように配列してできる図のことです．以下がアレイ図の例です．

●●●●
●●●●
●●●●

「長方形」という言葉を使わずに，説明するなら，同一のものを「縦横に規則正しく並べた図」[Link 1]と言うことにしましょう．
「同一のもの」には，丸印（●または○）がよく用いられますが，四角（■または□）にすることもあります．一辺の長さが1cmの正方形を用いれば，長方形・正方形の面積を求めることにも活用できます．
小さな注意点ですが，アレイ図で数を勘定する対象となる一つ一つが「アレイ」なのではありません．それは「ドット」「対象物」などと呼ばれます．シールやおはじきなどを対象物として，子どもたちが作ったり手にとったり，動かしたりすることもできます．
次の形は，「長方形のように配列」していますが，アレイ図とは呼ばれません．

●●●●
●　　●
●●●●

また次の形は，「縦に3つ，横に4つ並べた形」と言えますが，これもアレイ図にはなっていません．

●●●●
●
●

名称ですが，「アレー図」「ドット図」とも呼ばれます．[新算研2011]には，「長方形配列」「長方形的配列」と書かれている，昭和50年代の論説が入っています．なお，アレイ図の英訳はrectangular arrayが一般的です．
「アレイ(array)」を日本語に訳すと，「配列」です．プログラミングでよく用いる，重要なデータ構造です．ただしプログラミングの配列は，基本的に1次元であり，配列の配列なら「2次元配列」「多次元配列」などと呼びます．そちらを基準とするなら，算数のアレイ図は，2次元の配列のみを考えます．

本記事は2012年1月に作成したもの[Link 2t]の改訂版となります．アレイの応用問題と，歴史的な話（「かけ算の順序論争」関連を含む）を充実させ，参考文献・URLを末尾に集約した点が，主な変更箇所となっています．

2. 図とかけ算の式

2.1 ひとつ

以下の図を対象として，この●の個数を表すかけ算の式を考えてみます．

●●●●
●●●●
●●●●

かけ算の式は，3×4とするのが一般的です．面白いことに，「かけられる数×かける数」を採用する日本でも，「multiplier × multiplicand」を採用する米国などでも，同じ式です．
日本ではこの図を次のように分けて，一つ分の大きさを3とし，それが4つあるので，3×4＝3＋3＋3＋3＝12と考えます．

●｜●｜●｜●
●｜●｜●｜●
●｜●｜●｜●

この記事では，「一つ分の大きさ」と「かけられる数」を同一の意味で用いています．算数教科書の，かけ算の導入では「1つ分の数」と書かれます．「かける数」に対応する用語は「いくつ分」です．「一つ分の大きさ」とし，「一つ分」と表記しない理由は2つあります．「一つ分の大きさ」「幾つ分」が，『小学校学習指導要領解説算数編』で用いられています．そして，かけられる数は小数や分数になっても，かける数が整数であれば，かけ算は累加で求められるのに対し，かける数を小数などになる際には，そうはいかず，意味の拡張を必要としまして，その点からも，かけられる数とかける数の区別をしておくべきだという考えからです．「一つ分の大きさ×いくつ分」は，低学年のかけ算の文章題にも，アレイ図やそれに関連する形状の計数にも，活用ができる，というのが，この節のみならず記事全体の基本方針となります．なお，アレイ図のかけ算を学習すれば，あるいはアレイ図を思い浮かべれば，「一つ分の大きさ×いくつ分」にこだわらなくていいのでは，という考え方の紹介などについては，6節で取り上げます．
それはともかく米国では，もとの配置を横方向に切り分けて[Bennett 2011] [Link 3]，以下の図のようにしてから，「3つの4 (three 4s, three times four)」と解釈し，3×4＝4＋4＋4＝12とします．

●●●●
――――
●●●●
――――
●●●●

アレイ図の縦方向の個数を先，横方向の個数を後に書くという慣習は，長方形の面積の公式を縦×横で表すことや，大学で行列のサイズや成分を示すときの素地となります．

2.2 ふたつ

アレイ図は，また長方形的なものは，必ず縦×横なのかというと，そうとは限りません．今このページをご覧いただいている，パソコンまたは何らかの機器の，画面サイズはいかがでしょうか？ 筆者のは，1920x1200です．幅が1920ドット，高さが1200ドットです．そして幅は横方向を，高さは縦方向を表します（先に長いほうを，後に短いほうを書く，というやり方もあります[伊藤2009] [Link 4t]）．
算数の取り扱いを考えると，横×縦も，長方形の面積とするほうが，都合がよさそうです．ひとつ例を挙げると，平行四辺形の面積，すなわち底辺×高さを導くときに，被乗数を長方形の横の長さに対応づけておけばスムーズにいきます．なお，長方形において縦と横は同時に発見できるのに対して，平行四辺形の場合は底辺を選択することでその高さが決まるという違いがある[Link 5t]のには，注意したいところです．
アレイ図におけるドットの勘定，またアレイ図とかけ算の式の対応付けについても，同様にします．結局のところ，2.1節の最初に挙げたアレイ図に対して，●の総数を求めるかけ算の式は，3×4＝12でも，4×3＝12でもよいという次第です．
ただし，日本の算数において，なぜ「4×3」がこのアレイ図を表す式になるのかは，米国で3×4になるところで図示した，以下の切り分けを理由とします．

●●●●
――――
●●●●
――――
●●●●

こうすると，一つ分の大きさが4で，それが3つ分あると認識でき，4×3＝4＋4＋4＝12となるわけです．
1つのアレイ図に対し，2種類のグルーピングができるのは，[筑波2012]にある次の図からも，知ることができます．

「1つのアレイ図に対応するかけ算の式が2種類ある」を「1つのかけ算の式に対応するアレイ図が2種類ある」と解釈したとき，これを積極的に活用した授業例もあります[Link 6]．教師が「アレイ図カルタ」を開発しました．カルタの場札は，1×1から9×9までのアレイ図のカードです．教師が，かけ算の式が書かれた読み札を読み上げ，児童らがその式に合う場札を取ります．しばらくしているうちに，ある児童から「2×3と3×2は，カード（アレイ図）の向きがちがうだけで，同じなのにお手つきはおかしい」という声が出ます．これは教材開発者の意図なのでした．授業ではそれ以降，かける数とかけられる数を入れ替えたものでもOKとしました．

2.3 たくさん

かけ算は「一つ分の大きさ×いくつ分」で表される，あるいは，累加の簡潔な表現である，という前提に基づくと，

●●●●
●●●●
●●●●

というアレイ図で，もっと別の「一つ分の大きさ」があるのではないかと，考えることができます．具体的には次のとおり．

  • 一つ分の大きさを2個とし，それが6つある状態，式だと2×6＝2＋2＋2＋2＋2＋2＝12
  • 一つ分の大きさを6個とし，それが2つある状態，式だと6×2＝6＋6＝12
  • 一つ分の大きさを1個とし，それが12ある状態，式だと1×12＝1＋1＋1＋1＋1＋1＋1＋1＋1＋1＋1＋1＝12
  • 一つ分の大きさを12個とし，それが1つある状態，式だと12×1＝12

「a×b」で表せる式が他にないのは，12の約数が1, 2, 3, 4, 6, 12だからです．負の数や小数・分数は，アレイ図で表現できないので，対象外としておきましょう．
2×6は，12人が仲良く（ニコニコで）並んでいる状態と解釈できます．例えば以下の図です．

ＡＡＢＢ
ＣＣＤＤ
ＥＥＦＦ

他の式でも，「一つ分の大きさ」と「いくつ分」を視覚化できます．実際，[筑波2011]のかけ算の最初の授業（板書例）では，以下のとおり，「3こずつ4つ分」や「2こずつ6つ分」も複数の取り方ができることを示しています．

とはいえここで，見直しが必要でしょう．問題解決学習における「練り上げ」です．いろいろ出たけど，さてどうしましょう?
まず，1×12や12×1を，式としては認める（実際，積は12ですし）としても，図と結びつけるのには無理があるように感じます．
それを言い出すと，あの図から2×6や6×2を連想させよというのがナンセンスという主張だってできます．国語的には，より正確にはコミュニケーションとして考えるなら，次の例と結びつけられそうです．辞書で「犬」の意味を調べたあと，先生または親が「これは何?」と犬の絵を見せたとき，子どもが「食肉目イヌ科の哺乳類。嗅覚・聴覚が鋭く…」[Link 7]と答えられるよう，育てたいわけではないということです．

比較に使えるのは，文部科学省が発行している『小学校学習指導要領解説算数編』（書籍として購入できるほか，[Link 8]よりPDF版を無料で入手できます）です．この文書では，アレイ図から話を始めていません．「12個のおはじきを工夫して並べる」という活動を例示し，そこで得られる形状が，以下の2種類のアレイ図だとしています．

「12個のおはじきを工夫して並べる」というとき，1×12や12×1は，並べ方としてはあり得るけれども，「工夫して」の観点では，良いものとは言えません．
「さてどうしましょう」に対するよい結論，言い換えると一本化は，難しいようにも思います．アレイ図が与えられたとき，どんなかけ算の式と結びつけられるかについては，状況によって異なります．いろいろ目にしてきた限り，日本の小学校では，「1種類（縦×横）」「2種類（縦×横，横×縦）」「多数」が，その状況に合わせて採用，使用されています．
海外では，Webでざっと見た印象として「1種類（縦×横）」が多く，ついで「1種類（横×縦）」で，2種類以上というのは見かけませんでした．
以降では，特に断りのない限り，アレイ図に対応する乗法の式として「縦×横」のみを使用することとします．

3. かけ算の性質

被乗数および乗数が正の整数のとき，交換法則・結合法則・分配法則などが成立することを，任意の正整数に対する証明（代数的な証明は，例えば[高木2008]を参照してください）のかわりに，特定の値について図から確認していきます．

3.1 交換法則

次の図は3×2＝6です．サイコロの6の目みたいですね．

●●
●●
●●

次のようにすると，2×3＝6となります．

●●●
●●●

「次のようにする」方法には，いくつかあります．

  • 2個を移動させる（一般に，a行b列（ただしa＞b）のアレイ図からb行a列のアレイ図を得るには，b行b列の「部分アレイ」は動かさず，（a−b）行b列の「部分アレイ」を移動することでできます）．
  • 90度回転移動させる．
  • 転置(transpose)させる[Link 9t]．
  • 図形はそのままで，見る側が90度回転する．

「●」の数は変わりませんので，3×2＝2×3となります．式からだと，上に書いた2つの等式を結びつけて3×2＝6＝2×3とし，真ん中を取り除けば，3×2＝2×3を得ます．

3.2 結合法則

次の図は，「3×2」のアレイを「一つ分」とし，それが4つあるので，（3×2）×4＝6×4＝24となります．

●●　●●　●●　●●
●●　●●　●●　●●
●●　●●　●●　●●

間の空白を詰めると，一つのアレイ図になります．3×8＝24です．

●●●●●●●●
●●●●●●●●
●●●●●●●●

2つの図を見比べると，8を「2が4つ」と考えることができます．これにより，3×8＝3×（2×4）を得ます．
以上を式の上で整理すると，（3×2）×4＝3×（2×4）が言えます．違う順序でかけても，答えは同じになるという次第です．
結合法則の視覚的表現には，上記のほかに，直方体を用いる方法[Anghileri 1988] [Vorderman 2010] [Link 10t]や，長方形配置の箱それぞれに同数のものを入れるという方法[Link 11t]もあります．それぞれ1枚ずつ，イラストを貼り付けておきます．


3.3 分配法則の入口

分配法則の前に，『小学校学習指導要領解説算数編』に書かれている，「乗数が1増えれば積は被乗数分だけ増える」という性質を確認しておきます．次の2つの図で表されます．

●●●●●
●●●●●
●●●●●
●●●●　●
●●●●　●
●●●●　●

上のアレイ図は3×5＝15ですね．下は「アレイ図と，線」と考えることで，3×4＋3＝12＋3＝15となります．等式は，3×5＝3×4＋3です．
アレイ図を，たし算（合併）だけでなくひき算（求残）で考えることもできます．具体的には，「乗数が1減れば積は被乗数分だけ減る」として，縦方向の3個の●を順々に取り除いていくと，3×1＝3，3×0＝0を得ます．0×3は累加で計算できる（0×3＝0＋0＋0＝0）のに対し，3×0＝0は累加による意味づけが困難ですので，アレイ図で「減らしていく」のは，積が0になるのを理解するための一つの手段となります．

3.4 分配法則

図は次の2つです．

●●●●●
●●●●●
●●●●●
●●●　●●
●●●　●●
●●●　●●

上の図は3×5＝15です．下の図から，2つのアレイ図の合併を考えることができ，式は3×3＋3×2＝9＋6＝15です．これにより，3×5＝3×（3＋2）＝3×3＋3×2が導かれます．
被乗数を分けるタイプ，被乗数と乗数の両方を分けるタイプの分配法則もありますが，省略します．

4. アレイ図の応用

4.1 長方形配置の周りの数

冒頭で「アレイ図ではない」とした図を再掲します．

●●●●
●　　●
●●●●

「●は全部でいくつあるでしょう」という問いに対して，かけ算を使った式がいくつかできます．
思いつく式を書いておきます．アレイ図のほか，「一つ分の大きさ×いくつ分」を使用しているものもあります．

  • 4×3−2＝12−2＝10
  • 4×3−2×1＝12−2＝10
  • 3×3＋1＝9＋1＝10
  • 3×2＋2×2＝6＋4＝10
  • 4×2＋1＋1＝8＋1＋1＝10

類題が[筑波2011]に見られます．

4.2 十円玉のアレイ図

別の応用として，アレイ図なのですが，その対象物は10円玉，100円玉などの硬貨（紙幣でもかまいません）で，その総額を求めるという問題を作ることができます．
「●」を十円玉に置き換えて，次のように並べたら，ぜんぶでいくらでしょうか．

30円×40円＝1200円としてみれば，大金持ちになった気分です．現実は，例えば10×3×4＝120でして，120円です．詳しい解説は，[Link 12t]をご覧ください．

4.3 ななめ

次の配置で，○の総数を求めてみましょう．[研究の会2010]によると，これは「平成元年に日米の数学的問題解決能力を比較するために，両国の小学校4年生に出題された問題」とのことです．


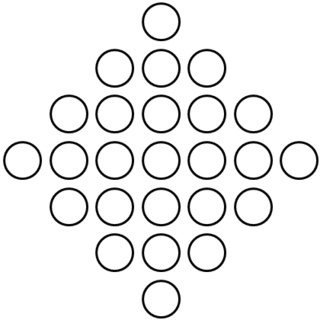
図からアレイは自明ではなく，かけ算で求める必要もありません．
とはいえ次のように，角の4つの○を動かせば，5行5列のアレイに早変わりします．そうすると，5×5＝25によって求められます．

別の方法でも，アレイが出現します．もとの図を45度，回転させてみます．

そうすると，4×4の配置と，3×3の配置が，重なっているのが見えてきます．式は4×4＋3×3＝16＋9＝25によって，総数を求めることができるというわけです[Link 5t]．

4.4 L字型

アレイ図を用いた応用問題の最後に，L字型の配置を紹介します．問題文と解答例は以下のとおりです．

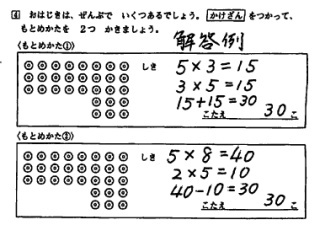
もとめかた①は，左の5列と右の3列に分けてから，それぞれを縦×横で求め，足し合わせた式となっています．それに対し求め方②では，5行8列のアレイから，2行5列のアレイを取り除くという考え方で，かけ算，かけ算，ひき算の式にしています．
上記は，東京都算数教育研究会（都算研）が2年おきに実施している，数と計算・数量関係の学力実態調査からです．表示の都合上，平成22年度実施分[都算研2011]を用いましたが，24年度と26年度にも同様の出題があり，各回，5万人以上の児童が解答しています．調査人数（解答者数）や出題とともに，正解率も公表されていて，完答（2つの適切な求め方を書く）は70%前後，1問正答は10%ほどとなっています．

半具体物による1つの場面に対し，複数の考え方，そして式が得られるため，アレイ図そのものよりも，式を求める問題として，よく活用されている印象があります．
L字型の配置については，1989年の東京書籍の算数教科書を英訳したものを紹介するというトーク[Yoshida 2009]でも，紹介されています（2年です．アレイ図を用いた交換法則の学習は，3年となっています）．L字型のほか，市松模様による丸印の配置で数を求めるという指導事例が，[久保2004]に見られます．

5. 雑多な話題

5.1 限界

アレイ図は，乗法の構造を理解しやすくするツールでありますが，頼りすぎるのも，問題があります．
まず，アレイ図は，被乗数・乗数とも，正の整数を対象とします．例えば0×3や4×0を（この2つを区別するような）アレイ図で表すのは，困難です．整数から小数・分数への拡張は，「●」による離散量から，単位正方形に代表される連続量に置き換えれば，可能ですが，負の数や無理数[中島1968]，また複素数や四元数[宮下2011]と拡張しても，大丈夫でしょうか．
別の観点での課題が，これまで書いてきた中から見ることができます．3.3節で取り上げた，次の2つの図です．

●●●●●
●●●●●
●●●●●
●●●●　●
●●●●　●
●●●●　●

等式は3×5＝3×4＋3です．左辺は一つの長方形，右辺は一つの長方形と一つの線分の和，であるように見えます．
そこの何が問題なのかというと，「a×1を表すアレイ図」が，「a個を縦方向に並べたもの」と区別できない点です．なので，子どもたちに，1次元の量と2次元の量の区別がきちんとつくのかなという疑問が生じます．
なお，長方形の周りの長さを求める式を選ばせ，面積ではないことを確認する出題が，平成19年度の全国学力テスト[Link 13]に見られます．
あと一つ，結合法則について，交換法則・分配法則に比べ，表現や解釈に手間を要します．というのも，結合法則を表すための場面をアレイ図で描き，式を立ててみると，アレイのかけ算（積の乗法）だけでなく，「一つ分の大きさ×いくつ分」あるいは倍概念（倍の乗法）も根拠とせざるを得ないのです（[坪田2015]に載っている結合法則の説明では，式に「いくつ分×一つ分の大きさ」も用いています）．直方体のように3次元を扱おうとすると，体積はより上の学年での学習となります．
結局のところ，アレイ図のみで乗法の諸性質を示そうというのには無理があります．それに対し，累加で意味づければ，代数的に証明できますし，アレイ図の総数計算も累加で行えます．累加や倍の乗法をきちんと理解した上で，アレイ図・面積図を用いた積の乗法へと学習を進めていくのが良いように思います．

5.2 教具

ここではアレイ図に似た教具を探し，比較を試みます．
まず思い浮かぶのは，九九の表です．罫線をなくし，縦方向をきちんとそろえて出力するのは，プログラミング課題として効果的ですね．

ですが，これをアレイ図と同一視するわけにはいきません．表示範囲を「3×4」に限定させてみると分かるのですが，マスの数がなぜ12なのかが，明瞭ではありません．

「1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12と数えさせるのか?」「数字が間違っていたらどうするの?」といった疑問が思い浮かびます．
数や図形の感覚を豊かにするには，情報（数字など）をすべて見せるのではなく，ない状態から発見させること，2つあるいはたくさんある中で違いを識別できるようになることが，重要となってきます．そうすると，九九の表（早見表）と，アレイ図には，別の役割を持たせて使うのが妥当と言えます．なお，アレイ図は交換法則に目が行きがちですが，2×3と4×6のアレイ図など，拡大・縮小・相似を学ぶことにも活用できます[田中2009]．
アレイ図と似ており，手を動かして学習できる教具に，「かけ算マシーン」（現在，この言葉で検索すると，雑誌の付録についたという別のものが上位に出てきます）があります．数学教育協議会の活動・著書でよく見られる「かけわり図」に基づきます．出来上がりは次のとおりです[銀林2011]．

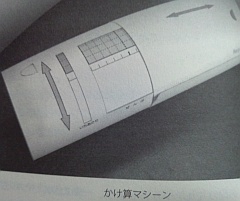
筒状ではなく平面を使った同種のものは，[Link 14] [Link 15]にあります．
TOSSで開発された「かけ算九九計算尺」が，ネット通販で購入できます[Link 16]．左下を1×1とする九九の表を台紙とし，かぎ形の枠（透明シート）を乗せることで，2×3や7×8が一目でわかると謳っています．番号を振らず，また左上を1×1としていますが，類似したかぎ形の枠を用いた教具を，水道方式の解説書[遠山1961]で見ることができます．
「実物大九九カード」の作成や活用が，[田中2005]に書かれています．九九といっても，数字は一切出てきません．これは，1枚のカードに，丸形のシールを貼り付けて作る，アレイ図です．同じ列は同じ色のシールとすることで，見た目がきれいで，しかも，「一つ分の大きさ」が分かりやすい教具となっています．

6. アレイ図いまむかし

6.1 文献から

「世界最古のアレイ図」「日本最古のアレイ図」というのは，探してみると面白そうです．
把握している限り最古のものは，明治時代の算術の本です[寺尾1888, コマ番号30] [Link 17t]．

「1」を5行3列に並べた図を載せ，五と三といふ二つの数あらんに、三に五を掛けたるものと、五に三をかけたるものとは、互に相等し」と解説しています．もちろんこれは乗法の交換法則の話であり，「乗数と被乗数とを交換しても、積はかはらずといふことを得べし」とも記されています．
明治時代の終わりには，数学者として知られる高木貞治も取り上げています[高木1909, コマ番号33] [Link 18t]．

アレイの各要素を「●」で表現し，次のページで，「積は因数の順序に関係なし。」を大きく書いています．
ただし，ここで交換法則を理解したとしても，それまで，a×bと表していた場面について，b×aでもよい，とはなりません．同じページの脚注に「被乗数が名数なるときは，其単位の名を去りて後，此法則を適用すべきこと勿論なり。」とあります．交換法則は，不名数（現在なら「無名数」「純粋な数」「無次元量」になるでしょうか．[Anghileri 1988]でも，交換法則は純粋な数における性質であり，日常生活においては話が違ってくると指摘しています）における性質だというわけです．
このことは，同書のあとのページで，被乗数や乗数を小数に拡張して，かけ算を考える際の記述からも，裏付けられます．今でいう小数×整数の場面で，「積の単位と被乗数の単位とは必ず相同じ。」が，大きな文字になっています．小数どうしのかけ算にも，同じ趣旨の注意書きがあります．「被乗数×乗数」で表されるかけ算のモデルと，「因数×因数」で表されるかけ算のモデルがある，と考えれば，例えば[Greer 1992]で集約されているモデルと整合します．
アレイの使用例について，20世紀後半に話を進めます．1960年代の算数・数学教育を見直す際，米国のNew Math，日本では「数学教育の現代化運動（現代化）」を無視できません．New Mathをリードした団体はSchool Mathematics Study Group (SMSG)です．かけ算・わり算の学習[Link 19]がアレイ図で始まっており，縦の数をrow，横の数をcolumnとして「rows × columns = elements」という式へと導いています．アレイの1要素は，中点（・）や正方形（□）が用いられています．正方形の小片を隙間なくつなぎ，大きな長方形または正方形で描くものが大部分ですが，小さな（隣同士に隙間のある）正方形を並べている図も見られます．
米国の論争を紹介する中で，アレイ図を紹介している文献に，[中島1968]があります．そこでは，「6×9を次のような配列（の点の個数）を意味するとして定義するのがアレイの考えである．」と書き，手書きと思われる図を添えています．

この図と「6×9」を結びつけるのに，直積を用いています．直積の定義を述べたあと，「A＝{a,b,c}，B＝{x,y}のとき，A×Bは次の図で格子点で表わされるものの集合にあたる．」とあります．そこに載っている図も，次のとおり，手書きであるように見えます．

「集合」もまた，New Mathそして現代化のキーワードでした．現代化については，[杉山2012]で「終わった」段階での概括（1994年に書かれた論文）を読むことができます．直積（デカルト積）に基づく国内外のかけ算の事例は，[Link 20t]をご覧ください．
SMSGと別に，正方形の小片に基づくアレイが，日本では同じ時期に活用されていました[遠山1961]．正方形やアレイではなく，「タイル」と呼びます．もともとは，10や100を視覚化したり手で操作したりするという，位取りのためのツールでした．縦にも横にもくっつけられるという特長を生かし，長方形配置によるかけ算の図式化に転用していったと考えられます．

例えば3×4＝4×3の等式は，下図のようにタイルの切り分けによって表現できます．


長方形になるよう並べたタイルは，交換法則の学習時を除き，縦の枚数がかけられる数，横の枚数がかける数として，式に表すのが慣例となっています．その左や下に，数量や目盛りなどを添え，左側（縦の数量）を「1あたり量」，下（横の数量）を「土台量」に対応づけ，1あたり量×土台量によりかけ算の意味を示すようにもなりました[銀林1975]．
数学教育協議会とTOSSは，基盤となるものがずいぶんと異なるものの，それぞれに賛同する教師が少なくありませんし，出版物も豊富ですので，算数教育において一定の影響力を持つ団体と言えます．5.2節で教具を取り上げる際に，この2つの団体を引き合わせましたが，アレイの問題についても，興味深い対比がなされています[Link 21t]．
数学教育協議会を結成し，その委員長を務めた遠山啓は，ミカンを使った文章題に対し，正解となるかけ算の式が一つだけというのがおかしい根拠として，トランプ配りを挙げたあと，「これが，もし，つぎのような問題だったら，どうだろう．『教室の机は1列に6つずつ4列ならんでいます．机はみんなでいくつありますか』という問題では，4×6でも，6×4でもいいとせざるをえないだろう．」と記しています[遠山1978]．
それに対し，[向山2004]には，「こしかけを ならべています。1れつに4こずつ 5れつ ならべると，ぜんぶでなんこになりますか。」という出題が入っています．正解となる式は「4×5＝20」のみです．
こしかけの問題と，机の問題が，まったく同じ構造となっています．
とはいえ違いもあります．大きな相違点は図の有無です．こしかけの問題には図もあります．列ごとに空きが設けられていますが，同じ列のこしかけの間隔は，ほとんどありません．それにより，4個ずつのグルーピングができ，「4こ」がかけられる数，「5れつ」のほうがかける数，と区別されます．それに対し，[遠山1978]が挙げた机の問題には，図は見当たりません．
「1あたり」を重視する数教協のスタンスのもとで，机の問題は「6つ/列×4列」と書くのが自然ですから，その点でも，配る問題とアレイを結びつけようとするのは，「過去の話」と判断せざるを得ません．
図なしのアレイの文章題は，米国のコモンコア（Common Core State Standards，各州共通基礎スタンダード）からも見ることができます[Link 32] [高橋2012]．3×6の式で求める文章題は，"There are 3 rows of apples with 6 apples in each row. How many apples are there?"（6個ずつ3れつにならんだリンゴがあります．リンゴはいくつありますか）です．そこには，rowだけがあって，columnが見当たりません．表の脚注に，"The language in the array examples shows the easiest form of array problems. A harder form is to use the terms rows and columns: The apples in the grocery window are in 3 rows and 6 columns. How many apples are in there? Both forms are valuable."（アレイの例題で書いたものは，アレイの問題の中で最も簡単なタイプです．「食料品店の陳列窓に，リンゴが3行6列で並んでいます．リンゴはいくつありますか」のように行と列を使うと，もっと難しいタイプになります．どちらのタイプも重要です）と書かれています．
アレイ図は2次元的な配置であり，そうすると，行と列（rowとcolumn）を使って説明するのが自然ではありますが，子どもたちがかけ算の場面と認識したり，式に表したりするとなると，必ずしもその2つを使わず，rowのみを使ってもアレイの場面が記述でき，かつそれがより簡単だ，というわけです．「easiest」「harder」の根拠は，コモンコアの文書内で書かれていません．フランスにおいて直積による意味づけでは学習に支障をきたすという[Vergnaud 1983]の指摘が，米国のかけ算の学習においても当てはまるのではないか，と考えることができます．
最後に，2010年代に出版された洋書[Vorderman 2010]とその邦訳[ヴォーダマン2012]を通じて，同じ場面に対する式の違いを見ておきます．どちらの本にも，以下のとおり，人型のアレイ図（クォータービューなのは，これまでの本で見かけません）に対して，2つの考え方（式）が可能としています．


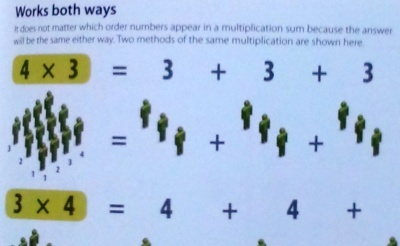
ここで確認しておきたいのは，かけ算の式の解釈です．英語で書かれた[Vorderman 2010]では，1番目の式が4×3＝3＋3＋3＋3＝12，2番目の式が3×4＝4＋4＋4＝12なのに対して，和訳[ヴォーダマン2012]では，順に3×4＝3＋3＋3＋3＝12，4×3＝4＋4＋4＝12です．国ごとの事情を考慮して，かけ算の式が変わっているわけです．

6.2 教科書

日本と中国の教科書事情を取り上げます．日本では，小学校の算数教科書が，平成27年度に改訂されました．その前年（2014年）に催された教科書展示会で，検定済みの教科書を見る機会がありました[Link 22t]．
アレイ関連については詳細を記録していませんでしたが，覚えていたことを簡単に記すと，2年でも，縦横に並んだロッカーの配置など，アレイ図に似た状況がイラストになっていまして，そこからかけ算の式を求めるという出題もありました（筆者の期待としては，そこでは縦×横でも横×縦でも正解としたいところですが，教科書からは必ずしも，両方正解となるのか，一方だけなのかは，読み取れませんでした）．交換法則を2年で学習しますが，その段階では，九九の表から見つける「きまり」となっています．交換法則をきちんと学ぶのは3年で，アレイ図を，縦から・横から見ることで導出するというのが多かったように思います．
教科書は，学習指導要領に依拠して作成され，検定されています．上で，『小学校学習指導要領解説算数編』には，「12個のおはじきを工夫して並べる」という活動において，「●」を2行6列や3行4列に並べたアレイ図が載っていることを述べましたが，これは1999年の解説[文部省1999]にも見られます．
アレイ図とともに中国の教科書の記載を，[高橋2011]が取り上げています．「×の前は被乗数なのか乗数なのか，などという（無用な）ことに頭を悩まさないで，×の前も後も同じ因数であり，式は，3×2でも2×3でもどちらでもよい，という教え方です」とあるとおり，著者はこの件を肯定的に捉えています．
中国のかけ算の指導に関して，アレイ図ではなく，5色の風船が3セットというイラストとともに，5×3でも3×5でもよい（「被乗数と乗数の区別をなくし，最初から因数として扱う」）という事例もあります[国教研2009]．ですがそこでは，現場授業を観察した結果として，「量の扱いではやはり不具合があって，教師たちの丁寧な対応によって乗り越えているところである」という課題も指摘しています．

6.3 かけ算の順序論争

かけ算の順序論争におけるアレイ図の使われ方について，Webの情報をもとに，古いものから紹介していきます．
1990年代から「かけ算の順序」の問題を指摘してきた東北大学の教員が，2010年に公表した中に，「■」や「●」，また「足」を並べたアレイ図を見ることができます[Link 23]．
また別に，批判する人が，かけ算を認識する際の2種類のメンタルモデルを提案しています．そのモデルの1つは「アレイ・グリッド　モデル」と呼ばれ，文章題を解く際に，アレイをイメージしているといいます．この提案は，あるWiki上で2011年12月に書かれたものが初出ですが，このWikiは一時期荒らされ，現在は別のところで公開されています[Link 24]．
Wikipediaに「かけ算の順序問題」の項目ができたのは，2012年10月25日です[Link 25]．当初から，学習指導要領解説のアレイ図の件が書かれていました．
アレイ図で考えれば，2種類の式が得られるという主張に対して，当ブログでは，なぜそれが国内外の算数教育で受け入れられていないかを明らかにしてきました[Link 26t]．その理由は，「a×bとb×aという，2つの式の意味（それぞれの式が何を表すか）の違いを，授業を通じて重視している」「アレイやタイルによる導入・意味づけでは，子どもたちがその後の学習で苦労する」の2点に集約されます．a×bとb×aの違いについて，海外の授業例は，[サルカール アラニ2010] [Link 27t]で読むことができます．その後の学習で苦労の一例は，前述の中国の状況です．日本[遠山1981]やフランス[Vergnaud 1983]でも指摘があり，[Link 28t] [Link 12t]で整理を試みました．
アレイやかけ算の順序を巡っては，2015年，海外で1枚のテスト用紙をもとに，盛り上がりを見せました[Link 29]．「4×6」に対し，アレイ図を描いてから答えを求めなさいという出題です．鉛筆書きの答案は，6行4列の「1」ですが，不正解とされ，その右に，4行6列に並べられた「1」が赤で書かれていました．
この件は，イギリスのインディペンデント紙が批判的に報じています[Link 30]．不正解に賛成寄りのブログ記事をもとに，当ブログ上で情報の整理と紹介を試みました[Link 31t]．

参考文献

以下はWebの情報です．番号のあとに「t」がついているものは，筆者が作成しました．

（最終更新：2016-01-03 深夜）