目次
1. はじめに
2. 《倍の乗法》と《積の乗法》
3. アレイの認識
4. 《積指向》とその課題
5. おわりに
参考文献
1. はじめに
2021年は,「かけ算の順序」に関して豊作の年となった.
出版物では,「かけ算の順序・かけ算の種類」を章題とする書籍[谷口2021]のほか,かけ算の出題に対し懐疑的・批判的な視点で述べたものが刊行された[小林2021][坂間2021][野﨑2021].これらの書籍情報と,インターネット上で公開されている記事などへのリンク集を,[Link 20211122]に設けた.
教育行政においては,東京都の日野市教育委員会で2021年2月,「かけ算の文章題において、式の順序を固定するか否かの見解を、その理由とともに誰でも見える形で公開してほしいに関する請願」が審議され不採択となり,その議事録要旨が公開された[日野教委2021][Link 20220415].
学術における2021年の動きとしては次の2点がある.一つは,日本数学教育会・日本数学教育学会の各論文にDOI(デジタルオブジェクト識別子)が割り振られ,PDFファイルがJ-STAGEで無償ダウンロードできるようになったことである.もう一つは,日本科学教育学会第45回年会がオンライン開催され,「比例・乗法概念に関する教授・学習に関する研究開発Ⅱ」の課題研究発表として5名の発表があった点である[Link 20220428].複数の発表題目に「乗数・被乗数の順序問題」の表記が見られ,その一つ[礒田2021]では導入部に「小2子弟の立式」を取り上げている.
筆者は,「6人のこどもに、1人4こずつみかんをあたえたい。みかんはいくつあればよいでしょうか。」に対し「6×4=24」の式を不正解にすべきかどうか[Link かけ算の順序問題]を,「かけ算の順序問題」と捉えるのには反対である.かけ算の学習において「順序」は,「かけ算では,じゅんじょをかえてかけても,答えは同じになります。」のように,第3学年の結合法則で使用されている[Link 20140705].誤解を減らすための代わりの表記は「被乗数と乗数の順序」であり,[文部科学省2018]や[中原2011]では肯定的な文脈で使用されている.その一方で「小学校では,例えば乗算における被乗数と乗数の区別や順序をやかましく指導することすらあると聞く」を含み批判的な文章が[森村1979]に見られる.
名称は別にして,「6×4=24」の式を不正解とすることに賛成である.論拠を整理[Link 20131116][Link 20191031]したうち(対象物と数値を上記のものに変更して)「この問題では,1人あたりのみかんの数がかけられる数であり,与える人数がかける数となる.」および「6×4と4×6は,かけ算の答えは同じでも,意味は異なる.」に共感を持ち,教科書・書籍やインターネット上でアクセス可能な学習指導案などを通じて,第2学年のかけ算の単元で学習していることを把握している.[齋藤2013]および[藤井2015]はそれぞれ,数学的背景(理論)をもとに小学校算数の指導内容を解説しており,「かけ算の順序問題」についても言及が見られる.現在の学習指導要領のもとで乗法の学習の本質をなすのは,被乗数を単位量としたときの乗数倍になるというスカラー関係[中島1968][Vergnaud 1983][Lannin 2013][Link 20211030]であり,他の場面のかけ算は,スカラー関係を直接的または間接的に適用することで,立式や公式化がなされるものとなる.
本稿では,かけ算で求められる場面のうち「積」に着目する.ただし,かけ算の結果として求められる値ではなく,かけ算の場面における「倍」と相対する概念である.2年の算数教科書にも,おはじきの並びなどで出現する.
インターネット上では,「積」に基づく認識により,上述のみかんの文章題で「6×4=24」も「4×6=24」も正解とすべきという主張をよく見かける.
対象と手段に着目することで,《倍の乗法》《積の乗法》《積指向》《倍指向》の4通りに分類し,国内外の事例を照合して検討を行う.結論としては,《倍の乗法》《積の乗法》も,日本の算数教育では《倍指向》に基づき立式の根拠が説明可能となっている.《積指向》に基づく教育は見かけないだけでなく,なぜ採用されないかを答えるための手がかりも,文献を通じて知ることができている.
なお本稿の2~4節の内容はおおむね[Link 20111115][Link 20210907]で公開済みである.
2. 《倍の乗法》と《積の乗法》
小学校の算数の,かけ算の式を立てて求める文章題では,被乗数とかけ算の結果が同種の数量となる事例を多く見かける.
これは国内の算数のローカルルールというわけではなく,初等教育の算数を通じて,かけ算やわり算に関して学習者(児童)は何ができるようになるか,という問題意識を持ち,国内外の文章題の事例を調査していくことで確認できる.
海外文献でよく知られた分類を先に紹介し,その後,日本の算数の状況と照合することにする.[Greer 1992]の分類表には,10個の種別(class)が見られる.そのうち最初の7つ(equal groups:同等のグループ, equal measures:同等の量, rate:単位量あたり, measure conversion:単位の変換, multiplicative comparison:乗法的な比較, part/whole:部分と全体, multiplicative change:乗法的な変化)は,被乗数とかけ算の結果が同種の数量である.いずれも「1つ分の数のいくつ分」または「基準量の何倍」で表現できる.これらの文章題の和訳およびかけ算の式については[Link 20190910]で整理している.
ただし,[Greer 1992]では被乗数と乗数の順序を規定していない.またrateでは,被乗数に当たるものはパー書きの量(例えば4.2m/s)ではない量(例えば4.2m)とする.教科書[学校図書2019]の「速さは,単位時間あたりに進む道のりで表します。」において,数直線(比例数直線または二重数直線などとも呼ばれる)による図示を通じて視覚化される.
以下ではかけ算の結果を「積」と表記し,被乗数と積が同種の数量となるかけ算を,《倍の乗法》とする.乗数は,文章題などにおいて被乗数や積と異なる種類の量となることが多い.例えば[Greer 1992]では,"3 children each have 4 oranges. How many oranges do they have altogether?"(3人の子どもが4つずつクッキーを持っている.全部合わせるとクッキーは何個か)という,equal groupsの文章題を,子どもが最初にかけ算を用いる場面として示している.この文章題を,日本の算数の出題として,かけ算の式で表すと,「4×3」となるが,「3人」が,かけ算においては「3倍」に置き換わって,「×3」として作用することになる.被乗数と乗数の役割が異なるため,「積÷被乗数=乗数」(包含除)と「積÷乗数=被乗数」(等分除)が区別されることも,[Greer 1992]で指摘されている.
《倍の乗法》に相対するものは《積の乗法》である.[Greer 1992]の分類表のうしろの3つ(Cartesian product:直積, rectangular area:長方形の面積, product of measures:量の積)が該当する.これらに共通する乗法の式は「因数×因数=積」である.したがって除法の式は「積÷因数=因数」しかない.
《積の乗法》の3つの種別では取り得る数量に違いがある.まず,Cartesian productは2つの因数と積がいずれも分離量である.次に,rectangular areaは,2つの因数が同じ種類の量(長さ)で積はそれらと異なる量(面積)である.最後に,product of measuresは,2つの因数と積がいずれも異なる量である.量の積の場面において,2つの因数は一般に異なる量であるが,除法は,「積÷一つの因数=他の因数」と捉えることにすれば,1通りのみとなる.
日本の算数の教科書を見る限り,《倍の乗法》のほうが,《積の乗法》よりも多く出題されている.第2学年では,equal groupsの場面が図や文になっており,倍概念の学習ではequal measuresで被乗数・乗数とも整数の場面や,おはじきの長方形的な並び(アレイ[Link 20151229])や日常風景を活用したCartesian productの場面も見られる.タイの研究者らによる分析[Boonlerts 2013][Link 20180902]によると,日本はタイやシンガポールと比較して,より広範な種別のかけ算を導入時から学習している.
[文部科学省2018]の第2学年の数学的活動で例示された団子の数は,equal groupsに,また掲示物の写真の事例は,Cartesian productに対応する.[日野教委2021]で委員が述べた「靴箱の数」も,Cartesian productと推定できる.筆者が大学教育として携わる中では[Link 20211012],ペアとなって動作するプログラムを5つのプログラミング言語で作成したとき,プログラムの総数(2×5でも5×2でもよい)や動作の組み合わせの数(5×5)はCartesian productの事例となるのに対し,写経型学習(プログラムの模写を通じた学習)において「毎日2つずつ,5日間写経する(2×5)」や「毎日5つずつ,2日間写経する(5×2)」はequal groupsに該当する.
第3学年ではmultiplicative comparisonも加わる(例えば3倍して2倍すると,5倍ではなく,6倍となることも学ぶ).第4学年では「小数×整数」の学習においてequal measuresが用いられるほか,multiplicative change(ゴムの伸び)や,rectangular areaも,この学年での学習となる.第5学年で,倍の7種別が出揃う.rateは人口密度や速さといった「単位量当たりの大きさ」であり,part/wholeは「百分率」が密接に関係する.第6学年の「角柱及び円柱の体積」で導かれる公式(底面積×高さ=体積)は,product of measuresである.なお[Greer 1992]の表で例示されているワット×時間=ワット時の場面は,算数の教科書では見かけない.
[岸本2000]では,第5学年児童の小数の乗法の単元について実験授業を行い,事前・事後調査を通して児童の学習状態(演算処理と演算決定のそれぞれについて,できるようになったか)を評価している.この文献では「倍(multiple)に関する小数の乗法を考察の対象とし,積(product)に関する小数の乗法は取り上げない」を明記している.
純粋な数の乗法は,《倍の乗法》にも《積の乗法》にもなり得る.中学1年で学ぶ「負数の乗法」[小林2010]に関して,例えば「負の数×負の数=正の数」を,数直線や,速さなどの物理的モデルを用いて説明する際には,《倍の乗法》に基づく.それに対し数学的公理を用いた証明は,《積の乗法》と関連づけることができる.
3. アレイの認識
ツイッター上で,アレイを提示してa×bとb×aが同じであることを示す発言(ツイート)をよく見かける[Link 20211222].場面とアレイとかけ算の式に関して,筆者は以下のようにQ&Aを作成している[Link 20181115].
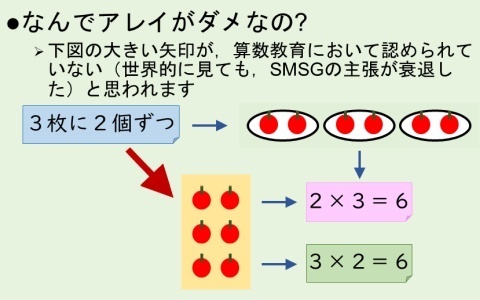
この図の見方を説明する.「さらが 3まい あります。1さらに りんごを 2こずつ のせます。りんごは ぜんぶで 何こ あるでしょう」という文章題から,数量の関係を取り出すと,「3枚に2個ずつ」と表せる.これは図の右上のように,皿に見立てた楕円形の上に,りんごを表した物体が「1さらに2こずつ」で,皿は「3まい」ある状態となる.前節で述べた種別のうちequal groupsが該当する.「1つ分の数×いくつ分=ぜんぶの数」に当てはめて,2×3=6の式で「こたえ 6こ」が求められる.
図の下段中央の,3行2列のりんごの並びから,話を始めると,これはCartesian productとして捉えることとなり,「1つ分の数×いくつ分=ぜんぶの数」に適用すると,2×3=6も,3×2=6も,認められる.
このとき,「3枚に2個ずつ」という数量の関係と,3行2列のりんごの並びとを,対応づけてよいのかという問題が生じる.[Link 20211222]で取り上げた各ツイートはこの点に無頓着に見える.上の図に書いた回答文のとおり,アレイで表現または認識することは,日本の算数において,教科書や授業例などで目にすることがない.ある教科書[教育出版2014]には,「1本に4こずつ入ったボールが3本あります。ボールはぜんぶで何こあるでしょうか。」という文章題に対してアレイ図が載っているが,文章題に対する認識ではなく,4×3と式を立てた上で,4×3=12と計算する際に用いられている.
回答で括弧書きとした「世界的に見ても,SMSGの主張が衰退した」について,SMSG (School Mathematics Study Group)は米国にかつて存在していた団体[Link SMSG]であり,その出版物については,例えば[SMSG 1962]より知ることができる.ただし,数量の関係を3行2列のアレイに図示して「3×2にも2×3にもなる」といった主張は,見当たらなかった.近年では,アレイ図で,縦と横を区別するというテスト事例が提示されている.[Link imgur]より見ることのできる画像は,4×6をアレイで図示せよという問題に対し,短い縦棒を6行4列に並べるのは不正解,4行6列に並べるのが正解とされている.
「3×2にも2×3にもなる」のように主張しているのは,「かけ算の順序強制」などの表記で,現在の日本の算数の教え方・学び方を批判する人々である.例えば[Link Kuroki]では,「犬の足を3×4の長方形型に並べて描いた模式図」を思い浮かべることで,「どちらが一つ分の数であるかを確定させることなく、正しい考え方で正しい答を出すことができます」と主張している.
遠山啓も1970年代に同様の主張を行っている.科学朝日1972年5月号に「6×4,4×6論争にひそむ意味」と題する文章を寄せ,[遠山1978]で読むことができる中に,「教室の机は1列に6つずつ4列ならんでいます.机はみんなでいくつありますか」という問題を例示し,「4×6でも,6×4でもいいとせざるをえないだろう」と続けている.
この机の数の問題について,「1列に6つずつ4列」という表記により,かけられる数(1つ分の数,1あたり)・かける数(いくつ分)が指定されていると解釈できる.[向山2004]では,「こしかけを ならべています。1れつに4こずつ 5れつ ならべると,ぜんぶでなんこになりますか。」という出題が,挿絵とともにあり,正解となる式は「4×5=20」のみとなっている.
米国Common Core State Standardsにも,アレイの場面が見られる.[Link CommonCoreMath]の表のうち,「ARRAYS, AREA」の行,「UNKNOWN PRODUCT」の列のマスに書かれた最初の問いは,"There are 3 rows of apples with 6 apples in each row. How many apples are there?"([高橋2012]の和訳は,「6個ずつ3れつにならんだリンゴがあります。」)である.ここでは1つ分の数にあたる「6」といくつ分にあたる「3」が区別できるよう書かれている.表の脚注1では,"The apples in the grocery window are in 3 rows and 6 columns. How many apples are in there?"という問いにすると"harder form"(より難しい)と指摘されている.
4. 《積指向》とその課題
アレイやCartesian productに基づく教え方・学び方については,日本・フランス・中国で課題が指摘されている.日本は,遠山啓による1979年の講演である[遠山2009].「タイル×タイル」が「子どもにはなかなかわからない」ことや,「外延量×外延量」は一般性を持たず非常に特殊であることを述べ,「総量=内包量×容量という考えに変えた」としている.
フランスでは[Vergnaud 1983],直積が小学校の第2~3学年のかけ算導入によく使われてきたが,そこで多くの児童が,かけ算の理解に失敗していることを,「量の積」「複比例」と関連づけて説明している.中国に関しては,理数教科書に関する国際比較調査結果報告[教育政策研究所2009]で「被乗数と乗数の区別をなくし,最初から因数として扱うこととした」と述べ,「量の扱いではやはり不具合があって,教師たちの丁寧な対応によって乗り越えているところである」として教育過程の課題も指摘している.
ここでかけ算について,「対象(場面)」と「手段(教え方,認識の仕方)」に注意して以下のように分類する.
- 《倍の乗法》:被乗数と乗数が区別され,「b×a」と書くと,「a×b」とは式の意味が異なるとされるかけ算のこと.
- 《積の乗法》:被乗数と乗数の区別は本質的ではなく,「b×a」と書いても,「a×b」と同じ場面や対象を表していると解釈できるようなかけ算のこと.
- 《倍指向》:《倍の乗法》に基づいて,乗法を意味づけるべきだという考え方.もしくは,かけ算で表すことのできるどんな場面や対象も,《倍の乗法》に帰着できるという考え方.
- 《積指向》:《積の乗法》に基づいて,乗法を意味づけるべきだという考え方.もしくは,かけ算で表すことのできるどんな場面や対象も,《積の乗法》に帰着できるという考え方.
[Link 20211222]で取り上げた各ツイートは《積指向》と見なせるのに対し,前節のQ&Aの画像は,《倍指向》である(「3枚に2個ずつ」やその図示は《倍の乗法》,3行2列のりんごの並びは《積の乗法》となる).
《積指向》では,前述した日本・フランス・中国の課題の解決が難しいことについて,その要因を検討する.《積指向》の背景にあるのは,2つの因数が独立して動くことと言える.それよりも,被乗数と乗数の役割の違いに注意して,かけ算の構造を認識することが,「現代化」衰退と合わせて,受け入れられてきた.また,素朴な《積指向》は,Cartesian productに基づいており,2つの因数と積の量の種類が除外されてしまっている.これにより,a×b=xで表される関係のa,b,xがさまざまな種類の量をとることへの考慮が困難となる.3つのうちの一つが未知数で,それをかけ算またはわり算で求められること(演算決定)の根拠が得られにくい.
純粋な数の計算に限っても,[中島1968]では,米国の1960年代の論争を紹介する中で,アレイではや(-3)×(-4)の説明ができないことを述べている.
《倍指向》は,《倍の乗法》にも《積の乗法》にも対応(立式の根拠を説明)可能となっている.Cartesian productの典型例であるアレイに対しては,「一つ分が明示的でない場合に,自分で一つ分を設定」[布川2010]する.しばしば,図で提示された一つの場面に対して,総数を求めるかけ算の式は複数が認められる.それも被乗数と乗数を交換した式の2通りだけでなく,[筑波2012]のかけ算の導入授業では,3行4列の丸の並びに対して,「3こずつ4つ分」「4こずつ3つ分」のほか,「6こずつ2つ分」や「2こずつ6つぶん」も認めている.
アレイに対するかけ算をもとに,長方形の面積では,まず縦も横も単位長の整数倍の場合を考え,単位正方形の「縦の数×横の数」個分の面積により,縦×横の公式化を行い,横×縦でもよいとする.小数を含む長さの場合の面積は,縦または横の一方を固定し,面積は他方の長さに比例することを活用する.柱体の体積については,底面が簡単な場合(正方形・長方形またはその組み合わせ)から算出を行い,高さが単位長の柱体の何倍かを考えることで,底面積×高さへと一般化できる.累加でかけ算を定義したのち,長方形の面積(量の積)や速さ(量の商)への対応や,負の数や無理数を含むかけ算への拡張の仕方については,[田村1978]で読むことができる.
児童らが《積指向》で認識している可能性と,それに対する教師らの反応について,事例を挙げる.[Mulligan 1992][Mulligan 1998]における,かけ算・わり算を学習する児童の方略において,アレイや直積は見当たらない.[浅田2006]では7×2.4の意味から1つを選ぶ設問において,6つの選択肢のうち「長方形の求積」が42.3%を占め最も多い解答となっている(もし,この解答をすべて《積指向》と解釈するなら,他の選択肢のうち3つを《倍指向》と見なすことができ,その合計は50.5%で上回っている).この結果に対し「児童は演算の意味を考えず形式的に問題を解く傾向があるのではないかと考えられる」と評している.[Lannin 2013]でかけ算の作問課題に対し"a superficial knowledge"と述べている事例や,答えは同じと主張する生徒に対して先生が"are you saying that those two number sentences can't be used to describe two different situations?"と問う授業[Chapin 2009]と,関連づけて検討できるように思われる.
5. おわりに
本稿では,「倍」と相対する「積」に基づく乗法の捉え方に関して,《倍の乗法》《積の乗法》《積指向》《倍指向》に分類して出題・学習・認識の状況を整理した.これらのラベリングを用いることなく,かけ算の学習を俯瞰したものを,[Link 20211031]より引用する.
教科書・学習指導案・授業事例を総合すると,かけ算の式について,(国内の小学校の)算数の2~3年で学ぶのは,以下のとおりとなります。
- かけ算の式を,言葉を使って表すと,「1つ分の数×いくつ分=ぜんぶの数」です。
- 倍の場面では,そこから1つ分の数といくつ分を特定し,かけ算の式に表したり,その逆を行います。
- 倍の場面では,かけられる数とかける数を反対にした2つの式(2×3と3×2など)が,異なる場面を表すことも学びます。
- 積の場面では,そこから1つ分の数といくつ分のペアを自分で決めて,かけ算の式に表したり,他の児童が表したかけ算の式の読み取りを行います。
筆者の現在の関心は,第2学年と第5学年(乗法の意味の拡張[中島1968][岸本2000])の間の学年におけるかけ算の学習(授業・テストを含む)である.ここでは2例を挙げておく.一つは,第3学年の結合法則の学習で出現する「1こ50円のドーナツが,1箱に4こずつ入っています。2箱では,何円になるでしょうか。」[教育出版2019][Link 20220121]に含まれるかけ算である.50×4=200の式で,「1個あたりの金額」と「1箱あたりの個数」の積により,「1箱あたりの金額」が得られ,[Greer 1992]の種別のproduct of measuresが第3学年で出現することになる([Schwartz 1988]のI×I'=I''の事例でもある).もう一つは,[文部科学省2018]の第4学年の数学的活動で記載された「段数×4=周りの長さ」(2年で学ぶ「1つ分の数×いくつ分=ぜんぶの数」に合わない)に関する学習[Link 20190617]であり,[筑波算数2022]でも授業例が紹介されている.