準備
「a×b」という,かけ算(乗法)の式を前提とします.ここでaを被乗数,bを乗数と呼びます.実際には,aとbにはそれぞれ,整数,小数または分数が入ります.
- 被乗数と乗数が区別され,「b×a」と書くと,「a×b」とは式の意味が異なるとされるかけ算を,《倍の乗法》と呼びます.
- 被乗数と乗数の区別は本質的ではなく,「b×a」と書いても,「a×b」と同じ場面や対象を表していると解釈できるようなかけ算を,《積の乗法》と呼びます.
- 《倍の乗法》に基づいて,乗法を意味づけるべきだという考え方を,《倍指向》と呼びます.
- 《積の乗法》に基づいて,乗法を意味づけるべきだという考え方を,《積指向》と呼びます.
これらの命名・分類はtakehikom個人によるものです.ただし,[Greer 1992]に大きく依拠しています.今月13日に書きました.
《倍の乗法》の出題例として,「3人の子どもが4つずつミカンを持っている.全部合わせると何個になるか?」や「あるゴムバンドは,元の長さの3.3倍まで伸ばすことができる.元の長さが4.2メートルのとき,完全に伸ばしたら何メートルになるか?」が挙げられます.《積の乗法》の出題例には,「縦3.3メートル,横4.2メートルの長方形の面積はいくらか?」や「4人の男の子と3人の女の子がダンスをするとき,男女のペアは何通りできるか?」があります.
《倍指向》と《積指向》は,別の言葉で定義することもできます.
- 《倍指向》とは,かけ算で表すことのできるどんな場面や対象も,《倍の乗法》に帰着できるという考え方のことです.
- 《積指向》とは,かけ算で表すことのできるどんな場面や対象も,《積の乗法》に帰着できるという考え方のことです.
雑多な補足です.2つの数のかけ算で表せる場面・出題のみを対象とします.「式の意味」とは「書かれた式が何を表すか」であり,「なぜその演算を使用して式を書くのか」を含む「演算の意味」とは別と考えます.
《倍指向》と《積指向》の具体例
《倍指向》と《積指向》を特徴づけるもの,すなわち「これが《倍指向》・《積指向》だ」というものが何になるかは,今のところ模索中です.
なのですが,「これは《倍指向》・《積指向》の傾向と言っていいだろう」というものは,いくつか分かっています.
《倍指向》には,累加(同数累加)と,比の3用法(割合の3用法)が挙げられます.累加により,3×5=3+3+3+3+3,5×3=5+5+5と表されます.3用法の中で第2用法がかけ算の形,例えばA=B×pとして表されますが,慣例としてbaseになる数は×の左に,proportionになる数は右に書きます.
《積指向》としては,離散的にはデカルト積(直積),連続的には面積を利用するものが挙げられます.トランプ配りの乗法への適用*1も,ここに入ります.
わり算からも,《倍指向》と《積指向》を見ることができます.a×□=cの□を求めるのが包含除,□×b=cの□を求めるのが等分除,として区別するのは,《倍指向》です.それに対し,等分除は包含除に帰着されるという考え方は,すべてがそうとは言えませんが,《積指向》の傾向を持っています.
数学教育協議会(数教協)の指導法で顕著な,内包量×外延量=全体量と,かけわり図が,それぞれどちらに属するかについては,今のところ保留します.
2×2
《倍の乗法》と《積の乗法》,《倍指向》と《積指向》とを組み合わせると,次のようになります.
- 《倍指向》で,《倍の乗法》の問題を解くとき,正解となるかけ算の式は1通りだけです.
- 《倍指向》で,《積の乗法》の問題を解くとき,正解となるかけ算の式は2通りあります.
- 《積指向》で,《積の乗法》の問題を解くとき,正解となるかけ算の式は2通りあります.
- 《積指向》で,《倍の乗法》の問題を解くとき,正解となるかけ算の式は2通りあります.
このうち,「《倍指向》で《倍の乗法》」と「《積指向》で《積の乗法》」は,それぞれ定義から明らかです.
「《積指向》で《倍の乗法》」の典型例はいわゆるトランプ配りで,後述します.
「《倍指向》で《積の乗法》」は,長方形の面積を求める際に現れます.なお,「縦×横」のみを正解とし「横×縦」は間違いとするという事例を,主にWeb上の掲示板やブログのコメントで見かけますが,教科書・問題集・学習指導案・学力テストで文書化されたものに関してこれを見たことはなく*2,書店で目にしたいくつかの本では両方を認めています.
《倍指向》の世界観
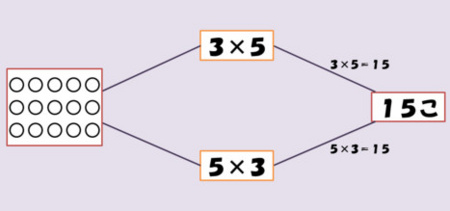
「3×5=15と5×3=15を,何が同じで何が違うかが分かるように,一つの図で表してください」と,《倍指向》の人にお願いすると,こんな図を描いてくれそうです.

図や式,結果となる値を結びつけるのは,矢印(有向辺)です.ある実体から逆の実体へは移行しますが,その逆には行けません.両向きの矢印は,対立ではなく,双方向に行き来が可能な関係を表します.式から図に行くことができるのは,算数的活動で重視されている,式を読み取ることを反映しています.
《積指向》の世界観
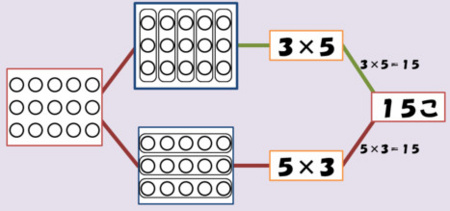
「3×5=15と5×3=15を,何が同じで何が違うかが分かるように,一つの図で表してください」と,《積指向》の人にお願いすると,こんな図になります.
関連する対象同士を結びつけるのは,線分(無向辺)です.上で書いた両向きの矢印と同じく,どの方向にも自由に行き来ができる関係です.
世界観を合わせる
上の2つの図について,すり合わせを試みます.なるべく合わせて,違いを浮き彫りにします.《倍指向》の世界観の修正版は次のとおり.

そして《積指向》の世界観の修正版は,こうなります.

こうして見比べてみると,《倍指向》は,各状態(知識,図など)の関係性を重視するものであり,知識を増やそうとする考え方に見えます.
それに対して《積指向》は,先ほど「自由に行き来ができる」と書いたことと合わせ,最初から全体を知り得る立場のようです.
なお,これらの図は「思考展開図」となります.畑村洋太郎氏らが提案する図式で,左端に一つの状態・情報があり*3,左半分でどんどん展開させ,右半分では収束・集約させながら,最終的に結論となる一つの状態・情報に至ります.思考展開図に関する1冊の本と,人工知能学会に掲載された一つの論文をもとに,ここからは私個人の活動になりますが,プログラムコードの表現や読解支援に応用できないかと考え,この図式をclamshell diagramと命名し,2008年から今年まで,学会発表する機会を得ました.
《倍指向》で例の問い
すり合わせた世界観をもとに,「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう」という問題がどのようになるかを見ていくことにします.《倍指向》だと,いくつかの要素を取り除いて,次の図になります.

太線で囲った状態を起点に,立式し,答え(個数)を求めるという流れです.
このとき,「5×3」という式や,それに対応する配置と囲い込みは,消失します.もし図の中に残すとするなら,それは,いったん「5×3」という式を書いたけれども,この式の表す状況を(紙に,もしくは頭の中で)表してみると,問題文が表しているものと違うことに気づく,といった使い方になりそうです.
《積指向》で例の問い
「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう」は,《積指向》だとどうなるでしょうか.

ここも,《倍指向》での答え方と同じく,太線で囲った状態を起点とします.すなわち《積指向》であっても,3個を「一つ分の大きさ」として,それが5つあることは,問題文から読み取っているものとします.
次にするステップは,3個を「一つ分の大きさ」とする囲い込みを取り除くこと,すなわち図の左端の状態に移動することです.こうすると《積の乗法》となり,「3×5」も「5×3」もそれを表す式となります.
この解き方では,「3個が5つ」と「5個が3つ」のグループ化は,必要としません.《積指向》では左端の長方形的配列を起点にして問題を解く,と言うこともできます.
また別の図示の仕方を紹介します.すり合わせた《積指向》の世界観からの変更が,上図よりも少なめです.
この図にある,「5個が3つ」の配置は,《積指向》を支持する人々が,《倍指向》の方法論によっても2種類の式が得られることを示すための中間的なステップと言えます.赤の太線の経路,すなわち「3個が5つ」を起点として「5個が3つ」に変換する作業は,トランプ配りという名称で知られています.
《積の乗法》を《倍の乗法》で
《倍指向》と《積指向》の別解釈を,再掲します.
- 《倍指向》とは,かけ算で表すことのできるどんな場面や対象も,《倍の乗法》に帰着できるという考え方のことです.
- 《積指向》とは,かけ算で表すことのできるどんな場面や対象も,《積の乗法》に帰着できるという考え方のことです.
ここで,
- かけ算で表すことのできるどんな場面や対象も,《倍の乗法》に帰着できるのか?
- かけ算で表すことのできるどんな場面や対象も,《積の乗法》に帰着できるのか?
という疑問が生まれます.どちらも肯定的に示せそうで,それぞれラフスケッチを描くことにします*4.
前者は,《積の乗法》が《倍の乗法》に帰着できれば十分です.小学校の算数で典型的な《積の乗法》は,それぞれ次のようになります.
- いわゆるアレイ図におけるドットの計数については,「1つ分の大きさ」と「幾つ分」を見つけるよう,囲い込みをします.その囲い込み方に応じて,《倍の乗法》で式が定まります.囲い込み方は,上の世界観の図のように*5少なくとも2種類あります.そして交換可能な2種類の式が,ともにドットの総数を求めるための式となります.
- 長方形の面積について,まずは,単位正方形の個数を数えます.この個数の数え方は,アレイ図と同様です(したがって,《倍の乗法》に帰着されます).結局のところ,面積=縦×横,面積=横×縦の2種類の式が得られます.*6.
- デカルト積(または直積)に関して,まず,場合の数の積の法則は小学校で指導しない点は指摘しておかないといけません.それでも,場面・対象に応じて,「一つ分の大きさ」と「幾つ分」を見つけることは可能で,それにより,《倍の乗法》に基づく式を得ます.
- [Greer 1992]にある,電力量計算(一般には,2つの量の積)については,単位正方形と同様に「1キロワットの電力を1時間で消費する量」すなわち「1キロワット時」を,積の単位量とし,2種類の比例関係から,求めることになるでしょう.ここで(一つの)比例関係の式すなわちy=k×xは,《倍の乗法》で解釈することになります.2種類の比例関係(「電力が固定なら,電力量は時間に比例」と「時間が固定なら,電力量は電力に比例」)のどちらを先に適用するかによって,2通りのかけ算の式が得られます.
アレイ図と長方形の面積は,「小学校学習指導要領解説 算数編」(《算数解説》)で読むことができます.*7
《倍の乗法》を《積の乗法》で
次に,上の反対,すなわち《倍の乗法》を《積の乗法》に帰着することを試みます.
- 整数の乗法は,アレイ図で表します.
- 小数や分数を含む場合は,複比例の関係y=a×bまたはy=k×a×b(yはaに比例する.yはbに比例する.aとbは独立である)で表します.
「鉄の重さは銅の0.88倍である.ある銅のかたまりが4.2kgのとき,それと同じ大きさの鉄のかたまりは何kgか?」という,一見,0.88のみが倍率としか見なせない状況でも,「物質Xの重さは銅のa倍である.ある銅のかたまりがb kgのとき,それと同じ大きさの物質Xのかたまりは何kgか?」と一般化すれば,求めるべき重量yは,aにもbにも比例するので,y=a×b=b×aと表せます.
このように帰着はできますが,学校教育では(とくに日本では,知る限り)この方針ではありません.整数の乗法に関しても,「アレイ図の問題も数えられる」であって「アレイ図に表して数える」ではありません.
数学的には?
すべて《倍指向》というのは言い過ぎにしても,倍概念に基づく検討が多く見られます.
高木貞治『新式算術講義』pp.213-246では,(一つの)量の空間を基に,それに属する量どうしの比として実数を導いています.南雲道夫(Quantities and real numbers, 1977)は,1つの量の集合Qに対して,QからQへの線形写像(自己同型写像)を定めると,その写像Φは倍率mと対応づけられることを示しています.田村二郎『量と数の理論』は,南雲の論文を継承しつつ,面積や速さといった,2つの量から得られる量についても検討しています.
田村の書籍で参考文献に挙げられている,小島順『線型代数』では,p.48に「普通の感覚で積(掛け算)と呼ばれるものが双線型写像に他ならない」とあります.しかしそれより前のページでは,速度や密度を,2つの量の線型写像(の一つ)を(一つの)量に対応づけて,積の関係が成立することを確認しています.その記載と,算数教育を結びつけるなら,量の対応づけ作業は比の第1用法,積の関係は比の第2用法となります.
教育面では?
教育現場では圧倒的に《倍指向》と言っていいでしょう.「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう」の問題に,「5×3=15も正解とすべきだ」とする算数教育の専門家が皆無であることを,根拠の一つとして挙げることができます.
海外の文献を見ても,[Greer 1992]では《倍の乗法》が先,《積の乗法》は後に説明されています.また[中島1968b]は,「乗法は累加である」を主張するRappaportの記事について,次のように解説しています.
ア.乗法を累加として教えるといっても,全ての数学の乗法をその考えで説明するのではない.新しい数が導入されるときには新しい定義が一般に必要であり,再定義されるべきものであること.
(略)
結論として,こどもは,具体的な経験をもち,それを一般的化していくのであって,最初の学年水準での一般化は,必ずしも,数学者の論理性に合致する必要は無い.累加がこどもにとって意味があるかぎり,教育的に健全であり,この解釈を用いることは,論理的にも健全である.
しかし,解釈は排他的であってはならない.こどもには,アレイも集合の直積も学習させてよいが,だいじなことは,こどもに学問のしかたを教えることであって,学問からはじめることを主張すべきではない.
なお,《積指向》に関して,アレイ図やデカルト積(直積)をもとに整数の乗法を意味づけることは,数学教育の現代化と密接な関係があり,その試みは米国で(そして日本でも)失敗に終わり大幅な修正を余儀なくされたと理解しています.
最初は《倍指向》で意味づけを行い,ある程度の段階で,例えば長方形の面積の公式や乗法の交換法則を学習すれば,あとは式にする際に被乗数と乗数の区別に執着しないという考え方もあります.今年出た書籍で,該当する記述を9月28日に引用しています.[中島1968a]および[中島1968b]では,複比例の考え方の重要性を説いています.
まとめ
「倍か積か?」という問いを立てるなら,「記述能力としては同等」という確信を持っています.あくまで略証でしたが,次の2つが言えます.
- 《積の乗法》を《倍指向》で(《倍の乗法》に帰着させて)式に表すことができます.
- 《倍の乗法》を《積指向》で(《積の乗法》に帰着させて)式に表すことができます.
したがって,数学的・論理的には,どちら指向でもよいのです.
そのもとで,学校教育の実情を見ていくと,《倍指向》であると言わざるを得ません.アレイ図で,個数を数える式を立てるにも,「一つ分の大きさ」と「幾つ分」を意識しています.そのおかげで,4行6列に並んだ状態に対して,「4×6」「6×4」のほか,「3×8」を得ることも可能となります*8.
《倍の乗法》を《倍指向》で解くので,式は1種類が定まり,そこから被乗数と乗数を交換した式は誤答となります.トランプ配りに関しては,囲い込みを取り除く操作が不自然・不適切と言えます.
本日は,(1)乗法の交換法則を理由として,被乗数・乗数をどちらにしてもよいという主張,(2)累加への対案として,内包量×外延量=全体量とする乗法の意味づけ,については検討していません.ともに今月16日に書いていますので,関心のある方はどうぞ.
当日夜に,「《積指向》で例の問い」の画像を差し替えたほか,本文にかなり手を加えました.
*1:トランプ配りは等分除を説明する際にも用いられますが,ここでは除外します.
*2:「《倍指向》で《倍の乗法》」に関しては多数の事例があります.http://d.hatena.ne.jp/takehikom/20110723/1311351165をご覧ください.
*3:この制約を設けなければ,15個の丸が様々に(ランダムに)ある無数の状態,5行3列に配置された状態,そしてそれらの状態および今回の図の左端の状態(3行5列に配置された状態)の間での遷移関係も,世界観の図に加えるべきかもしれません.
*4:厳密に検証するなら,まず,用語や概念の定義を明確にしないといけません.例えば,「帰着」とは何か,そもそも乗法は《積の乗法》と《倍の乗法》に分割できるのか(両者に属さない,乗法の場面はないのか)などをクリアする必要もあります.
*5:図の左端を起点として,式をつくるという問題になります.指導事例や問題集で数多く見られます.
*6:正方形,三角形,平行四辺形の面積の公式は,長方形の面積の公式をもとに導出します.円の面積の公式は,平行四辺形の面積の求め方と,極限によります.
*7:アレイ図は,本文中にその名称はありませんが,第2学年のp.81で,「12個のおはじきを工夫して並べる」件です.長方形の面積は,第4学年のp.147です.
*8:《積指向》では,並べ替えをしないと,得られないように見えます.どちらが,数についての感覚をより豊かにしてくれるでしょうか?