おことわり:「答えは同じだけど,意味は違う」を取り上げた記事の最新版は,3×4と4×3,答えは同じだけど,意味は違う(令和2年版) - かけ算の順序の昔話です.
- https://twitter.com/akisameruu/status/428812052841250816(デッドリンク)
- [B! 掛け算] http://twitter.com/akisameruu/status/428812052841250816
たった2日で,多数のはてブ.[twitter:@akisameruu]さんをフォローすることにしまして,その後のツイートを見ました.おつかれさまという思いに加え,自分としては適切な形のリファレンスを,タイムリーに提供できるようにしておかないと,という思いを新たにしました.
画像を見て,一つ,思い浮かんだのは,ツイートでリンクしている,2×3と3×2の違いを表したという絵を,かけ算を学習中の小学2年生の子どもが描いたとしたら,自分は,みんな(大人)は,クラスの子どもたちは,どのように反応するのだろうか,です.
「違いがよくわかるね」でしょうか,「2×3の絵,3×2じゃないかな」でしょうか.
どのくらいのパーセンテージでそれぞれの(または他の)反応をするか,またそれは小学校の先生とそうではない人々とで違ってくるのか,断言はできません.
しかしながら,はてブのコメントを見たところでは,「2×3の絵,3×2じゃないかな」や,そこから派生し「2×3の絵は,3×2でもある」「3×2の絵は,2×3でもある」を経て,「どちらも2×3であり,3×2」と読めるものが,「違いがよくわかるね」より確実に多いと言ってよさそうです.
ちなみに私ならどう反応するか,メモしておきます.我が子が将来,そのような本人なりに描き分けたものを持ってきたら,「ふむ,こう描いてみたんやな」と反応し,後はケースバイケースでしょうね.学校の先生がこれをバツにしたというのなら,その2×3の絵を3×2(=3+3)と見られちゃったんだね,と言うことになります.
本題に進む前に,自分のスタンスを書いておきます.これまで見聞きしてきた情報をもとに,かけ算の順序の件は,次のとおり認識するようになりました.
- 文字のみだと,「2×3は[●●][●●][●●],3×2は[●●●][●●●]」が最も簡潔です.*1
- 「2×3で求められる」と「2×3で表される」を区別します.*2
- 「[●●][●●][●●]は,2×3だけでなく,3×2でもあるのだ」といった主張には,賛同できません.その考え方を認めると,「[●●][●●][●●]と[●●●][●●●]は算数において区別できない」が推論できます.*3
さて,これまで書かれてきた情報(教師の経験が文字や絵になったもの)と,照らし合わせていくとします.新たなリファレンスづくりを兼ねています.
a×bとb×aの,図示による違いの表現は,2012年,2011年,そして1961年にそれぞれ出版された本に載っています.
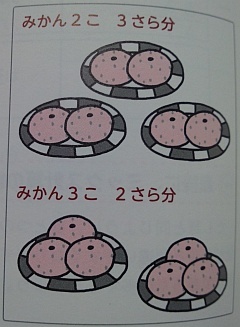


本は,上から順番に,次のとおりです.
- 東京書籍(2年下p.21)*4
- えんぴつを 1人に 2本ずつ,5人に くばります。えんぴつは,ぜんぶで 何本 いりますか。
- えんぴつを 2人に 5本ずつ くばります。えんぴつは,ぜんぶで 何本 いりますか。
- 大日本図書(2年下p.45)*5
- 2つの ふでばこに えんぴつが 6本ずつ 入って います。えんぴつは 何本 あるでしょう。
- えんぴつを 1人に 2本ずつ,6人に くばります。えんぴつは 何本 いるでしょう。
問題集からだと,昨年出た『算数の学習プリント―学力調査・算数的リテラシーに対応! (教育技術MOOK)』に,6×4,4×6の式を先に与え,それぞれの「式になるようなもんだいをつくりましょう」とする出題があります.
かけ算の式にするより前の段階で,違いを理解するようにしよう,というツイートも見かけます*6.
算数では,どんな場合も,a×bと書いたらそれはb×aではない(b×aと表せない),としているわけではありません.一つの図が,a×bにもb×aにもなるという場面の例もあります.例えば以下の内容をもとに,公開授業が行われています.

番号が「3.」から始まっていますが,まずは,「はこが、4はこあるよ。それぞれのはこには、あめが3こずつ入っているよ。」という文をもとにして(絵は見せずに),子どもたちが式を答えていきます.
「3×4=12」「4×3=12」の式が出て,文と合っているかを話し合います.
その後,絵はこうなのでした,と提示します.
冷静に読めば,その図に対して「はこが、4はこあるよ。それぞれのはこには、あめが3こずつ入っているよ。」は情報不足なのが見てとれます.文からは,どの箱にも□△○が1個ずつ入っているという情報が,含まれていません.そのため,図の提示の前後で,認められるかけ算の式が変わってしまうわけです.*7.
海外に視点を移します.昨年11月,台湾メディアが,自国内の教育の話題として,この種のかけ算の問題を報道しました.
問題文は「一打鉛筆有12枝,毎枝賣8元,一共幾元要如何計算?①8×12②12×8③8+12④12+8。」で,日本語に訳すと「鉛筆1ダースは12本である.鉛筆が1本8元のとき,全部で何元になるかを,どの式で求めればよいか」です.12×8を選んだら,間違いとされています.動画の途中では,老師(先生)がホワイトボードを使って解説しており,「被乘數」「單位」をかけ算の記号の左に,「乘數」「數量」を右に書いています.
ですのでこの台湾の件,日本と同じです.韓国も同様なのを,掲示板を通じて把握しています.冒頭のはてブコメントの中で,id:gimonfu_usrさんがwikipedia:かけ算の順序問題(海外でのかけ算の導入)にリンクしていますが,中国に関しては,授業観察をした秋田大学の杜威教授が,「量の扱いではやはり不具合があって,教師たちの丁寧な対応によって乗り越えているところである」と指摘している(*)ことにも,留意したいところです*8.
もう一つは,1988年に出た洋書からです.主要部は次のとおり.
For children, three lots of four and four lots of three are fundamentally different. They think in concrete terms---three children each having four candies are luckier than four children each having three candies although the total number of candies is the same.
Exercises
1. Give some real-life examples of situations in which a multiplication product a×b (for example, 5×6) is not the same as b×a (6×5).
The balance or symmetry in the multiplication square relates to a very important property called the commutative property of multiplication, which states that for any two numbers a and b, a×b=b×a (for example, 3×4=4×3). Note that this is a property of numbers. While it is true that 3×4 is equal to 4×3, 3×4 may not be the same as 4×3 in a real-life situation.
要約すると,初めの引用は,「3人の子どもたちが4個ずつキャンディを持っている」「4人の子どもたちが3個ずつキャンディを持っている」とでは,キャンディの総数は同じだけれど,4個ずつキャンディを持っている子のほうが,3個ずつの子よりも"luckier"ということで,場面の違いを表しています.2番目の引用は,a×bとb×a,例えば5×6と6×5とで,違いがわかるような日常生活の事例を挙げよという練習問題です*9.最後は,交換法則(commutative property)は純粋な数における性質だよ,日常生活では違ってくるねと注意をしています.
出典は以下の本です.英文をコピーして,検索したら,和訳を含むより詳細な情報も見つかると思います.
この1年,「かけ算の順序」についての新展開も,いくつか見ることができました.上で紹介できなかったものとして,第一に挙げないといけないのは,いくつかの教育委員会の対応でしょう.
- 小学二年生での掛算の指導に関する資料についての京都府教育委員会への問い合わせへの返事が届きました。
- http://togetter.com/li/614514(デッドリンク)
- http://cgi.city.yokohama.jp/shimin/kouchou/search/data/25003016.html(デッドリンク)
かけ算の出題で,印象に残っているのは,以下の画像です.これは東京都算数教育研究会による学力実態調査の1問で,約6万人の2年生が解答しています.前回(2年前)から,問題提示が少し変更されています.
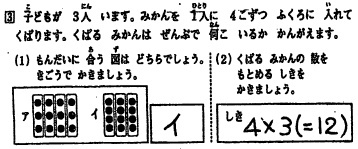
これから1年はというと,平成27年度から使用される小学校の教科書の検定結果が出て,読み比べる機会ができるはずです.読めるところに足を運びたいのですが.
これまで作ったリファレンス
その後のリファレンス
2017年4月より,「かけ算の順序」に関する記事はサブブログ(かけ算の順序の昔話)で扱っております.2017年に公開された新しい学習指導要領や,2020年度からの算数教科書についても,記事を書いています.「答えは同じだけど,意味は違う」を取り上げた記事の最新版は,3×4と4×3,答えは同じだけど,意味は違う(令和2年版)です.
*1:「外国だと…」「単位を付けて書くなら…」といった条件が加われば,それに応じて説明も増やすことになります.
*2:[●●][●●][●●]は,2×3で表されるものなのに対し,[●●][●●][●●]も[●●●][●●●]も,2×3で求められます(後者では少し操作を必要とします).2年の授業やテストでは,(3×2で表したり求めたりするのではなく)「2×3で表す」ことができるよう意図して授業を組み立て,また出題をしています.
*3:この推論結果は,ピンポイントで言うと学習指導要領解説で書かれている「記号×を用いた式の簡潔さや明瞭さを味わうこと」と,また広い目では国内外また歴史的な算術・算数・数学の知見---とくに被乗数と乗数の違いに関して---と,合致しません.
*4:http://ten.tokyo-shoseki.co.jp/text/shou/subject/sansu/tsumazuki/ebook/pdf/2.pdf は現在デッドリンク
*5:http://www.dainippon-tosho.co.jp/h23/sansu/sansulink/sa11/default1.html は現在デッドリンク
*6:これは定期的に流しているものらしく,https://twitter.com/GakkenKyoshitsuを開いて遡っていくと,1月23日や16日にも同一内容のツイートがあります.前後も同じなので,機械的に送っていると思われます.
*7:ある状況まではナニナニだけれど,実はコレコレなんだよという演出は,他にも見たことがあります.ちょうど良い書籍が見当たらなかったので,思い出しながら書くと…封筒を横にし,紙を引き出していきます.どの列にも3個ずつ,○が描かれています.3個の○,3個の○,3個の○,と出たところで,○の数は,3の段のかけ算で求められることを,教室内で共有します.式で表すと,最初の3個が出たときは3×1,次は3×2,それから3×3です.さらに引き出したら,やはり3個の○.なので3×4です.その次に仕掛けがあって,○は2個しかありません.このときは,3の段のかけ算で表すことができません.なのですが,2個ずつで7つあるので,2×7=14として求められます.そしてこれが,学習指導要領解説に書かれている,「一つの数をほかの数の積としてみる」活動になっている,ということでした.
*8:「かけ算の順序はどちらでもいい」を,日本の小学校の算数指導の主流にしようとするなら,それは中国の後追いになるのではないですか,という問題点も投げかけておきます.これに対する個人的な認識は次のとおり:「かけ算の順序はどちらでもいい」は「ネット上の定説」であり,そこには国際面・歴史面・学術面・実践面での検証がなされておらず,学校教育では受け入れにくいだろうなと感じています.
*9:a×b≠b×aや5×6≠6×5を示せ,とは書かれていません.積(かけ算の答え)が同じになるのを前提として,a×bとb×a,5×6と6×5といった,別々のかけ算の式で表される場面を,それまでに学習したかけ算の意味や式の意味に基づいて,作ってみましょうという意図なのが読み取れます.




