ちょうど9か月前のツイートですが,先日,[twitter:@aman_GT]さんに,お気に入り登録をされました.ツイートを経緯とともに読み直したものの,個人的には釈然としない内容ですし,「「横×縦」は不正解にも減点に」の直後に「も」が抜けているなあと思ったりもします.
それで@aman_GTさんのツイートを見たところ,北海道で小学校の先生をなさっていること,教科書や教師用指導書やテスト問題にアクセスできることなどが分かりました.また「基準量が後に示された問題」については,「掛順ひっかけ問題」という名称を用いています.
いろいろな点で当方と,学校について,指導について,学校の外について,認識が異なるのですが,ともあれこうしたご縁ですし,こちらで持っている情報を書き出し,リンクしておくことにします.
文章の後半では,箱囲みで3つのお話が登場します.
- 縦が4m,横が
mの長方形の面積は何m^2でしょう.
- 4m^2の
倍は何m^2でしょう.
- 1dLで4m^2ぬれるペンキがあります.このペンキ
dLでは何m^2ぬれますか.
このうち,子どもたちの反応として「かけられる数とかける数が入れ替わっても大丈夫」としているのは,長方形の面積のみです.2番目(倍,同種の量の割合)と3番目(異種の量の割合)では,そうなっていません.
面積かけ算ツアー
素朴な疑問として,「長方形の面積の公式はなぜ『たて×よこ』なのだろうか」があります.
長方形の面積,数直線でかけ算わり算
そうすると,次の疑問は,「『よこ×たて』でもいいんじゃないか」としたいところ.
なのですが,この論文の最初の2ページを読むと,そうではなく,「英語ではLength×Widthと表せるが,このLengthが『たて』,Widthが『よこ』になるのだろうか」となります.
その疑問の答えは,“否”です.長い方がLength,短い方がWidthです.(略)
- xが,a,bのどちらとも同じ性質ならば,そのa×b=xは「数×数」です.
- xが,a,bのいずれか一方とだけ同じ性質ならば,そのa×b=xは「量×数」です.
- xが,a,bのどちらとも異なる性質ならば,そのa×b=xは「量×量」です.
上のそれぞれに属する例を一つずつ,示します.
積・倍・積〜新たなかけ算のサンドイッチ
- 机の問題:教室の机は1列に6つずつ4列ならんでいます.机はみんなでいくつありますか?
- りんごの問題:さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。
- 長方形の面積:縦3cm,横7cmの長方形の面積を求めなさい.
昨年,「親として,我が子はこうあってほしいと願う権利がある一方で,学校や親の要求に対して自分なりに調整し,その都度「答えを出していく」のは子ども自身である」と書きました.そう思うようになった一節を,抜き出します.
面積図は門前払いもう40年以上も前のことですが,筆者は子どもの算数の教科書を見ると単位をつけていないので,これでは数学ができなくなってしまうと思い,自宅で教えるときは式には単位をつけることを要求しました。上の男の子は私が相手のときは単位をつけ,学校ではつけないと使い分けました。結局両方でマルを貰っていたわけです(これはあとで知ったことです)。一方,下の女の子は頑固に学校の先生の方針に従い,私のいうことは聞こうとはしませんでした。案の定,上の男の子の方が数学の実力はつくようになりました。
その結果はどうなったかというと,ともに東京大学に入学できましたが,男の子は理学部数学科に進学したのに対して,女の子は教養学部教養学科でした(もっともこの女の子も今は高校の数学教師をしていますが)。
編著者2名のプロフィールには,共通して「北海道算数数学教育会」が書かれています.奥書の一つ手前,執筆者一覧では,監修者を除く全員の所属が,「北海道教育大学」または「札幌市立」から始まり,「小学校」を含みます.といったわけで,北海道の算数指導に携わる先生方の間で,本にする価値のある指導内容が取りまとめられた,と思ってよさそうです.
「どっちの式でもいいのかな」は,pp.52-55の4ページです.p.52は文章による解説,p.53は「アイディアシート」による,授業指導のための構図,そしてpp.54-55の見開きで,板書例や指導上の注意が記されています.
その4ページで,コアとなる出題は:3まいのおさらにりんごが6こずつのっています。りんごはぜんぶで何こですか。
これを,「「あれ?」を生む問題」としています.(略)
どっちの式でもいいのかな - 北数教
前者にアクセスすると…6学年4領域の表で,学習指導案のPDFファイルにリンクされています.
北数教の指導集
(略)
ともあれ,北数教の指導集を読んだ限り,3年まで,乗法の意味を重視した指導をしていると,見なしてよさそうです.
ジェットコースター問題,論争になっている問題,学習指導案から思い浮かぶ算数の授業…それらを結び付けて言うなら,「一つの問題(場面)に対し,複数の答え・反応が考えられる」という点でしょう.(略)
4年で「どちらでもいい」を見かけました(p.54).
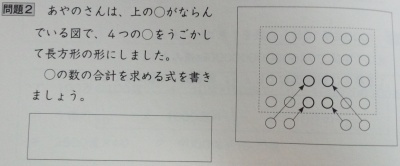
○○○○○○ ○○○○○○ ○○ ○○ ○○ ○○ ○○ ○○という配置があって,○の総数を求めること…が問題ではなく,式が添えられています.4人の子どもたちの式があって,①は10×2+4です.「どのように区切って考えたのでしょう。区切りの線をかきましょう」と出題しています.
算数の学習プリント
それを踏まえて,次の問題です.
長方形配置だから,4×6でも6×4でもいいはず…解答を見ると(p.115),「4×6または6×4」となっていました.
かけ算の意味を定着させるための指導には,かける数を先に書く文章題の他にも方法があり,また英語の文献でも見ることができる.それは,a×bとb×aの違いを学ぶことである.
a×bとb×a
まずは教科書を見ておこう.東京書籍の2011年度版では,「えんぴつを 1人に 2本ずつ,5人に くばります。えんぴつは,ぜんぶで 何本 いりますか。」と「えんぴつを 2人に 5本ずつ くばります。えんぴつは,ぜんぶで 何本 いりますか。」を並べて提示している[Link 14J].いずれも2が先,5が後に出現しているが,状況は異なる.そして順に2×5,5×2と式に表すことが期待される.後者は,かける数が先の文章題でもある.したがって,このペアで式の違いを学習したあと,りんごの問題に「5×3」と書いた児童には,これは「えんぴつを 2人に…」の問題と同じ,と復習することができる.大日本図書による同年度の教科書にも,同様のペアがある[Link 15J].
ここからは海外の文献を見ていく.AnghileriとJohnson [Anghileri 1988]は,4つずつキャンディを持っている3人の子どもたちは,3つずつキャンディを持っている4人の子どもたちよりも幸運であるという例を使って,「4が3つ」と「3が4つ」の違いを説明している.交換法則についても,それは数の性質であり,3×4が4×3と等しいのは事実だが,日常生活においてそれらが同じとは限らないと述べている.
日本は教育先進国であり,教育コンテンツや指導法の輸出国でもある[Link 16J].算数の教科書を東京書籍と啓林館が英訳して販売しており[Link 17J][Yoshida 2009][Link 18J][Link 19J],日本の算数教育に関心のある外国の教師・研究者や,海外在住で将来日本に帰国する児童が活用している.
日本の算数教育の特徴
しかしかけ算の順序を含め,日本の方式をそのまま海外に浸透させようというのではなく,各国の言語や文化に対する配慮も見られる.例えば馬場卓也[馬場2002]は,タイ語のかけ算の自然な語順は日本語と同じであるが,教科書の式は英語と同じという観察から,学習者の認知的な負担を指摘し,他の事例と合わせて,教育の国際協力におけるカリキュラム開発の注意点を提示している.また筑波大学とメキシコ教育省の共同事業によりスペイン語の教師向け指導書が作成され[Isoda 2009],その理論的検討においてxj(xにjを下付き文字で添えた記号)を日本式のかけ算の記号とし使用し,日本語とスペイン語でのかけ算の式の違いを考慮している.
かけ算の文章題で、幾つ分にあたる数が先、基準量にあたる数が後ろに書いたものを、「基準量が後に示された問題」といいます。
用語:基準量が後に示された問題
小学校の授業や学力調査では、数の出現の順序を逆にして、かけ算の式にしたものが正解とされます。出現順に書いたかけ算の式は、「問題に出てくる数を頭の中にいったん収めて,演算の決定に導くように問題の場を組織だてる力が欠けている」「かけ算の意味を正しく理解していない」とみなされます。
向山型算数授業法事典 小学2年
- 「かけられる数」と「かける数」の区別を重視します.最初は,それらを黒板の式に吹き出しに載せ,子どもたちにも書き写させます.
- 囲みで〈ポイント〉として,「5×8と8×5との区別をする」(p.69),「あとあと,2×8と8×2との区別をするためである」(p.73)と書き,「何このいくつぶん」を徹底しています.
- pp.76-77では,「おかしのはこが4つあります。1つのはこには,おかしが5こずつはいっています。みんなでなんこになるでしょう。」という教科書からの問題を取り上げ,「かけられる数とかける数が入れ替わった文章題」を扱います.問題解決学習だとここで,「4×5=20」と「5×4=20」の式を出させて比較するところ,本文では「4×5=20」が出ることなく,板書の図を書き写させて,「5×4=20」へと導いています.
- pp.78-79(かけ算①の最後の見開き)は,作問の授業です.教科書の出題は,「下のえを見て,3×4のしきになるもんだいをつくりましょう。」です.子どもたちが問題を作ったら,先生はそれを見て,寸評とともに「4点」「1点」「10点」といった個別評定をします.「10点」でなければ作り直します.2〜5の段のかけ算へと広げて、同様に子どもが問題を作り,先生が個別評定をしていくと,そのうち「12点」という点数が出て、子どもたちはびっくりします.それは「前時にやった「かけられる数」と「かける数」が入れ替わった文章題」です.
間違いのパターンには大きく分けて2種類があります。一つは、2つの数量を単純に並べ、「かけるといくつになるでしょう」といった形の問題にすることです(「ペアはいくつできるでしょう」のように、直積に基づいたものであれば、正解となるのですが)。
もう一つは、かけられる数とかける数の意味の間違いです。その場合には
- 子どもが、かけられる数とかける数が反対の文章題を書く
- 先生は、その文章題を式と照合させる(図を描かせることも)
- 子どもが反対だと気づいて、文章題を作り直す
という展開が見られます。
用語:作問
もう一つの主張を,取り上げます.「かけ算には本来,順序がない」における「本来」を,「長方形に基づけば」と読み替えるものです.
長方形は連続的な“積”のモデルですが,離散的なものもあって,数学的には直積,算数教育においてはアレイ図です.かけ算の導入となる小学校2年でも,アレイ図が活用され,交換法則や分配法則を理解するのに役立てられています.アレイが直積に基づくこと,またそれに対する日本のかけ算指導のスタンスは,中島1968bの文献に記されています.
直積という言葉を用いないにしても,この方針もまた,算数教育において問題点が指摘されています.いままでの
「タイル×タイル」
というのは,子どもにはなかなかわからない。
「外延量×外延量」
という計算は,面積などにたしかにあるわけです。しかし,それは一般性をもっていなくて,非常に特殊な物です。それでやはり,
総量=内包量×容量
という考えに変えたわけです。
(『遠山啓エッセンス〈3〉量の理論』pp.154-155)(略)長さや重さなど,量を含んだかけ算の場面・問題に対し,かけた結果がどんな量で,答えにどんな単位を添えればいいかまで,考える必要があります.被乗数と乗数をともに「因数」として区別しない方針は,その解決を遠ざける方向に向くように思うのです.
かけ算には本来,順序がない
- 海外文献より(リンクのみ)
- 雑多なところ(リンクのみ)
「なぜかけ算に順番があるという指導をしているのか」という疑問への答えが見当たらない,というのなら,そこは,日本の算術や算数,また国外の事例をもとに,多数の実践例および学術的な根拠を見ていき,頭の中で再構成を図るなり,まとまった文章として取りまとめるのが,しんどいけれど避けられないのかなと思っています.当ブログの記載内容は,現時点でのその帰結です.
ツイート感謝
*5:繰り返しますが「数学教育学」における根拠であり「数学」ではありません.とはいえ最後の節で参考文献のみ挙げた「量の理論」も,かけ算の順序,より正確には2つの因数に当たるものの区別を前提として,構築されているのですが.