http://togetter.com/li/881076とhttp://togetter.com/li/881113も読みました.
検索エンジン経由でななめの長方形へのアクセスがありましたが,内容的には正方形・正三角形をつくるが近そうです.外を探すと,今年の3月には,小4で5㎠の正方形を作るという問題が流れました*1.
さて,最初のリンクの最初のツイートには,「面積が12cmの長方形を描こう」とあるのですが,面積なら12㎠と書くべきだし,2年で,㎠を使って面積を表すというのも不可解です.念のため,http://www.nier.go.jp/guideline/で調べたところ,昭和33年度の小学校学習指導要領以降,平方センチメートルを学ぶのは第4学年です.
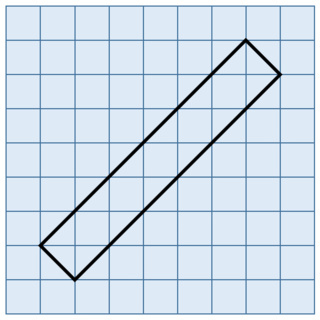
授業で出された問題は,「まわりの長さが12cmの長方形を描こう」ではなかったかと想像しました.こう置き換えると,授業のその後の展開と整合します.ななめを使った正方形・長方形の周の長さが,正方格子の最短長の整数倍となることはありません.*2
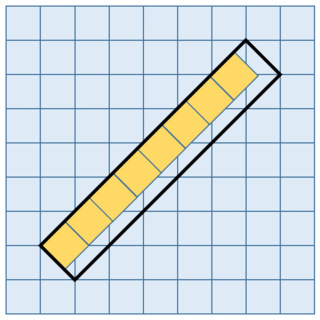
他の候補として,面積を,2年までで学ぶ用語「大きさ」に変更すると,「大きさが,(方眼紙の)1番小さな正方形の12個分になるような長方形を描こう」となります.この場合,「12個分」となるのを,小学校2年生の段階で確認するには,任意単位を用いた大きさの比較*3を使わざるを得ませんが,単位正方形を45度,回転させて,描いたななめの長方形に当てはめようにも,ちょうど12個分の大きさになるというのは困難です*4.
2年の算数の授業,また長方形や正方形の弁別という観点では,「まわりの長さが12cmの長方形を描こう」のほうが面白そうです.というのも,単位長が1cmの正方格子から4点を選んで結び,まわりの長さが12cmとなる長方形には,3種類が考えられます.各辺の長さは(1cm,5cm,1cm,5cm),(2cm,4cm,2cm,4cm),(3cm,3cm,3cm,3cm)の3種類です.このうち最後は長方形じゃなくて正方形じゃないか*5,と主張できるのです.
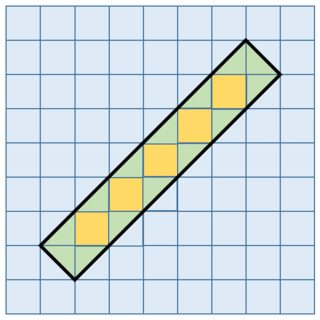
追記:図を作ってみました.順に,最初のツイートと同じななめの長方形,それに単位正方形を乗せたもの(12個分と確認できない),単位正方形と直角二等辺三角形で敷き詰めたもの(面積は,1×5+×14=12)です.
*1:http://togech.jp/2015/03/17/20727
*2:反例がありました.(0,0)と(3,4)を結ぶ線分を辺の1つとし,他の2点を正方格子上にとってできる正方形・長方形について,まわりの長さは最短長の整数倍となります.ななめを使った正方形・長方形において,1つの辺の長さが最短長の無理数倍ならば,まわりの長さも無理数倍となり,今回のななめの長方形もこの条件に当てはまります.
*3:http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2009/06/16/1234931_004_2.pdf#page=11.名称はともかく,活動・学習は1年で行われています.
*4:単位正方形を対角線で2分割して敷き詰めることを認めれば,ちょうど12個分となるのが図示できますが,算数としては面積の加法性(切ったり,くっつけたりしても,全体の大きさは変わらない)が前提となります.用語はともかく,それを1年で学習していると考えるなら,くだんの長方形は単位正方形の12個分だと,授業内で確認でき,そうでなければ---4年・5年で学習するとすれば---12個分であることが示せない,となります.