かけ算について(2016.11)

うえの子は2年生ですので，小学校ではかけ算を学習しています．
先日，机の上で，問題集を開いたままにしていたので，見てみると，「さらが 5まいあります。1さらにりんごが 3こずつのっています。りんごはぜんぶで何こあるでしょう」のタイプの文章題*1が並んでいました．
そういった出題に対し，うえの子の答案はというと，5×3＝15のように，出現する順に数を並べ，かけ算の式を書いていました．他の文章題も，同じようにしています．宿題らしく，○×はついていません．
戻ってきたうえの子に，式はそれでいいのかと尋ねたところ，あっ，と言って消しゴムで消し始めました．

「かけ算の順序」に関しては，Webでアクセスできる情報や，国内外で刊行された書籍・論文などを通じて，自分なりに記録しておき，できれば年に1個でも，知見を言葉で表せればと思っています．昨年の知見は，以下のとおりです．

(略)かけ算の交換法則を，イエスバットの構文のバットの後に使うのが，ネット上の論調なのに対し，バットの前に使うのが，国内外の算数教育の事例に多く出現します．
イエスバットの文を具体的に表すと，次のとおりです．

3×5が正解だというが，交換法則があるから5×3も正解だよ

交換法則から3×5＝5×3となるが，3×5と5×3とで表すものが異なるよ

It may be useful to focus attention on where the commutative law appears in an argument. Those who complain about the incorrectness of the red-pencil seen in imgur's picture often think that although a x b and b x a are different literally, a x b = b x a should hold by the commutative law. On the other hand, people for it seem to understand that even if they accept the commutative law of multiplication, a x b and b x a represent different things.

Order of Operationsに，エールを

なお，3×5と5×3，a×bとb×aなどの違いや，学習者の認知，そして算数教育での展開などに関しては，http://d.hatena.ne.jp/takehikom/20130204/1359989997やhttp://d.hatena.ne.jp/takehikom/20151121/1448031600で整理を試みてきました．
今年の知見として，アレイ図*2の使いどころを挙げたいと思います．具体的にはこうです：かけ算の文章題に対して，アレイに基づきその数量をイメージするのではなく，数量を認識してかけ算の式で表したあと，その積を求めるために，アレイが活用されています．

2年前に6社の算数の教科書を調査し，昨年あるスライド（あとで示します）を作っていたとき，どこかの教科書に，文章題で子どもがアレイ図をイメージしていたのがあったのが，少し気になっていました．
教科書を1冊，読んでいくと，まさにその例が載っていました．

小学算数 2下 [平成27年度採用]

出版社/メーカー: 教育出版
発売日: 2014/02/01
メディア: 単行本
この商品を含むブログ (1件) を見る

文章題はp.8にあります．ページの最初に「1本に4こずつ入ったボールが3本あります。ボールはぜんぶで何こあるでしょうか。」という問題が書かれており，テニスボール4個が円筒形ボトルに入ったカラー写真*3を添えてあります．
そのあとの小問は2つです．はじめに，「1 かけ算の式にあらわしましょう。」で，すぐ下に，式が書ける空欄もあります．教科書のこれまでの記載から，ここでは「4×3」と書くことが期待されます．次に，「2 答えのもとめ方を考えましょう。」となっており，そこでは2人の考え方が表現されています．左側のけんじさんには，「4このまとまりが3つ分だから…。」という吹き出しがついています．右側のゆみさんは，発言の代わりに，4行3列にならべた赤いおはじきをイメージしています．
その下には，「かけ算の答えのもとめ方」という小見出しで，薄い背景色のついた囲みが設けられています．「4×3の答えは，4＋4＋4でもとめることができます。」という文と，4つずつ3つ分，赤い丸があることを表した図も，そこに載っています．図のうち4個で1つ分のところは，テニスボールを図に（抽象化）したものであるとともに，ゆみさんによるアレイ図のイメージを，累加で勘定できるよう分割したものにもなっています．
このように，「文章題で子どもがアレイ図をイメージしていた」を，見つけることができました．
そうしてこれは，文章題に対するイメージ（もしくはスキーマ）ではなく，4×3という式を書いた上で，4×3＝12と計算するために示された，スキーマの1つとなっています．
アレイを含む，昨年作ったスライドを，以下に示します*4．

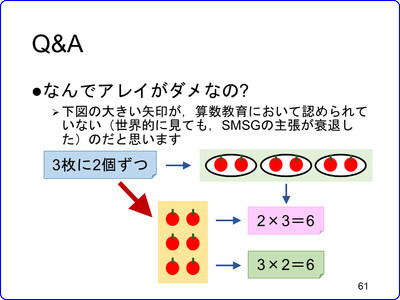
教育出版のボールの文章題の事例は，大きい矢印（のように子どもがイメージすること）を，認めるものにはなっていないのでした．
とはいえ，教科書を通じて学べることとなると，次のように，矢印を少し修正したいと思います．

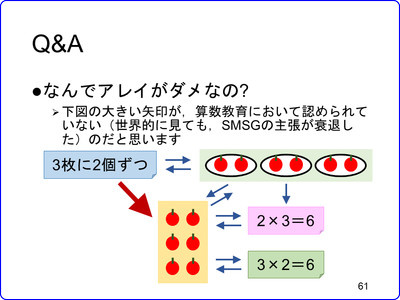
大きい矢印は依然として無効ですが，青い矢印（グラフ理論でいう有向辺）を通して，「3枚に2個ずつ」という場面が「3×2＝6」の式につながることを，示しています．
もちろん，経路が存在することと，そのように考える子どもが存在すること，授業で認められることとは別である点には，留意しないといけません．
なお，アレイに対して，かけられる数とかける数とを交換するシチュエーションは，今回の教科書ではp.31に見られます．「1れつに8人ずつ，4れつにならんでいます。ぜんぶで何人いるでしょうか。」という文章題と，式を書く欄（8×4が期待されます）のあと，「答えのもとめ方を考えましょう。」という小問で，8行4列のアレイが出てきます．けんじさんは縦方向に，またゆみさんは横方向に，赤丸を囲っています．ここから，既習の4×8＝32を使って，8×4＝4×8＝32とすることが読み取れます．この流れにおいても，8人ずつ4列の人数を4×8で表すことは，認められていません．