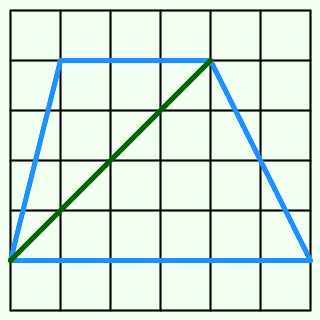
いきなりですが問題です.方眼紙(正方格子)の4点を結んでできる,以下の台形の面積の求め方を考えます.

小学校の授業で問うと,以下の4つの方法が出ました.
①
台形の左上と右下の頂点を結ぶと,三角形が2つできます.
下の三角形の面積は,6×4÷2=12です.
上の三角形の面積は,3×4÷2=6です.
合わせて,台形の面積は,12+6=18です.
②
台形の右上と左下の頂点を結ぶと,三角形が2つできます.
上の三角形の面積は,3×4÷2=6です.
下の三角形の面積は,6×4÷2=12です.
合わせて,台形の面積は,6+12=18です.
③
縦に線を入れて,長方形と,2つの三角形に分けます.
長方形の面積は,4×3=12です.
左の三角形の面積は,1×4÷2=2です.
右の三角形の面積は,2×4÷2=4です.
合わせて,台形の面積は,12+2+4=18です.
④
合同な台形を回転させ,斜めの辺と重ねると,平行四辺形ができます.
この平行四辺形の面積は,(6+3)×4=36です.
台形の面積は,その半分なので,36÷2=18です.
このうち,他の台形でも同じやり方で面積が求められないのは,どの方法でしょうか.
元ネタは,以下の本のpp.92-93です.原文では,p.92に4つの求め方を図と式*1で表しており,p.93の上部には「早く・簡単に考えることができそうなのはどれかな?」と問うています.

- 作者: 樋口万太郎
- 出版社/メーカー: 東洋館出版社
- 発売日: 2019/08/10
- メディア: 単行本
- この商品を含むブログを見る
「早く・簡単に」というので連想するのは,「は・か・せ」です.以下のページが,この本の参考・引用文献に入っていました.どちらかというと批判的な取り上げ方です.なお「はかせどん」は「速い,簡単,正確,どんなときでも」の略となっており,この「どんなときも」は,「他の台形でも同じやり方で面積が求められるかな?」という問題意識と関わってきます.
実際のところ,『算数7つの決めゼリフ』は,「は・か・せ」の批判本と見ることができます.理論編(1章)の内容がそのようになっていて,p.13の「いつでもなんでも「は・か・せ」でよいと思って使うことは,教師の「思考停止」につながっているのです。」がその最たるものです.
台形の面積の求め方を考えるという授業も,直接的な表現はないものの,アンチ「は・か・せ」です.というのも,「早く・簡単に考えることができそうなのはどれかな?」という問いに対し,p.93では「私は①のほうが早く・簡単だと思います。なぜなら~」といった子供の反応を例示する一方で,同じページの最後には,台形の公式となる「(上底+下底)×高さ÷2」を提示しており,「私は④が早く・簡単だと思います。なぜなら~」のような子供の発言*2を引き出しにくくしているように見えるからです.
といったところで解答です.①から④までの4つの求め方のうち,台形の形が変わると使えない場合があるのは,③です.具体例として,以下の台形を考えるといいでしょう.この台形の平行な辺に対し,垂直になるように線を引いて長方形を作ることが,できません.

この図形に対し,①と④の考え方は,問題ありません.次のように,2つの三角形も,2つの合同な台形を組み合わせた平行四辺形も,得ることが可能となっています.


「他の台形でも同じやり方で面積が求められないことがあるのは,③です」でおしまい,と言ってもいいのですが,もう少し考えてみると,④も正解となる余地があります.というのも,平行四辺形は,方眼紙で最初に描いた台形の範囲を超えているのです.言い方を変えると,幅6,高さ4(これらの値は与えられた台形により変わります)のサイズの方眼紙しか,使用することができないとなると,平行四辺形を描くことができないことになります.それに対し①から③まではいずれも,内部に線を入れ,台形を分割して面積を求め足し合わせるという方略になっています.
なお『算数7つの決めゼリフ』の④の図について,描き足したのは等脚台形になっており,2つの台形を組み合わせた図形は,よく見ると平行四辺形になっていません.こういう描き間違い---授業でこんな図を描いたら,子供から「それ,平行四辺形じゃないよ」というツッコミが来る---も,起こり得るのです.
「はじめに」のp.2では,SNSで,「多くの算数科に関連する愚痴が渦巻いていた」と指摘し,「さくらんぼ計算を書いていなかったら,減点された」と「分数の括線を定規を使って引かなかったから,減点された」の2項目を,「保護者の愚痴」として例示していました.この本において「かけ算の順序」は,SNSにおける愚痴の対象外らしく,それはp.48の式からもうかがい知ることができます.