いきなりですが問題です.
長方形でない平行四辺形で,ある辺を底辺とみるとその長さが4cm,高さが3cmだけれど,他の辺を底辺とみることでその長さが3cm,高さが4cmとなるような図形を図示してください.
「4cm」「3cm」をそれぞれ「a」「b」に置き換えて,判定問題にします.
a≠bとし,長方形でない平行四辺形で,ある辺を底辺とみるとその長さがa,高さがbだけれど,他の辺を底辺とみることでその長さがb,高さがaとなるような図形を作れるか?
適当に,図を描いてみると,次のようになります.左右の平行四辺形は合同(回転・平行移動すると重なります)ですが,aとbの長さは,実のところ左右で同一でありません.
最初の問題も,判定問題も,「作れない」が答えとなります.三角比を用いて説明ができます.
長方形でない平行四辺形で,底辺の長さをa,高さをbとします.この平行四辺形について長さが未知の辺の長さをxとし,隣り合う2つの辺のなす角をθとすると,と表すことができ(θ>90°の場合や,θが小さくて高さを平行四辺形の内部で示すことができないような場合でも,この式で表せます),
です.この図形は長方形ではありませんので,θ≠90°であり,
です.したがって
であり,「他の辺を底辺とみることでその長さがb」とすることができません.
続いてですが問題です.
a≠bとし,直角三角形でない三角形で,ある辺を底辺とみるとその長さがa,高さがbだけれど,他の辺を底辺とみることでその長さがb,高さがaとなるような図形を作れるか?
答えからいうと,これも「作れない」です.しかし上記と同じアプローチでは,うまく説明できないようにも思えます.三角形なので,「他の辺」が2つ,あるからです.
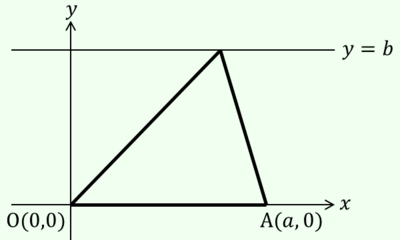
そこで,別の方法を採用します.「底辺の長さがa,高さがb」の三角形は,以下の図に基づいて作図できることから,話を始めます.
2次元座標上で,O(0,0),A(a,0),そしてBは直線y=b上の任意の点です.そのx座標をxとすると,B(x,b)です.そのようにして構成される三角形OABは必ず,「底辺の長さがa,高さがb」であり,逆に,「底辺の長さがa,高さがb」の三角形は,どのようなものであっても,回転移動と平行移動により,このような3点と合うようにできます.
2つほど,具体的な三角形を図示しておきましょう.
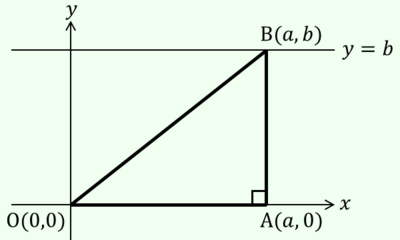
さて,この条件を満たす三角形で,長さが決まっていない辺の1つについて,それ「を底辺とみることでその長さがb」としたいのですが,線分OAが直線y=0の一部であることと,2直線y=0とy=bは平行であることから,辺の長さをbにするには,B(x,b)についてx=0またはx=bのいずれかしかありません.それぞれ,以下のようになります.
そしていずれも,直角三角形です.
a≠bで,「底辺がaで高さがb,かつ底辺がbで高さがa」となるのは,任意の平行四辺形ではなく長方形,任意の三角形ではなく直角三角形に限られる,という結論になります.
本記事は,以下の内容を少し精緻化し,三角形についても検討したものです.
平行四辺形の底辺と高さも,同じ次元(長さ)ではありますが,図形として見たとき,互いに交換するわけにいきません。底辺が5cmで高さが3cmという平行四辺形(ただし長方形ではないものとします)と,底辺が3cmで高さが5cmという平行四辺形は,どのようなペアを持ってきても,合同となりません.それに対し,縦が5cmで横が3cmの長方形と,縦が3cmで横が5cmの長方形は,常に合同です.