わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

Shampoo Boy

5×3

1. 並べ方・配り方

「5．ゼスチャー」では，たこ焼きの載ったお皿を，たこ焼きが一列になるように並べるイメージと，たこ焼きが矩形になるようにお皿を並べるイメージとの違いを問題にしている（図も描いて！）のに，たこ焼きのトランプ配りのことと誤読している。

カリフラワーは大学教育を受けたキャベツに過ぎない（＠マーク・トウェイン） | メタメタの日

たこ焼きとお皿の件は，こちらの誤読だったようです．いや，すみませんでした．どうやら，トランプ配りではなく，当雑記でかつて《積指向》と書いた分の説明を，されたかったようでした．
そうなると，関連するのは：

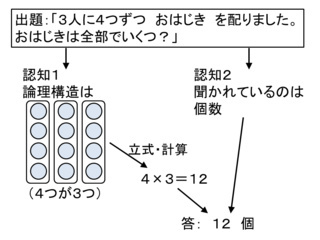
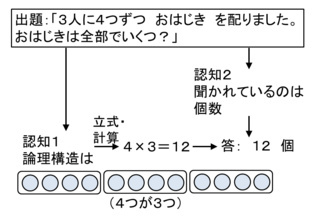
「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」（《問い》）という出題に対し(略)
これですが，《問い》は次のアレイ図に対応するというのが，算数教育に携わる者の間の共通認識になっていると思われます．

決して，次のアレイ図ではありません．

[田中2010]，[前川2011]から，知ることができます．数多くの書籍や学習指導案が，この見方に基づいています．
このように「一つ分の大きさ」と「幾つ分」を捉えることができるかを確認するよう，デザインされ，出題されています．(略)

tから学んだこと

それで，
http://ideacraft.jp/T/2011-1228-02.png
と対比するための図として

というのを描き，Twitterで報告しましたが，却下されました．その理由をもとに，

と修正してみましたが，もう連絡する予定もありませんし，採否のほどは分かりません．

なぜ教材研究

あとはリンクのみ．「配り方のCG」について，スクールプレゼンターを使うまでもなく，配り方のGIFアニメーションを作っています．最初は2010年12月だったと記憶しているのですが，最終的には，

の冒頭に置いている2つの画像でいいのではと思います．
配り方の多様性については

の中でも検討していますので，合わせてご参照いただければと思います（誰に言ってるんだ?）．

2. いくつ分×1つ分の式

いくつ分×1つ分の式を間違いとする教え方は間違っているのではないかと，学校教育を問題にしているのに，「ええ，学校教育では，間違いとなります」と，学校教育を前提にして答えている。何が俎上に上げられているのかがわかっていないようだ。（「4.式と図」）

カリフラワーは大学教育を受けたキャベツに過ぎない（＠マーク・トウェイン） | メタメタの日

「いくつ分×1つ分の式を間違いとする教え方は間違っているのではないか」について，これまで書いてきた中から，関係しそうなのを転載します．

9. 乗法の交換法則の意味するところは，そうではありません．
それでは，

  • 一つ分の大きさ×いくつ分＝全体の大きさ

によって，かけ算で全体の大きさが求められる，ということを学習して，その後，乗法の交換法則を学んだら，これらを組み合わせて，

  • いくつ分×一つ分の大きさ＝全体の大きさ

と表すこともできる，という主張でしょうか．
この主張を小学校の教育に普及させるとなると，次の課題が指摘できます．

  • 学習：乗法として利用できる方法が2種類あることになります．どちらを選ぶか，または両方書く（言う）べきか，児童はその都度考え，答えを決めないといけません．「いくつ分×一つ分の大きさ＝全体の大きさ」というルールの追加は，学習コストを高めるのではないでしょうか．
  • 構文：「３個/枚×５枚＝１５個」もしくは「３個×５＝１５個」といった，単位に基づく式のたしかめ（構文チェック）が利用できません．これは採点者だけでなく，たしかめを行う学習者にとっても損失となるのですが，代わりにどのようにして，書いた式が正しいか，チェックすればいいのでしょうか．もしくは，構文チェックのルールを追加すべきなのでしょうか（そうだとすると，上の項目と同じく，高コスト化をもたらします）．
  • 曖昧さ：５×３＝１５という式が，「５個ずつ３人に配る」という意味にも，「５人に３個ずつ配る」という意味にもなってしまいます．式と場面との対応付けが，より困難になるのではないでしょうか．
その後「×」から学んだこと

(4) 学校教育はその考え方を採用していない
「問題の場面をアレイ図で捉えること」「式に単位をつけて，“5まい×3こ/まい＝15こ”のように解釈すること」は，学習指導要領解説や，Webで知る限りの教科書，また出題例と照らし合わせて，現場教育に相容れません．
(略)
“5まい×3こ/まい＝15こ”のように，式に単位をつける方針を，学校教育に採用して欲しいという人は，数学的な土台すなわち量の理論と，その方針による小学校算数の一貫した指導方法について，構築・提案をお願いしたいと思います．
私は[銀林1975a][銀林1975b]を読み，複内包量・逆内包量といった興味深い量まで知ることができましたが，両書の中に，“5まい×3こ/まい＝15こ”あるいは“3km/(km/時)×4km/時”（[高橋2011]p.43）のような式や量の表記，そしてそれらを導出する理路を，見つけることができませんでした．

2012年に「×」から学んだこと

しかし今，読み直してみると，前者のほうは補足をしておいたほうがよさそうです．
3項目挙げた課題のうち，「学習」は，いくつ分×一つ分の大きさ＝全体の大きさとも表せることを授業において積極的に教えようとしたときの問題点です．「曖昧さ」のほうは，いくつ分×一つ分の大きさ＝全体の大きさとも表せることを，授業において積極的に教えるわけではなく，テストでそのように書いてもマルにするという場合に，日常生活への適用で発生し得る問題点と言えそうです．
それにしても，メリット・デメリットの列挙は，出尽くしたのでしょうか．あとの説明のため，比較対象になるものを，ラベリングします．

  • ある分類
    • 《P1》：かけ算の式は「一つ分の大きさ×幾つ分」で表す．
    • 《P2》：かけ算の式は「一つ分の大きさ×幾つ分」「幾つ分×一つ分の大きさ」のどちらで表してもよい．
  • 別の分類
    • 《P1》：かけ算の式は「1あたり量×いくら分」で表す．
    • 《P2》：かけ算の式は「1あたり量×いくら分」「いくら分×1あたり量」のどちらで表してもよい．

こう書いたとき，《P1》と《P2》のどちらが良いか悪いかの議論，すなわち机上の検討が，もう出尽くしたのなら*1，それぞれで授業を計画して実施してみてはどうかとなりそうです．まあそうなると，私を含め机上で議論する人々だけでは，どうしようもないのですが．
補足：「ある分類」について，もともとそこ（ただし公開前）には，「学習指導要領」と書いていたのですが，学習指導要領解説の中に「一つ分の大きさ×幾つ分」の記載はありませんでした．近いのを探ると，「（単価）×（個数）＝（代金）のような「言葉の式」」（p.58）といったところです．「別の分類」では，『かけ算には順序があるのか (岩波科学ライブラリー)』の表記をいくつか使用しています．

3. 言葉の式

思い出したことを一つ．

かけられる数＼かける数 整数 小数
整数 整数×整数（2年） 整数×小数（5年）
小数 小数×整数（4年） 小数×小数（5年）
  • 整数×整数：プリンが3個ずつ入ったパックが4パックあります．プリンは全部で幾つありますか．
  • 小数×整数：0.5gの分銅が3つで，合わせて何gですか．
  • 整数×小数：1mが100円のリボンを1.5m買います．いくらですか．
  • 小数×小数：1mの重さが1.5kgの鉄のぼうがあります．この鉄のぼう0.8mの重さは何kgでしょう．
乗法の意味の拡張

「整数×小数」の例題で，単位量あたりの金額を中途半端な整数値にすることができます．例えば「1mが55円のリボンを1.5m買います．いくらですか．」とすると，式は55×1.5＝82.5となります．実際問題としては，切り捨てて82円でしょうか．
数どうしの演算としてみると，「整数×小数＝小数（整数を含む）」だけれども，ここから「金額×割合＝金額」を得ることができたのは，ちょっと面白いです．
『算数・数学教育つれづれ草』pp.46-47からの孫引きですが，昭和35年の『小学校算数指導書』に，“（ひとつのねだん）×（買った数）＝（ぜんたいのねだん）”という言葉の式が見られます．
プログラマの観点で，こういった「言葉の式」の意義を，言うことができます．言葉の式の間で，帰納・演繹・類推が使えることです．プログラミング，その中でもオブジェクト指向の用語を使うと，帰納はスーパークラス，演繹はサブクラス*2に対応します．言葉の式をもとに式を作るのは，インスタンス化です．
これまでに書いたことと照合すると，「金額×割合＝金額」や他の関係が「整数×小数＝小数（整数を含む）」になっているのを確認するのが帰納，「整数×小数＝小数（整数を含む）」の具体例として「金額×割合＝金額」を挙げるのが演繹，「金額×割合＝金額」（もしくは「整数×小数＝小数（整数を含む）」）の式の例として「55×1.5＝82.5」と書くのがインスタンス化です．
ここまで，言葉の式どうしの関係，言葉の式と数式との関係を見ていきましたが，算数教育ではこのインスタンス化を演繹とし，いろいろな数式から言葉の式を作るのが帰納に対応するのではないか，とも思います．
帰納・演繹・類推については，《算数解説》にも書かれていますので，主要なところを引用します．

解決のための方法や結果についての見通しをもとうとするとき，問題の個々の要素や全体的な状況を観察したり，自ら試行や実験をしたりすることが役立つことが多い。また，幾つかの具体例を調べて共通性を見付けるという帰納的な考えや，類似の場面から推測するという類推的な考えを用いることもある。見通しをもつことは，問題の解決を適切にまた合理的に進めていく上で重要なものである。
問題解決の方法や結果が正しいことをきちんと示すためには，筋道を立てて考えることが求められる。それは，根拠を明らかにしながら，一歩ずつ進めていくという考えである。ある前提を基にして説明していくという演繹的な考えが代表的なものであるが，児童が算数を学習していく中では，帰納的な考えや類推的な考えもまた，根拠となる事柄を示すという点で，筋道を立てた考えの一つといえる。
算数科においては，問題を解決したり，判断したり，推論したりする過程において，見通しをもち筋道を立てて考えたり表現したりする力を高めていくことを重要なねらいとしている。こうしたねらいは他教科等においても目指しているところであるが，特に算数科の中では，帰納的に考えたり，演繹的に考えたりするなどの場面が数多く現れる。さらに算数の内容のもつ系統性や客観性から見ても，上記のねらいに最も大きな貢献ができると考えられる。
(p.23)

4. 「教師用指導書」に「かけ算の順序」はあるのか?

「かけ算の順序」という言葉に関する，当方の立場は，以下でまとめています．

  • 一方は学術文献を読んで「かけ算の順序」からの脱却を図ったのに対し，もう一方はそこに記載されている事例から「かけ算の順序」を見出した．
  • 一方は関連情報を見つけて照合を試みるのに対し，もう一方は経験をもとに結論を下している．
←「かけ算の順序」←

かつて，「順」という文字が，どのような前後関係で使われているかをリストにしたことがあります．

といったわけで，学習指導要領とその解説で，「かけ算には順序があると主張している」どころか，（かけ算に限らず）式に関して「順序」「順番」という言葉を使用していないことを確認しています．
教師用指導書での出現は，いかがでしょうか．なければ，「「教師用指導書」のすべてに，かけ算の式の順序を教えているように，と書かれているのです．」（『かけ算には順序があるのか (岩波科学ライブラリー)』p.3）は，メタメタさんの独自解釈となります．
もし教師用指導書に「かけ算の式の順序」と記載されているのなら，ネットの議論がそこに反映された可能性を意味し，画期的なことなのですが．
…それでコメントをいただきました．

　すでに，http://ameblo.jp/metameta7/entry-10461348378.html　で紹介しましたが，
小2算数の教科書（平成13年検定）の「教師用指導書」に
「数字が出てくる順に4×3＝12と書いてしまう」（東京書籍）
「示された数値の順序のちがいを見つけさせる」（啓林館）
「問題文に示されている数値の順序にしたがって立式する」（大日本図書）
などの文言が出てきます。
　こういう例を示せば納得されるのでしょうか。

http://ameblo.jp/metameta7/entry-11186945917.html#cbox

感謝です．で，リンク先を一通り読みましたが，どちらかというと，問題文中の2つの数値の“出現の順序”として，使用しているように見えます．啓林館の「児童は数値の与えられた順に立式してしまう（4×5とする）ことが多い」のところだけは，式の順序と読むこともできますが，これも問題文中の数値の出現順という意味合いが無視できません．
そんなわけで，独自解釈であるという*3，こちらの信念は維持することにします．

5. 「順序」という言葉に着目する理由

筑波大附属小学校算数研究部・企画編集『かけ算を究める』
●田中博史「かけ算の指導の系統について」27〜28ページ
　田中博史さんが，かけ算の式の順序について何と言うかは，この本で最も期待していたことだった。いつもの田中さんらしからぬ（と言えるほど，田中さんの文章を読んでいるかと言われると心もとないが）歯切れの悪さは，ネットの議論を意識し，それに反論できない知的誠実さの表れだろう。

「かけ算を究める」（筑波大附属小）について・４ | メタメタの日

田中博史氏の記事については，知的誠実さというよりは，「かけ算の（式の）順序」という言葉に戸惑いを隠せなかった，と考えています．それは「順序性」という，日常使われない言葉が，記事中に2回出現していることから，うかがい知ることができます．
では「かけ算の（式の）順序」が，黒船のように，これからの算数教育を改革していくものかというと，私はそうは思いません．「被乗数と乗数の理解」，子ども向けには「かけられる数，かける数」と書くほうが，乗法的構造（かけ算）の理解・習熟につながりやすいと考えています．
以前にも例として挙げましたが，「1本136円で，280mL入りのジュースを4本買います。代金はいくらですか。」という，条件過多の問題になると，順序は役に立ちません．「かけられる数・かける数として，どの数を選べばよいか」と考えながら，演算決定する習慣がついていれば，それまで学んだことをもとに，式を立てることができます*4．
「かけられる数・かける数」については，啓林館のサイトの中に，次の出題がありました．

3問とも《ＢＡ型》です．はてブでリンクしたPDFファイルには，《ＡＢ型》も《ＢＡ型》もあります．
もう一つ，気になることがあります．「かけ算の順序」という表記だけで，専門家からは無視されておしまいになるのでは，ということへの危惧です．数学教育のことが分かっていない，と言ってもいいでしょう．これはコミュニケーションの断絶をもたらします．
いくつか，書いてきたことをコピーします．

しかし文科省は，「かけ算の式の正しい順序を指導せよ」とは，現在は公式文書では明示していません．mixiの「算数「かけ算の順序」を考える」コミュの管理人の積分定数さんが，文科省に電話で問い合わせた際も，「文科省としては，かけ算の式には順序があるという指導をしていないし，順序はどちらでもいいという指導もしていない」という回答だったと，報告しています．
(『かけ算には順序があるのか (岩波科学ライブラリー)』, p.2)

(略)
電話をかけられた時点，そして『かけ算には順序があるのか』が十分に出回っている，現在においても，「かけ算の式の正しい順序」「かけ算の順序」「かけ算の式には順序がある」といった表現で，文科省の中の人にどれだけ理解されているのか，想像がつきません．
かけた側は，それらの言葉について十分に説明をして，了解を得たという感触があるのかもしれません．しかしその「了解」が，十分な理解の上でなのかは，やっぱり見えてきません．受けた側は，ある程度聞いたところで，現在の小学校の算数の教育・指導を踏まえていないことが分かり，あとは言質を取られないよう，「〜していないし，〜もしていない」という回答にとどめた，という可能性も，考えられます．
上の段落の「踏まえていない」は，「小学校の算数の教育・指導」に反する，というよりは，「小学校の算数の教育・指導」が過去そして現在どのようになされているかについて，理解しないまま，どうやら「俺理論」への理解を文科省に求めようとしている，とお考えください．

電話で問い合わること

24. 「かけ算の順序」が「マイナスイオン」だなんて，何を馬鹿なことを言っているのですか!

  • 「かけ算の順序」に疑問を持ち，インターネットで読める形にしたのは誰か
  • その人は，算数教育に関する実績・論文があるのか
  • 「かけ算の順序」をキーワードとする学術文献はあるのか

に注目すると，「かけ算ではかける順序はどちらでもいい」と「マイナスイオンは健康にいい」の同質性は，揺るがないと思っています．

「倍」と「積」から学んだこと

『算数・数学教育つれづれ草』pp.46-47（2011年4月19日（５円の品３個の代金の立式は「3×5」ではダメなのか））も読み直しましたが，「順序」「順番」といった語句は，見当たりませんでした．
先ほど，「コミュニケーションの断絶」と書きました．そのような断絶が生じたとき，解消するため行動すべきなのは誰なのか，というのにも注意したいものです．
着目する言葉を変えてみます．たとえば，「一つ分の大きさ」「1あたり量」「ひとつあたりの数*5」が類義語となりそうです．そして，これらのどれが使われているかによって，その文章が依拠するものが何であるかを区別できる（ように読める）という効果もあります．まあ，引用もあるかもしれないので，機械処理する際には注意が必要ですが．

6. 2010年の，かけ算の導入

新たな文献紹介です．

  • 布川和彦: かけ算の導入 : 数の多面的な見方、定義、英語との相違, 日本数学教育学会誌, No.92, Vol.11, pp.50-51 (2010).
  • Nunokawa, K.: Multiplication: introduction, 日本数学教育学会誌, No.92, Vol.11, pp.122-123 (2010).

http://ci.nii.ac.jp/naid/110007994852, http://ci.nii.ac.jp/naid/110008008954から有料ダウンロード可能です．
しかし書誌情報を確認するのに，時間がとられました．CiNiiで引くと，2件ヒットします．同一の著者・タイトル・ページなのですが，「Vol.11」と「Vol.12」があるのです．http://web.me.com/tatsuya_ds/mt/%E7%A0%94%E7%A9%B6%E6%A5%AD%E7%B8%BE.htmlの「（所収：日本数学教学会誌, 第92巻, 第11号（数学教育），第92巻, 第12号（算数教育）.）」でどうやら，同一の文章が2つの号に掲載されたと分かりました．

やっとこさ内容です．ダウンロードしたPDFファイルは，日本語2ページと英語2ページがくっついています．
式の表記については，次のように書かれています．

2年生の導入時では，被乗数と乗数を明確に区別して扱っているが，これもかけ算の意味の理解を確かにするためと考えられる．図1のみかん全部の個数を4×6＝24と表すときに，被乗数4が一つ分の大きさ，乗数6が幾つ分を表していることを大切に扱う必要がある．ただしこの意味は世界共通でなく，例えば英語ではこれを6×4＝24とするので，被乗数，乗数の意味は逆になる．なお昭和44年の「小学校指導書算数編」では，基準にする大きさのいくつ文かにあたる大きさを「表わす」ことに触れているが，表現という側面からは被乗数と乗数の意味が特に重要となる．またかけ算の学習は，例えば2の段では被乗数が2の場合に乗数を1から9まで系統的に変化させ（図2），8×2などはここで扱わないが，これもかけ算の意味を大切にしていることの一つの現れであろう．
(p.50)

Students are required to clearly distinguish between multiplicands and multipliers at this stage because this distinction helps them understand the meaning of multiplication. Teachers pay attention to whether their students understand that multiplicands express sizes of units and multipliers express numbers of groups. These meanings are reversed from the viewpoint of some educators elsewhere in the world. The amount of oranges in Figure 1 is expressed as 4×6＝24 in Japan. The expression 6×4 is not usually allowed at the introductory stage. Learning starts with multiplications in the form of 2×□ and 5×□. While the multiplier varies from 1 to 9 (Figure 2), 2×□ and □×2 are not learned at the same time.
(p.122)

「順序」「順番」は，見当たりません．もっとも近そうなのを拾い上げると，「逆」「reversed」でしょうか．
そして内容はというと，《P1》に，合致します．
したがって《P2》を推すという方々には，まず，これに勝つための理論を打ち立て，そして授業や評価を通じて（その際の批判にも応えながら），その良さを実証していってもらいたいものです．
その鍵となるのは，「子どもたちが解けるようになってほしい問題の集合」であり，それがどのように分類できるかということだと，思います．
《P1》に賛成する人々，というよりも実際の算数・数学教育では，どうなっているかというのは，個人的に整理できていて，これまで《ＡＢ型》《ＢＡ型》《Ｂ型》《複数解》，《倍の乗法》《積の乗法》といったラベリングをしてきました．
海外まで対象を広げるなら，次の2件が明快だと思います．

論文に話を戻します．この中の，「2年生の導入時では」「at this stage」も無視するわけにいきません．こうあると，ある時点からは「どちらでもよい」となります．いつになるでしょうか?
これは以前に検討しています．

ところで、「オリンピックの400メートルリレー」や「このDVDは16倍速で記録できる」、「xのk倍は」の式は、どのように表わされるであろうか。それぞれ、一般的には「4×100mリレー」、「16×」、「kx」と表される。被乗数と乗数の位置が教科書の書き方と逆になっていることに気付くであろう。この例から分かるように、乗法では、数の位置ではなく、数が意味する内容に注目して、どの数が1つ分の数であるか、いくつ分はどの数かをしっかりと読み取ることが大切である。第2学年や第3学年では、読み取った数を、「1つ分の数×いくつ分＝全体の数」と表現できることが重要であり、逆に、この立式ができているかで、数の読み取りができているかを判断できる。しかし、高学年になり、乗法では交換法則が成り立つことや外国での立式を知り、数の意味をしっかり理解できていれば、必ずしも第2学年で学んだ順序で立式することを強制しなくてもよい。
（『小学校指導法 算数 (教科指導法シリーズ)』pp.91-92）

個人的には，乗法の意味の拡張のところで，被乗数（基準にする大きさ）と乗数（割合）を意識した授業が望まれますが，その段階での出題は，《ＢＡ型》といったものよりは，「割合に当たる大きさ」を交えて，かけ算かわり算かを問うのだろうなと思っています．
平成22年度の全国学力テストのB問題の採点にあたり「乗数と被乗数を入れ替えた式なども許容する」となっていることを教えてもらった一方で，被乗数と乗数が逆だと不正解としているものについては，4年生向けに出題された事例があるのを，把握しています．

これから先はどっちでもいいです→強制しなくてもよい

7. 正しい考え方

算数・数学は，公式を公式通り暗記して，その公式に数値をあてはめることなのか？　公式を覚えていなかったり，忘れていたり，あるいは習っていなくても，問題を読んで，自分の頭で考えて，公式とは違うが正しい考え方（公式よりはまどろっこしいかもしれないが）で，あるいは公式とは言葉の順番が違っても公式と同じ考え方で解いた生徒の方が，ただ「ことばの式」を暗記して，「ずつ」が付いている数を「1つ分」にあてはめればよい，などと思っている生徒より，ずっと算数がわかっているのは確かではないのか？　そういう算数の力を育てるのではなく，「ことばの式」を「間違えずに覚える」ようにすることが，算数の授業なのか？

カリフラワーは大学教育を受けたキャベツに過ぎない（＠マーク・トウェイン） | メタメタの日

後半の“エア教育”はさておくとして，前半に，気になる言葉があります．「公式とは違うが正しい考え方」です．
その考え方が「正しい」ことを，テストのとき，どのようにして本人が確認できるのでしょうか．
そもそも，マルバツがつく対象（式，答え）が「正しい」か「間違っている」かを判定するのは誰なのでしょうか．*6
算数教育ではなく卒研指導の中で，ごく最近，そこに注意するよう指摘しました．

  • 実験手順の中に「正しい文」とありますが，何をもって「正しい」と判定しましたか?
想定質問は学生のためならず

算数・数学教育として見ても，判定するのは本人（児童，解決者）であるという観点で，書いたことがあります．

『私』すなわち遠山啓氏の基準で正誤が判定されるのではなく，採点基準に基づき採点者が判定します．
1972年の件では，2種類の採点基準が考えられます．それ以外の答えとその対応は，そのつど別途ということで．

  • ６×４＝２４はバツ，４×６＝２４はマル
  • ６×４＝２４はマル，４×６＝２４もマル

その上で…６×４＝２４はマルになるかもしれないしバツになるかもしれない，でも４×６＝２４はマルになる．だから，必ずマルになるという，４×６＝２４を書きましょう．
かつて示した，abcdeのaの求め方を言い換えると，そうなります．
そして，このような筋道を言うだけでなく，それぞれの根拠，すなわち，なぜ「６×４＝２４はマルになるかもしれない（＝マルとする解釈がある）」「６×４＝２４はバツになるかもしれない（＝バツとする解釈がある）」「４×６＝２４はバツになる余地がない」か，にも答えられる子は，かけ算はもちろん，それ以上のことを理解し表現しているわけで，今回の問題に関しては，この上ない思考の持ち主と言えます．マルかバツかを判断する，仮想的な採点者が，その子の発言のみならず頭の中に，存在しています．バツとされたあとに，トランプ配りまたは交換法則を理由として，「６×４＝２４もマルなんだよ」と言う子と比べてみて，どっちの子が将来，有望でしょうか．

マルバツを判断するのは誰?

「これでOK」「これではダメだ」を判定するのが，解決者の内にある場合も，外にある場合も，考えるべきでしょう．そして，答えが出たら終わりではなく，その見直しやふり返りを，授業でもテスト中でも，できる習慣そして時間的余裕を，持たせてあげたいものです．

8. 誤読

残念ながら，誤読している。
いくつ分×1つ分の式を間違いとする教え方は間違っているのではないかと，学校教育を問題にしているのに，「ええ，学校教育では，間違いとなります」と，学校教育を前提にして答えている。何が俎上に上げられているのかがわかっていないようだ。（「4.式と図」）

カリフラワーは大学教育を受けたキャベツに過ぎない（＠マーク・トウェイン） | メタメタの日
  • 「ここに4まいのふくろがあります。かずや君が，1まいのふくろにりんごを3こずつ入れました。りんごは，ぜんぶでなんこありますか。」に子どもが「4×3」と書いたらバツとし，正解は「3×4」だ，これがかけ算の意味なのだという指導

に反発する一方で，

  • 当雑記の2012年3月8日（九九する究めるハックする・4. 式と図）は，それがどのような背景・意図で出題され，正答率が算出されているのかを示すために書いたのに対し，「誤読」と言い，「いくつ分×1つ分の式を間違いとする教え方は間違っているのではないか」を論点にすること

は，新たなダブスタであるように見えます．

00. タイトルは?

KANのTOKYOMAN（歌詞）の一節です．
かけ算の件を調査して2年足らず，という事情もあります．
（最終更新日時：Mon Mar 12 06:19:10 2012ごろ）

*1:2つを並べ，客観的に整理した文章というのは，見たことがないし，私自身どうもしたい気分にならないのですが．

*2:いわゆるis-a関係です．ただしhas-a関係と見るほうがいい場合もあります．

*3:「教科書」「教師用指導書」をあえて参照しなくても，他の書籍・論文やWebの情報から，かけ算の指導に関する現場教育の状況は認識できる，というのも．

*4:と言いたいのですが，問題を解くとき，問題文中にあるすべての情報を使うとは限らないという知識は，持っておく必要があります．

*5:http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20101123Kakezan.htmlに頻出します．

*6:それと別に，「正しいだとか間違いだとかの対象は，答案であり，考え方ではないのでは?」という疑問もあります．関連：「記事は「（子どもに持たせたい）イメージ」を重視していると理解していますが，それでもなお，イメージは人それぞれであっても，情報として発する（式であらわすのもその一つです）際に，形を伴うことは，無視するわけにいかないでしょう．」（2012年2月28日（かけ算を究める・ファーストインプレッション））