わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

かけ算の順序問題がWikipediaに

5×3

履歴によると，今月25日に記事が作成されたとのこと．
そして，削除依頼が出ています．
存続を前提としたとき，参考文献があまりにも少ないのが，気になります．
これまで読んできた中から，関係しそうなのを，取り出してみました．


まず，学会や教師向けの解説で思い浮かぶのが：

  • 布川和彦. “かけ算の導入―数の多面的な見方、定義、英語との相違―”, 日本数学教育学会誌, No.92, Vol.11, pp.50-51 (2010). http://ci.nii.ac.jp/naid/110007994852
  • Nunokawa, K. "Multiplication: introduction", 日本数学教育学会誌, No.92, Vol.11, pp.122-123 (2010).

2年生の導入時では，被乗数と乗数を明確に区別して扱っているが，これもかけ算の意味の理解を確かにするためと考えられる．図1のみかん全部の個数を4×6＝24と表すときに，被乗数4が一つ分の大きさ，乗数6が幾つ分を表していることを大切に扱う必要がある．ただしこの意味は世界共通でなく，例えば英語ではこれを6×4＝24とするので，被乗数，乗数の意味は逆になる．なお昭和44年の「小学校指導書算数編」では，基準にする大きさのいくつ分かにあたる大きさを「表わす」ことに触れているが，表現という側面からは被乗数と乗数の意味が特に重要となる．またかけ算の学習は，例えば2の段では被乗数が2の場合に乗数を1から9まで系統的に変化させ（図2），8×2などはここで扱わないが，これもかけ算の意味を大切にしていることの一つの現れであろう．
(p.50)

Students are required to clearly distinguish between multiplicands and multipliers at this stage because this distinction helps them understand the meaning of multiplication. Teachers pay attention to whether their students understand that multiplicands express sizes of units and multipliers express numbers of groups. These meanings are reversed from the viewpoint of some educators elsewhere in the world. The amount of oranges in Figure 1 is expressed as 4×6＝24 in Japan. The expression 6×4 is not usually allowed at the introductory stage. Learning starts with multiplications in the form of 2×□ and 5×□. While the multiplier varies from 1 to 9 (Figure 2), 2×□ and □×2 are not learned at the same time.
(p.122)

乗法の場面、「1ふくろにミカンが3こずつ入っています。5ふくろでは、ミカンは何こでしょう。」は、3×5と立式される。立式は、「1つ分の数×いくつ分＝全体の数」とまとめられ、それぞれ被乗数、乗数という。ところで、「オリンピックの400メートルリレー」や「このDVDは16倍速で記録できる」、「xのk倍は」の式は、どのように表わされるであろうか。それぞれ、一般的には「4×100mリレー」、「16×」、「kx」と表される。被乗数と乗数の位置が教科書の書き方と逆になっていることに気付くであろう。この例から分かるように、乗法では、数の位置ではなく、数が意味する内容に注目して、どの数が1つ分の数であるか、いくつ分はどの数かをしっかりと読み取ることが大切である。第2学年や第3学年では、読み取った数を、「1つ分の数×いくつ分＝全体の数」と表現できることが重要であり、逆に、この立式ができているかで、数の読み取りができているかを判断できる。しかし、高学年になり、乗法では交換法則が成り立つことや外国での立式を知り、数の意味をしっかり理解できていれば、必ずしも第2学年で学んだ順序で立式することを強制しなくてもよい。
(pp.91-92)


1972年に遠山が書いたのより前の，同種の出題や論争は：

三年の乗法九々の学習で，三の段がひととおりすんで，こどもたちは三の段の九々がすらすら唱えられるようになった。そこで，教師は次のようなテストを行って，こどもがかけ算の意味を理解して，九々を適用する力が伸びたかどうかを調べてみた。

問題　３人のこどもに，えんぴつを２本ずつあげようと思います。えんぴつがなん本いるでしょう。どんな九々をつかえばわかりますか。

どんな九々をつかうかという問に対して，３×２＝６と答えたものが予想以上に多いことがわかった。これによってこどもは問題に出てくる数を，その数の意味を深く考えもしないで，出てくる順に書き並べ，その間に，かけ算記号を書き入れることがわかった。問題に出てくる数を頭の中にいったん収めて，演算の決定に導くように問題の場を組織だてる力が欠けているらしいことがわかった。そこで，その欠けていることについての再指導に入るわけである。
３は人数を表わしている数である。それを２倍した答の６は何といったらよいか尋ねてみる。それで，６人となって問題の要求に合わないことを説明する。このようにして３×２＝６とするのが誤であることを明らかにしたとする。
しかし，上のような指導だけでは，問題をすこし変えてテストしてみると，ほとんど進歩しないことがはっきりわかってきた。つまり，一方を否定するような消極的な指導だけでは，前に述べたような問題を組織だてる力を伸ばすのに，ほとんど役だたないことがわかった。これが再指導に対しての評価であって，指導の方法を修正する必要をつかんだわけである。そこで；問題解決を，同数累加の形にもどして，倍の概念をしっかり押えるように指導したのである。今度は成功した。この事実を教師が見届けたのもやはり評価である。

昭和40年（1965年）ごろ，「5円の品3個の代金の立式は，3×5ではダメなのか」の論争が大阪や神戸から湧き起こった。それは海外で教育を受けた子どもが日本に帰国して授業に臨むと，上記問題の正答は，5×3のみで，3×5はダメという指導に遭遇した。そこで，帰国した子どもの親から担任教師に対する反発が起こり，問題化していった。
(p.46)


正答率・解答率を出しているものだと：

  • 清水静海『小学校算数 これでバッチリ!計算指導』, 文溪堂 (指導のこつシリーズ), 2011年. isbn:9784894237292*3

6つのはこに、ケーキが8こずつはいっています。ケーキはぜんぶでなんこあるでしょう。
（正解）8×6
(p.72)

多い誤答
かける数とかけられる数を逆に立式してしまう。
問題文に出てきた数の順に立式してしまった子どもが、34.7%みられました。
(同)

【問５】ここに４まいのふくろがあります。かずや君が，１まいのふくろにりんごを３こずつ入れました。
りんごは，ぜんぶでなんこありますか。
① こたえを出すためのしきを書いてください。

  • 正答９名３×４（８名） // ３＋３＋３＋３（１名）
  • 誤答２５名４×３（21名） // ４＋３（２名） // ４−１（１名） // １＋３（１名）

② どうして，そのようなしきになったか，絵に書いて教えてください。

  • 式が正答で，絵にも正しく表すことができた児童（８名）
  • 式が誤答でも，絵には正しく表すことができた児童（21名）
  • 式が正答で，絵には正しく表すことができなかった児童（１名）
  • 式が誤答で，絵にも正しく表すことができなかった児童（４名）

(p.5)

問題4
7×2.4の式で求められる問題を1つ作りましょう．ただし，問2の②のような面積を求める問題はのぞきます．今まで学習したことを思い出して考えてみましょう．（式・答えは書かなくてよい．）
(p.10)

＜表4：問4の解答分類＞*6
①. 7×2.4　17.9%（57名）
②. 2.4×7　26.6%（85名）*7
③. 2.4倍　13.5%（43名）
④. その他　22.6%（72名）
＜表5：問4の正答率＞

◎正しく問題をつくれたと判断するもの（解答類型a g） 13.2%（42名）
○おおよそ正しく問題をつくれたと判断するものを含めたもの（解答類型a g b h） 21.0%（67名）

(p.5)

作問a　5×6になる算数のお話をつくりましょう
作問b　絵をみてかけ算になるお話をつくりましょう
文章題a　1はこに 4こずつ ケーキを 入れていきます 6はこでは なんこに なりますか
文章題b　おかしの はこが 3つあります 1つの はこには、おかしが 5こずつ はいっています みんなで なんこに なりますか
(p.41)

さらに、次の基準A,Bを設定した。基準Aでは、被乗数と乗数の位置を問わず正答とした。例えば、「5×6」の話を作ることが要求されている作問課題に対して「6×5」の話が作られたときも正答とした。同様に、文章題では「5×3」の式を作るべきところ「3×5」の式でも正答とした。これに対して、基準Bでは、そういった場合を正答として認めなかった。算数の正答基準として適切なのは、基準Bであると考えられる。
(p.42)

Figure 2は、小学2年生の作問課題と文章題の正答率をまとめたものである。基準AとBでの正答者数に関して、McNemar検定をおこなった結果、文章題bでのみ差がみられ(z＝3.62, p＜.01)、文章題bでは基準Bのときに基準Aのときより正答率が低い*8ことが明らかになった。その理由は、被乗数と乗数が逆になった解答が多くみられたためであった。
(pp.43-44)

Figure 3は、大学生の作問課題と文章題の正答率をまとめたものである。基準Aでは、すべての課題で正答率が100%であった。基準AとBの正答者数に関してMcNemar検定をおこなったところ、文章題bでのみ差がみられ(z＝3.32, p＜.01)、文章題bでは基準Bのときに基準Aのときより正答率が低い*9ことが明らかになった。その理由は、被乗数と乗数が逆になった解答が多くみられたためであった。
(p.44)

第2は、被乗数と乗数に対する理解の程度に関することである。小学2年生では、文章題bにおいて被乗数と乗数が逆になった解答が多くみられた。この結果から、被乗数と乗数の区別に関する理解は、交換法則を学習していない小学2年の時点で不十分である可能性が示唆される。一方、大学生についても、文章題bにおいて被乗数と乗数が逆になった解答が多くみられ、その比率は、小学2年生よりも高かった。これより、大学生は被乗数と乗数のちがいをほとんど意識していないか、または、乗法の計算式が「被乗数×乗数」で表されることを理解していないと推測される。
(p.46)


海外：

  • Multiplication sentences describe equal set situations.
    • Repeated addition and skip counting are ways to find the total (product).
  • The numbers in a multiplication sentences mean something specific:
    • Number in a group - multiplicand
    • Number of groups - multiplier
    • Total number of objects - product

（私訳：

  • かけ算の式は，それと数の等しい，決まった状況を表す．
    • 累加や，まとめて数えることは，いずれも総数（積）を求める方法である．
  • かけ算の式に現れる数には，明確な意味がある．
    • 1つのグループに含まれる数＝かけられる数
    • グループの数＝かける数
    • 対象の総数＝積）

(p.11)

  • Greer, B. "Multiplication and Division as Models of Situations", Handbook of Research on Mathematics Teaching and Learning, pp.276-295 (1992). isbn:0029223814*11

A situation in which there is a number of groups of objects having the same number in each group normally constitutes a child's earliest encounter with an application for multiplication. For example,

3 children have 4 cookies each. How many cookies do they have altogether?

Within this conceptualization, the two numbers play clearly different roles. The number of children is the multiplier that operates on the number of cookies, the multiplicand, to produce the answer. A consequence of this asymmetry is that two types of division may be distinguished.
（私訳：いくつかのグループがあって，各グループで同じ個数のモノがあるときというのが，子どもが最初にかけ算を用いる場面になる．例えば

3人の子どもが4つずつクッキーを持っている．全部合わせるとクッキーは何個か？

これをかけ算の式で表そうとするとき，2つの数は明らかに異なる役割を担っている．子どもの数は「乗数」であり，クッキーの数すなわち「被乗数」に作用して，答えとなる総数が得られる．この非対称性から言えるのは，2種類のわり算を考えることができてそれぞれ区別されるということである．）
(p.276)

For example, consider the following contrasting pair:
A rocket travels at a speed of 16 miles per second. How far does it travel in 0.85 seconds?
A rocket travels at a speed of 0.85 miles per second. How far does it travel in 16 seconds?
From a purely computational point of view both problems involve the multiplication of 16 and 0.85, but the former is more difficult to envisage as requiring multiplication for solution; many children, indeed, judge that the answer would be given by 16÷0.85 (Greer, 1988).
Results from several experiments using problems from a variety of situation classes consistently show the multiplier effect (De Corte, Verschaffel, & Van Coillie, 1998, p. 203), namely that the difficulty of recognizing multiplication as the appropriate operation for the solution of a problem depends on whether the multiplier is an integer, a decimal greater than 1, or a decimal less than 1 (Bell et al., 1984; De Corte et al., 1988; Fischbein et al., 1985; Luke, 1988; Mangan, 1986). The size of the effect, in terms of the difference in percentage of correct choices, is of the order of 10-15% for the difference between integer and decimal greater than 1 as multiplier. For the difference between integer and decimal less than 1, the size of the effect is of the order of 40%-50%. When the multiplier is less than 1, there is the added difficulty that the result is smaller than the multiplicand, which is incompatible with the repeated addition model. By contrast, the findings from these experiments show that it makes no appreciable difference what type of number appears as the multiplicand. Thus, these results for the interpretation of word problems modeled by multiplication show a clear pattern that is consistent with the theory advanced by Fischbein et al.
（私訳：例えば，次の対照的なペアを考えよう．
あるロケットは1秒間に16マイルのスピードで進む．0.85秒ではどれだけ進むか?
あるロケットは1秒間に0.85マイルのスピードで進む．16秒ではどれだけ進むか?
純粋に，計算の観点では，どちらの問題も，16と0.85をかければ答えとなる．しかし前者のほうが，答えとして乗法を使用すると考えるのが難しい．実際，多くの子どもたちが，16÷0.85を解答として選択している．
様々な分類の（乗法の）場面に基づいた出題で，実験がなされ，いずれも乗数効果，すなわち，ある問題を解く際に適切な演算として乗法を認識・選択することの困難さが，乗数が「整数」「1より大きい小数」「1より小さい小数」のうちどれであるかに依ること，を示している．効果の大きさを，正答率の差で表すことにすると，乗数が「整数」と「1より大きい小数」の間では10-15%である．乗数が「整数」と「1より小さい小数」の間では，効果の大きさは40-50%になる．乗数が「1より小さい小数」のとき，積が被乗数よりも小さくなる（累加モデルには見られない）ため，難しさがアップしている．その一方で，これらの実験の知見として，被乗数が「整数」「1より大きい小数」「1より小さい小数」のいずれであるかは，感知できるほどの違いを見せていない．乗法の文章題の解釈に関する，この結果は，Fischbeinらが提案した理論に合致し，明確なパターンを示している．）
(p.286)

ブラジルに行ったときに6の目のサイコロを見せて，「サイコロの目の数はいくつですか」と言うと，みんな「6」と言った。「どうして6と考えたの」と尋ねるとある子が出てきて，「3×2」と書いたんです。これを3×2と見たわけを聞きました。私がどうしてそんなことを聞いたかというと，式の後ろに潜んでいる感覚は，日本語圏以外では普通意味が逆です。3×2と言えば，日本では「3個のかたまりが2個ある」という意味ですが，英語圏も中国語圏もみんな「3個ありますよ，2つのものが」という意味です。
一番わかりやすい例は，陸上競技で4×100mリレーという表示がありますね。日本で正しく勉強している子なら，4mを100人で走ると言うことになる。でも，誰もそう解釈しませんね。これは世界共通で4人で走りますよ，100mずつを，という意味の表示です。日本とは式の意味が逆なんです。だから，3×2とブラジルの子が書いたから，あえてちゃんと聞いてみたいと思ったんですね。そうしたら，はじめに出てきて説明した子は3個ずつのかたまりを作ってそれが2つ分と言いました。おやっ，これは日本と同じだぞと思っていると，他の仲間みんなが違う違うと言うのです。要するに間違っていたのです。どこの国も同じですね，間違える子がいるのは。本当は2個のかたまりが3個分だと別の子が説明してくれました。
(p.138)

It does not matter which order numbers appear in a multiplication sum because the answer will be the same either way. Two methods of the same multiplication are shown here.
（和訳本による対訳：
かけ算を式に書くときの数の順序はあまり重要ではありません。答えは同じです。
同じかけ算の二通りの考え方を示してみましょう。）
(p.19)

Q: で，wikipedia:かけ算の順序問題の内容には賛成ですか?
A: 設置そのものに異論はありませんが，数学だけでなく，算数・数学教育の観点・事例を踏まえた情報の充実をお願いしたいですね．
Q: 文献の羅列ですか?
A: 文献紹介は自分の活動のいくらかを占めていますが，すべてではありません．これまで，読んだり考えたりしたことを取りまとめてきた（アレイ図, かけ算指導案, サンドイッチ，小話集）ほか，英訳（1, 2）を試みています．書きながら作ったプログラムなどの一覧も整備しました．
Q: 学校教育は，一体どうなっているんでしょうか?
A: 去年あたりから，教科書そして教師・家庭向けの書籍で，“一方が「a×b」，もう一方が「b×a」で表されるような一対の場面（文章題，絵など）”をよく目にしています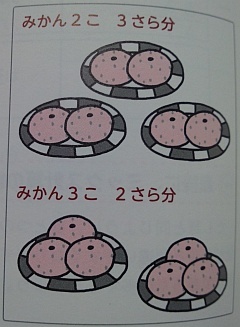（, ）．これは，「どっちでもいい」対策になっています．さらに，区別があやふやになったという子どもに，そのペアを見直させれば，「一つ分の大きさ（かけられる数）」と「幾つ分（かける数）」の区別を思い出しやすいことから，リファレンスの役割を果たすようにも思います．
Q: 学習指導要領には，かけ算の順序について書かれていないと聞いたのですが，本当ですか?
A: かけ算を含む計算に対しては，「〜の順序（順番）」という言葉を使っていません*13．とはいえ，最新（平成20年告示，算数は平成21年度から先行実施）の学習指導要領では，「小数×整数」は4年，「小数（整数を含む）×小数」は5年，「分数×整数」は5年，「分数（整数を含む）×分数」は6年となっていまして，かけられる数とかける数の区別は，高学年でもなされています．
Q: 高学年になっても，かけ算には順序がある，ということですか?
A: 正誤判定という面では，高学年では重視されません．平成22年度以降，全国学力テストの解説資料には「乗数と被乗数を入れ替えた式なども許容する。」という注意書きが入っています．なぜ高学年でそうなっているのかというと，演算決定の出題は主に“かけ算か，わり算か”を問うようになること，面積などの〈乗数と被乗数を区別しない文脈〉が現れること，比例の表で横方向に見る関係のかけ算（倍概念）のほか，縦方向に見る関係のかけ算（かけることで単位が変わる）が考えられること，あたりが思い浮かびます．
Q: 小学校のかけ算と，数学との架け橋になるものは，ないのでしょうか?
A: 小学校の話だと，Vergnaud, G. "Multiplicative Structures", Acquisition of mathematics concepts and processes, Academic Press, pp.127-174 (1983).でしょうか．一つ上の回答の「かけることで単位が変わる」も，そこに書かれています．高校の物理化学との関連では，「複比例」が大事だと思います．理想気体の状態方程式PV＝nRTが得られるのも，複比例のおかげです．
Q: 「式」って，何なんでしょうか?
A: 算数・数学における式とは何だろうか，という疑問と理解しました．『数学教育学研究ハンドブック』のpp.83-94が「文字式」というセクションになっていて，小学校の「式に表す」や「式をよむ」も含まれています．「かけ算の順序」は陽に現れませんが，こういうのを読むことで，かけ算の指導の周辺にあるものを把握していくというのは，いかがでしょうか．
Q: 他に知っておくべきURLはありますか?
A: インターネット上で，「掛け算の順序」と表記されている最も古いものかなあ．知っている最古はhttp://www.math.tohoku.ac.jp/~kuroki/keijiban/a0018.html#a19980821195612です．

Q: このエントリの出典や内容を，Wikipediaに載せよということでしょうか?
A: 全部載せたら，バランスが変におかしくなるでしょうね．せいぜい，記事を編集できる人の目に留まり，記事内容がゆっくりとでも変わっていくのを望むとします．
Q: Wikipediaのアカウントを取って編集しないの?
A: 今さらでしょう．ブログにはブログでと書きましたので，WikipediaにはWikipediaで，と思うことにします．
Q: 教科書や，先生の指導には順序があっても仕方ないけれど，○×をつけるときに，押しつけるのはよくないのでは?
A: 「○×をつける」を言うとき，教育評価の話が欠かせません．『教育評価 (岩波テキストブックス)』を読んでみるのはいかがでしょうか．学力テストや「目標に準拠した評価」など，現代の教育評価で知っておくべきことが記されているほか，「かけ算の順序」のことも書かれています．*14
Q: 図にすれば，交換法則は明らかじゃないの?
A: 学習指導要領解説の記載では，アレイ図は交換法則を得るためではなく，「一つの数をほかの数の積としてみること」の説明で使われています．同解説を越え，授業や問題集でも，用意された場面や図から，「一つ分の大きさ」と「幾つ分」の（複数の）ペアを子どもたちが発見し，それぞれ式で表す事例を知ることができます．遠山が取り上げた件ほか，論争で見かけるかけ算の文章題は，その書き方から「一つ分の大きさ」にあたる数が一つに限定されます（そのように教師・児童は認識します）．りんごのかけ算もご覧ください．

Q: かけ算の順序問題の本質って，何だと思いますか?
A: 算数教育（あるいは数学教育学）の蓄積を恣意的に取り上げて批判する人々の存在，でしょうか．
Q: 「6×4，4×6論争にひそむ意味」を書いた遠山啓も，算数教育の素人ってこと?
A: いいえ，著書を目にする限り，算数・数学教育の理論にも実践にも深く関わった人です．かの記事が出されたのち，様々な授業（実施・観察）や教材作成を通じて，乗法の意味の指導についてノウハウが蓄積され，氏の主張のいくらか（例えば，トランプ配りの乗法への適用）が「過去のもの」になっただけだと，理解しています．

（リリース：Mon Oct 29 19:55:08 2012ごろ）

（最終更新日時：Sun Nov 11 18:42:21 2012ごろ）

*1:小学校学習指導要領　算数科編（試案）（昭和26年12月5日発行，文部省）

*2:引用は，佐藤俊太郎“5円の品3個の代金の立式は「3×5」ではダメなのか”(pp.46-47)の先頭部分です．当該記事では昭和53年の『小学校指導書 算数編』以降，現在まで，5×3，3×5の両方を正答としています．

*3:問題文と正解率は，http://www.sokyoken.or.jp/kanjikeisan/keisan_h18.xhtml末尾のPDFファイルでも確認できます．

*4:3年のかけ算を指導する前に実施したレディネステストである点，式が先，考え方が後の順で出題している（考え方が先，式が後の順に出題していたら，式の正答者数が増えていた可能性がある）点には，注意が必要です．

*5:5年でも「かけ算の順序」を正誤判定に入れている調査事例です．

*6:原文には解答類型a-d，e-f，g-i，j-mで4つの表がありますが，引用しませんでした．

*7:引用者注：この行と解答類型eおよびfについて，原文は「7×2.4」となっています．前後を読めば「2.4×7」の誤記と判断できるので，引用にあたり書き換えました．

*8:正答者数や正答率の数値が本文にありませんが，Figure 2を読み取ったところ，文章題bにおける基準Aの正答率は100%にほんのわずか足りず，基準Bの正答率は80%を少し超えたくらいです．

*9:正答者数や正答率の数値が本文にありませんが，Figure 3を読み取ったところ，文章題bにおける基準Bの正答率は30%台です．

*10:英訳された日本の教科書（東京書籍，平成元年学習指導要領準拠）を参照しながら，かけ算の指導法や式の表し方を紹介しています．このPDFファイルは，wikipedia:en:MultiplicationのNotesの1番目でリンクされています．

*11:被乗数と乗数の区別を明確にしています．なお，それらを「×」の左右どちらに書くべきかについては，特に示されていません．

*12:個人的には，引用の最後の文にある説明は，「3×2と書いたら，2個のかたまりが3個分になるんだよ」だと解釈しています．

*13:学習指導要領解説を見直したところ，「第4学年では，(略)計算の順序についてのきまりなどを理解し」という記述がありました．これはすぐ次のページで，括弧優先と乗除先行という形で具体化されており，「かけ算の順序問題」とは別物です．

*14:とはいえ過去のエントリを：教育評価，2冊目, 教育評価