
教科調査官が語るこれからの授業 小学校―言語活動を生かし「思考力・判断力・表現力」を育む授業とは
- 作者: 水戸部修治,笠井健一,村山哲哉,杉田洋,直山木綿子,澤井陽介
- 出版社/メーカー: 図書文化社
- 発売日: 2012/08/01
- メディア: 単行本
- この商品を含むブログを見る
とはいえ,関心はやっぱり算数です.教科調査官の説明から,抜き出します.
(略)そこで「12個のキャンディーがあります。これを3人で等しく分けましょう,というときに,どんな図を描きますか」と。2時間目は数を変えました。
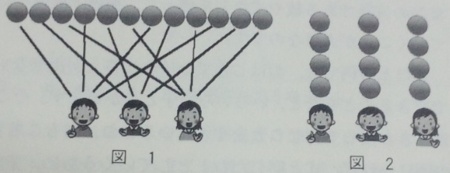
このとき1個ずつ線を引いて分けていく子どももいれば(図1),子ども3人の図を描いておいて,そこに1個ずつ置いていくやり方もあります(図2)。これらはどこのクラスでも描く子どもがいると思います。「全部で12個だ。1人が4つずつになった。3人で分けた」ということを表すのに,この2つの図ではどちらがわかりやすいでしょうか。
わかりやすいのは図1よりも図2です。図2だったら,1人分が4つずつということも,3人で分けたということも,4×3=12で全部で12個あるということも見てわかります。「こういう図を書くとわかりやすいね」ということになると思います。そして,「1人分が4個ということも3人で分けるということもわかる図だね」ということを2時間目に押さえるのです。しかも,この図だったら,4×3=12という式に直すことができます。3時間目につなげることが出きます。このように,1時間目は具体物を「分ける」という操作をして答えを求めることが目的でしたが,2時間目は図を使って答えを導くことが目的になるのです。
(p.71)
トランプ配りの等分除への適用です.最近貼り付けた,dealing outも,直線に並べておいてそれを配っているのでした.
遠山啓は,トランプ配りが乗法の立式に適用できると主張しました.したがって上の話であれば,3×4=12も,その場面をあらわしたものとなります.それを理解するには,図1の丸の並びを,3つずつ囲っていくか,図2で,段ごとに囲むのでもいいでしょう.
上の記述は,図1も図2も,これをかけ算の式で表すなら,4×3=12のみであることを示唆しています.トランプ配りの乗法への適用が「過去のもの」であるという,一例が,追加されたように感じました.
ところで,1時間目・2時間目・3時間目という表現が出ています.これはどうやら,授業に3時間かけて,等分除*1を学習するようです.それぞれの時間の違いが,p.72で図となっていました*2.

「□×3=12」を見て,包含除と等分除 再考に書いた,九九の話を思い出しました.