当記事は古い内容となっています．わり算，包含除・等分除，トランプ配り (2016.05)が最新です．
かけ算とわり算，わり算の意味としての「包含除」と「等分除」，そして「トランプ配り」について，文献と，過去に書いたことを見直しながら，知識の再構築を試みました．
かけ算とわり算，包含除と等分除―図にすると
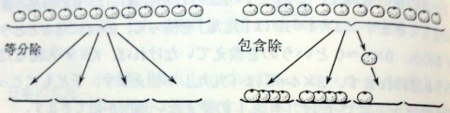
2種類のアレイ図から共通点を探ると…オレンジの囲みがいくつできるか，というのが包含除で，一つのオレンジの囲みの中に，青い丸がいくつあるか，というのが等分除です．
かけ算とわり算，包含除と等分除―言葉だと
かけ算の式の言葉による表現として，「一つ分の大きさ×いくつ分＝全体の大きさ」を採用します*1．
この関係式のもとで，「全体の大きさ」と「一つ分の大きさ」が既知のとき，「いくつ分」を求めるには，「全体の大きさ÷一つ分の大きさ＝いくつ分」とします．この形のわり算を，包含除といいます．
「全体の大きさ」と「いくつ分」が既知のとき，「一つ分の大きさ」を求めるには，「全体の大きさ÷いくつ分＝一つ分の大きさ」とします．この形のわり算を，等分除といいます．
「3個ずつミカンを持った子どもが5人います。ミカンは全部で何個ですか」がかけ算の問題（式は3×5＝15）なのに対し，「15個のミカンを3個ずつ配ります。何人の子どもに配れますか」が包含除（15÷3＝5），「15個のミカンを5人に同じ数ずつ配ります。1人は何個になりますか」が等分除（15÷5＝3）となります．
包含除・等分除という言葉は，学習指導要領の解説（『小学校学習指導要領解説 算数編』の第3学年と第5学年）に書かれていますが，授業の中で用いたり，子どもたちがその名称を覚えたりするということは，ありません．数学教育協議会（数教協）などの取り組みの中で，「ドキドキわり算」「ニコニコわり算」と呼ばれることがあります．等分除を，「トランプくばり」の操作に結びつけて学習するのは，数教協に限りません．
学年が上がり，割合を指導するときにも，一つのかけ算に2種類のわり算が登場します．B×p＝Aで表される関係があるとき(B:base, p:proportion, A:amount)，割合pを求める式p＝A÷Bを，比*2の第一用法，Aを求める式A＝B×pを，比の第二用法，Bを求める式B＝A÷pを，比の第三用法と呼びます．3つを合わせて比の3用法といいます．第一用法は包含除，第三用法は等分除の拡張です．
数教協に関わってきた遠山啓や銀林浩の著書によると，「度の3用法」と「率の3用法」に分かれます．指導にあたっては，率よりも度を重視しています．率の3用法は，上とほぼ同じです．度の3用法では，1あたり量（または内包量）*3を求める等分除のほうが，第一用法となります．
戦前は
包含除・等分除という言葉は，昭和初期の書籍からも見ることができます．木村教雄『小学算術教材ノ基礎的研究』（培風館，1936）のp.23には
とあり，脚注に「包含除の本質は累減にあると見ることが出来る．」と書かれています．
この前後では，a×b＝cからaまたはbを求めるのを割算と称し，いくつかの用語を定義しています．そして「次の二つの場合」とし，(1)が上記の包含除で，例文を文字にすると，「12銭は4銭の幾倍か（幾つ含むか）」です．ページをめくって，(2)が等分除です．等分除の例文は，「12銭は幾銭を4倍したものか．（四つに等分するとその一つ分は幾らか）」です．そのあと，乗法の交換法則を理由に挙げ，「積と一因数を知って他の一因数を求めるものである」と，まとめています．
昭和50年代は
『整数の計算 (リーディングス 新しい算数研究)』は，新算数教育研究会の機関誌「新しい算数研究」から論説を精選し，テーマごとに章分けするとともに解説を入れています．第4章が「除法の意味」となっており，1978〜1980年（昭和50年代前半．ただし1件だけ，1985年のものがあります）の論説や研究事例を読むことができます．
章のはじめの解説(pp.130-131)では，包含除（から指導を始めること）が優勢のように見えます．
“配り方”についてもp.145（長田耕一「わり算の意味と方法についての具体的展開」）で挙げられています．「包含除の場合は，同数累減という操作で処理できる」「被乗数先唱で九九を唱えれば，除数を先唱して商を見つけることになる」といった理由を挙げ，包含除から導入することの分かりやすさを指摘しています．
ここでなぜ，包含除のほうが分かりやすいのか，そして「被乗数先唱」が出てくるのかを，上に書いたミカンの問題をもとに，確認しておきます．「15個のミカンを5個ずつ配ります。何人の子どもに配れますか」（包含除）に対して，わり算を知らない（または除法を乗法と関連づける活動として）状況で表したかけ算の式，5×□＝15から，□を求めるのは九九の五の段が使えます．すなわち「五一が5，五二10，五三15」として，□は3となります．一方，「15個のミカンを5人に同じ数ずつ配ります。1人は何個になりますか」（等分除）に対する式，□×5＝15から，□を求めるのは，何の段を使えばいいか分からない分，手間がかかるというわけです．なお，5×3＝20を「五三15」というのが被乗数先唱，それに対し3×5＝15を「五三15」というのが乗数先唱です．
とはいえ，『整数の計算』には，等分除を先，包含除を後とする指導法も入っていまして，pp.156-159（正木孝昌「整数の乗除の意味と計算指導のキーポイント」）にあります．その根拠として「等分するという生活経験が子どもには多いし，問題場面の理解が容易」を挙げています．被乗数先唱・乗数先唱の件は，「かけ算の交換則を認め，自在に使っている子どもだから」により，うまくいくとしています．
優劣ではないのですが，黒表紙時代の考え方が書かれているものが興味深かったので，抜き書きします（同ページには，緑表紙ではどう対応しているかについても，記されています）．
しかも，除法における演算決定の困難性を次のように，加減乗と異なる二義性にあると説く．
整数四則算法のうち，最も児童の了解に困難を訴ふるのは除法である．(略)即ち，等分・包含といふ派生的の二義的観念が算法の本質をなして居る．この二義性が児童を昏迷せしむる所以である．*4
かくして「算法は四則にあらずして五則なり」などという見解も流布された．また「なぜ割るのか」の判断基準を包含・等分の意味に求めることの重要性が指摘され，等分を「つ割」，包含を「ずつ割」などと称して，意味の徹底を図ろうとする試みさえ出現するにいたった．(略)
(p.137．杉山政衛「整数のわり算―その意味と方法―」)
外国の教科書に基づく論説も，収録されています．杉山吉茂「アメリカにおける除法の意味と計算」(pp.139-142)で，先頭から2番目の段落に，「包含除，あるいは同数累減といった立場で指導を展開している教科書が多い」とのこと．それと対比する形で，最初の段落は日本の（昭和50年代前半あたりの）算数指導が述べられており，「ほとんど同時にとりあげる」となっています．
現在は
算数・数学教育に関する理論的・実践的研究の集大成として2010年末に出版された『数学教育学研究ハンドブック』では，第3章§2（演算の意味・手続き）の中で，除法の意味づけについて記されています．「除法は，乗法を割合で意味づけた場合，基準量を求める場合と割合を求める場合の2つがある。それを別々にせず，乗法の逆演算ということで意味づけることもある」(p.74)とあり，これのみを見れば両論併記ですが，以降では，別々にしない意味づけでの指導方法が見られず，直後の段落には「等分除」と「包含除」が，そして次ページの結論に関わる中に「整数÷整数の包含除」が書かれています，そういったことから，主流となる考え方・教え方は「包含除と等分除をともに学習させること」「包含除を主とすべきこと」なのが読み取れます．
包含除と等分除の区別を知っておくのには，いくつか意義があります．一つは，子どもたちが問題に取り組むときに，「あ，これはわり算だ!」と判断できるようになることです．大人の立場でも，数や量の構成（ものの見方）をより豊かにすることができます．
加えて，現在の日本の教育では「言語活動」，算数においては「算数的活動」のウエイトが高まっています．そうしたとき，ある出題（文章題，場面）に対して，子どもたちが答え（個数，人数など）だけ，あるいは式と答えだけを書くのでは不十分であり，その判断・根拠を説明できるようになることまでが期待されています．包含除と等分除の区別は，演算決定の根拠をより明確にし，算数（数学）と日本語を結びつけたコミュニケーションを図りやすくするのに寄与すると言えそうです．
最近の指導例
『算数科「問題解決の授業」に生きる「問題」集』では，次のような，わり算の問題と授業例が紹介されています(p.85)．
文字にしておきます．
第3学年 D 数量関係
わり算 わり算が用いられる場面
問題43
12このクッキーを絵のように分けました。
式にあらわすと，どちらが正しいでしょうか。
ア 12÷4
イ 12÷3
どちらが正しいか予想させると，「アが正しい」，「イが正しい」，「どちらも正しい」に分かれます．それぞれの考えを説明し合う中で，クッキーの置く手順の違いや，「○人に分ける」や「○個ずつ分ける」など，分け方の違いを確認していきます．そして教科書を用いて「わり算は，同じ絵でも式が違う場合がある」ことをまとめる，としています．
というわけで，問題文は「どちらが正しいでしょうか」ですが，結論は「どちらも正解」という授業でした．
その次のページでは，「リボンの長さを5倍すると30mになります。リボンの長さは□mです。」の式に「ア 30×5＝□」「イ 5×□＝30」「ウ □×5＝30」を提示しています．そしてアとイはおかしく，ウが正しい，と展開します．これも第3学年でして，「□を使ったかけ算」の問題と授業例です．
海外では
Vergnaud (1983)では，Vergnaudと銀林氏の「かけ算の意味」で引いたとおり，"first-type division"，"second-type division"という名称を挙げています．
Greer (1992)については，Greerによる，乗法・除法が用いられる場合で紹介しましたが，〈乗数と被乗数が区別される文脈〉だと一つのかけ算に2種類のわり算，〈乗数と被乗数を区別しない文脈〉だと一つのかけ算に1種類のわり算，として乗除の関係が表になっています．
英語で読める，新しい指導の体系として，米国のCommon Core State Standards for Mathematics (Core Standards)があります．3年向けの学習内容としてp.23に，次のように書かれています．
1. Interpret products of whole numbers, e.g., interpret 5 × 7 as the total number of objects in 5 groups of 7 objects each. For example, describe a context in which a total number of objects can be expressed as 5 × 7.」と「2. Interpret whole-number quotients of whole numbers, e.g., interpret 56 ÷ 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each. For example, describe a context in which a number of shares or a number of groups can be expressed as 56 ÷ 8.
そこでもまた，かけ算は1種類なのに対してわり算は2種類であること，そして等分除と包含除を区別して（いずれもわり算で求められる事例として）扱うことを示唆しています．
Core Standardsのp.89では，かけ算とわり算の問題や式が，以下のとおり表になっています．
表の中段，「Area example」を見ると，18 ÷ 3 = ?によって求める問題は
Area example. A rectangle has area 18 square centimeters. If one side is 3 cm long, how long is a side next to it?
で，18 ÷ 6 = ?によって求める問題は
Area example. A rectangle has area 18 square centimeters. If one side is 6 cm long, how long is a side next to it?
となっており，違いは「3cm」と「6cm」だけです（それ以外の場面では，2種類のわり算の文がそれぞれ異なっていることも，確認できます）．これもまた，特別な種類のかけ算に対しては，わり算の式が実質的に一つであることを補強しています．
歴史的にも国際的にも，初等教育における除法には，2種類の意味づけがあると言っていいでしょう．
他の種類のかけ算・わり算
上に書いた「特別な種類のかけ算」や「〈乗数と被乗数を区別しない文脈〉」について，少し書いておきます．
「一つ分の大きさ×いくつ分＝全体の大きさ」（それと同様の式を含みます）に基づかないかけ算もあるというわけです．そしてそこでは，わり算の意味づけが異なってきます．
例えば，「縦の長さ×横の長さ＝長方形の面積」を用いた場合，「長方形の面積÷縦の長さ＝横の長さ」と「長方形の面積÷横の長さ＝縦の長さ」という式を得ることはできますが，これらは実質的に同じ式となります．〈乗数と被乗数を区別しない文脈〉では，一つのかけ算の式に対応するわり算の式は（実質的に）一つです．
面積のわり算は，2008年発行の小学校学習指導要領解説 算数編にも見ることができます(p.159)．「そして，（縦）と（横）から（面積）が求められるという見方に加えて，（面積）と（横）から（縦）を求めることもできるというような，公式の見方ができるようにすることも大切である。」と記されています．
「（面積）と（縦）から（横）を求める必要はないのか?」といった疑問に対しては，「『面積＝縦×横』は，『一つ分の大きさ×いくつ分＝全体の大きさ』とは異なる種類のかけ算なんだよ」というのが，回答となります．
『数の科学―水道方式の基礎 (1975年) (教育文庫〈7〉)』第4章§4では，除法の意味として「A. 1あたり量の第1用法」「B. 1あたり量の第3用法」「C. 直積型の逆算」「D. 包含除」「E. 等分除」という5種類を挙げています*5．DとEは，「倍」の逆算です．Cについては，「xy＝zにおいて，2つの量xとyはまったく対等だから，その逆演算は1つしかない」(p.116)としています．
トランプ配り
「一つ分の大きさ×いくつ分＝全体の大きさ」に立ち返ります．この式（乗法）と，包含除・等分除に対して，トランプ配りを用いて視覚化・手順化を試みている事例が豊富にあります．そこで以下のとおり，名称をつけておきます．
- トランプ配りの乗法への適用：トランプを配る操作により，「一つ分の大きさ×いくつ分＝全体の大きさ」を視覚化・手順化すること
- トランプ配りの包含除への適用：トランプを配る操作により，「全体の大きさ÷一つ分の大きさ＝いくつ分」を視覚化・手順化すること
- トランプ配りの等分除への適用：トランプを配る操作により，「全体の大きさ÷いくつ分＝一つ分の大きさ」を視覚化・手順化すること
文脈から明らかなときは「トランプ配りの」を取り除きます．この3種類の中で，事例として最も多いのは，等分除への適用です．しかし乗法への適用，包含除への適用についても，見るべき記述があります．
トランプ配りの乗法への適用をはじめて示したのは，遠山啓です．「6×4，4×6論争にひそむ意味」と題する記事が1972年の科学朝日に掲載され，『遠山啓著作集数学教育論シリーズ 5 量とはなにか 1 (1978年)』pp.114-120から読むことができます．同年1月，朝日新聞に掲載された論争（テスト問題は「6人のこどもに，1人4こずつみかんをあたえたい．みかんはいくつあればよいでしょうか」）に対し，
ミカンを配るのに，トランプを配るときのやり方で配ると，1回分が6こ，これを4回くばるのだから，それを思い浮かべる子どもは，むしろ，
6×4＝24
という方式をたてるほうが合理的だといえる。
(p.116)
と記しています．遠山と親交のあった数学者による著書，具体的には森毅『数の現象学 (ちくま学芸文庫)』（pp.67-68; 次元を異にする3種の乗法）および矢野健太郎『おかしなおかしな数学者たち (新潮文庫)』（pp.121-124; 遠山啓 - カード式配り型）にも，同様の手法が書かれています．
トランプ配りの包含除への適用は，1961年の『算数に強くなる水道方式入門 (1961年)』から見ることができます．そこでは，〔包含除の指導系統〕の中に，「a トランプ配り型」「b キャラメルの箱入れ型」が入っています(p.244)．「トランプ配り」の右には，「※ 1あたりいくつということ，減っていく過程，おわりにいくつに分けられたかハッキリわかるような問題」というコメントがついています．
とはいうものの，同書の〔等分除の指導系統〕(p.233)と合わせて，見ておく必要があります．それは，次のようになっています．
〔等分除の指導系統〕
1 分離量÷分離量
a トランプ配り型 ※等分するということ，1当りいくつということがだれでもハッキリわかるような問題
(a) 余りなし (b) 余りあり
b キャラメルの箱入れ型 ※キャラメルを箱に入れると，1当りの量が見えなくなる。連続量の除法へのつなぎとなる。
(a) 余りなし (b) 余りあり
2 連続量÷分離量
余りなし
3 連続量÷連続量
余りなし
(pp.243-244)
当時は，「トランプ配り」は具体物を使った等分除の導入であるとと同時に，「キャラメルの箱入れ」という操作と対比される手法であったのが読み取れます．そして，それらの対比は包含除でもつくることができる，ということです．
なお，1971年の『新版水道方式入門』では，トランプ配りは等分除への適用のみとなっています．
それでは，最も多い，トランプ配りの等分除の事例を見ていきましょう．
■算数に強くなる水道方式入門 (1961年)
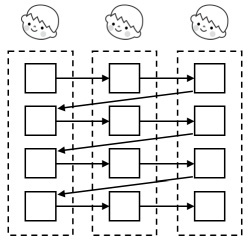(p.242，再現)
■Anghileri＆Johnson (1988)
(FIGURE 6-1, p.147)
[f:id:takehikom:20130227051639j:image](p.156)
[f:id:takehikom:20130227051640j:image](p.160)
■Greer (1992)
（p.281; dealing out）
■教科調査官が語るこれからの授業 小学校―言語活動を生かし「思考力・判断力・表現力」を育む授業とは
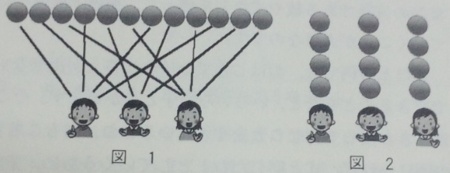（p.71; 2012年のトランプ配り）
■アイディアシートでうまくいく! 算数科問題解決授業スタンダード
（pp.57-58; 関連：2. どっちの式でもいいのかな - 北数教）
4.1.2 除法の素地
先に述べた乗法の素地となるような経験は，見方を変えれば，いずれも除法の素地にもなっている。例えば，数えることに関しては，「8個のみかんは，2個ずつまとめて数えると4回になる。」などという見方ができるようにする（図1）。これはまた，減法で表すと，8−2−2−2−2で数え終えたことになる。
また，分配を，計算とは別に，実際にそうさせることもある。例えば，「8個のみかんを4人に分けるにはどうしたらよいだろう。」などという場面を考え，各人に1個ずつ配り，まだ余りがあったらまた1個ずつ配るという活動をさせる。
(pp.144-145)
（図1，再現）
■算数科「問題解決の授業」に生きる「問題」集
（p.85; 3年のわり算かけ算）
■数学の学び方・教え方 (岩波新書 青版 822)
(p.88)
(p.89)
トランプ配りの等分除への適用は，数が多いだけでなく，英語の文献でも見ることができます．また，分ける対象を一列に並べているものと，アレイ図で表現するものが見られます．
『数学の学び方・教え方』もそうですが，遠山の著作では（例えば『遠山啓エッセンス〈3〉量の理論』），トランプ配りによって，分離量においては等分除・包含除の意味の転換が可能であることが述べられています．どうやらこれは遠山独自の考えであり，トランプ配りは等分除を累減の操作により可視化・手順化したものであることが，算数教育において確立されていると言っていいでしょう．
ところで，『数学の学び方・教え方』では，3匹のウサギの耳はいくつか求める際，かけ算の式は2×3ですが，計算する際のたし算は，2＋2＋2，3＋3ともに正しいこと(pp.34-35)，そしてタイルを用いて2×3の意味づけを図ること(pp.84-85)が述べられています．しかし1979年の講演で，ウサギの耳は2×3のシェーマとしてはあまりうまくないこと，そして「タイル×タイル」というのは子どもにはなかなかわからないことを話しています．どのようなシェーマが良いのかを含め，こちらで該当部を抜き出していますので，関心のある方はご覧ください．
Wikipedia
wikipedia:除法では，「初等教育における除法」として，次のように書かれています．
除法には、等分除と包含除という2種類の除法があるという主張がある。
たとえば、「20個のリンゴを5人に均等に分配すると、おのおのに何個ずつ配ることになるか。」という問題と「20個のリンゴをおのおのに5個ずつ分配すると、何人に配れるか。」という問題では、問題の性格が異なるというのである。この流儀では、前者を等分除、後者を包含除と呼んで区別する。
除法は乗法の逆算であると考えることができるが、乗法を
[1あたりの量] × [いくつ分] = [全体の量]
と定式化すると、等分除とは1あたりの量を求める操作であり、包含除とはいくつ分を求める操作であるというのである。
しかしながら、等分除と包含除の区別、1あたりの量といくつ分の区別はあくまでも感覚的なものであり、明確に区別できるものではない。算数・数学教育において、このような曖昧で感覚的な区別を指導するのは不適切であるという主張が存在する。
20個のリンゴを5人に均等に分配する方法を考えてみよう。等分除と包含除を区別する流儀だと
[1人あたりの個数] × 5人 = 20個
となり、1あたりの量を求める等分除のようにみえる。しかしながら、以下のように考えることもできる。
リンゴをおのおのに1個ずつ配る。全員に1個ずつ配るには5個のリンゴが必要である。これを4回繰り返せば20個のリンゴを全員に均等に分配することができる。
5個 × [配る回数] = 20個
となり、いくつ分を求める包含除となる。
日常生活において均等にものを分配する場面ではどちらの方法も行なわれており、いずれも不自然な方法であるとは言えない。特に数量感覚が発達していない幼児期においては、後者の方法がふつうのやり方である場合もあり得る。
結局、20個のリンゴを「4個ずつのまとまりが5つある。」と捉えても「5個ずつのまとまりが4つある。」と捉えても、20個のリンゴがあることに変わりはないということなのである。「4個ずつのまとまりが5つあるから、5人全員に4個ずつ配ることができる。」と考えるか、「5個ずつのまとまりが4つあるから、4人全員に5個ずつ配ることができる。」と考えるかの違いにすぎない。等分除と包含除の区別は感覚的で曖昧なものである。等分除とは何か、包含除とは何かを定義することは現実には不可能である。
教育的な配慮として、乗除算の理解を深めるためには、初歩的な除法の文章題を等分除と包含除に分類して両者をまんべんなく出題することが有効であると考えられている。
しかしながら、児童に等分除と包含除の区別があるかのように指導すればかえって誤解をまねくことがあり、等分除と包含除の区別はあくまでも便宜上のものと考えるべきであるという主張がなされている。
これが加わったのは2011年5月で，中心となる編集内容の差分を見ることができます．
なのですが，この引用の直前に，「この記事の内容の信頼性について検証が求められています。」「この記事には独自研究が含まれているおそれがあります。」がついています．[http://ja.wikipedia.org/wiki/%E3%83%8E%E3%83%BC%E3%83%88:%E9%99%A4%E6%B3%95:title=ノート]の動向を，見守ることにします．
これまでに書いたこと
- 「×」から学んだこと 13.04―トランプ配り
- 水道方式入門(1961)のトランプ配り
- かけ算・わり算の8マス関係表
- トランプ配りの本質は
- 包含除先行
- 3年のわり算かけ算
- 包含除と等分除 再考
- 割り算のときにどちらを除数にしてもよいのはどうしてか
- 等分除・包含除の逆としての乗法
- 包含除と等分除
（最終更新：2013-06-09 夕方．[http://megalodon.jp/2013-0605-2357-58/d.hatena.ne.jp/takehikom/20130605/1370382764:title=前のバージョン]）
