
- 作者: 遠山啓
- 出版社/メーカー: 国土社
- 発売日: 1961
- メディア: ?
- この商品を含むブログ (17件) を見る
大学の図書館で読みました.「1961年11月1日 初版発行」「1962年1月10日 再版発行」です.銀林浩の名前は,執筆者の中にありませんでした.
この中に,「トランプ配り」の文字もありました.最初に現れる出題は,こうです.
「12枚のトランプを3人にくばると1人に何枚くばれるでしょう……12-:-3=4」
(p.242)
本書を通じて,除算記号は「-:-」となっていました.以降は「÷」に置き換えて表記します.
子どもに配る順番の挿絵も,添えられています.タテヨコ2cmくらいで,ずいぶん小さかったのですが.メモをもとに,自分なりに復元してみました.
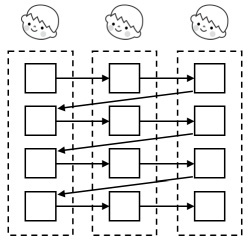
実はこれに近い図があります.[http://www.mext.go.jp/a_menu/shotou/new-cs/gengo/1300865.htm:title=言語活動を充実させる指導と事例 の算数]の中に,[http://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2011/01/12/1300865_4.pdf:title=自力解決の中で自分の表現を見直し修正する事例]というタイトルで,中身は,等分除のことを書いているものがありました.その中の,

が,似ています.とはいえ細部は違います.今回,取り上げた本では,配る対象それぞれは□で書かれており,番号は振られておらず,かわりに,配る順番が矢印で示されていました.
指導系統の中で,「トランプ配り」がどのように位置づけられているかを,書き出します.
〔等分除の指導系統〕
1 分離量÷分離量
a トランプ配り型 ※等分するということ,1当りいくつということがだれでもハッキリわかるような問題
(a) 余りなし (b) 余りあり
b キャラメルの箱入れ型 ※キャラメルを箱に入れると,1当りの量が見えなくなる。連続量の除法へのつなぎとなる。
(a) 余りなし (b) 余りあり
2 連続量÷分離量
余りなし
3 連続量÷連続量
余りなし
(pp.243-244)
当時は,「トランプ配り」は具体物を使った等分除の導入であるとと同時に,「キャラメルの箱入れ」という操作と対比される手法であったのが読み取れます.
ではこのころに,トランプ配りの等分除への適用が確立していたのかというと,そうではありませんでした.読み進めていくと,包含除にも,トランプ配りが適用されています.
最初の問題文は,次のとおり.
「12枚のトランプを1人に4枚ずつくばると何人にくばれるでしょう……12÷4=3」
(p.244)
そして〔包含除の指導系統〕の中にも,「a トランプ配り型」「b キャラメルの箱入れ型」が見られました.こちらの「トランプ配り」の右のコメントは,「※ 1あたりいくつということ,減っていく過程,おわりにいくつに分けられたかハッキリわかるような問題」となっていました.
他で読んできたこと(トランプ配りの本質はなど)と合わせると,トランプ配りは次のように大別できます.
- 除法(等分除・包含除)への適用:『水道方式入門』(1961)
- 乗法への適用:「6×4,4×6論争にひそむ意味」(遠山, 1972)
- 等分除への適用:『新版 水道方式入門』(1971),Anghileri & Johnson (1988), Greer (1992), 教科調査官の説明(2012)
等分除への適用において,図は,次の2種類を見ることができます(本日リンクした「自力解決の中で自分の表現を見直し修正する事例」「教科調査官の説明」には,両方の図があります).
- 配る対象をもとにし,一直線に配置するもの
- 配る人数をもとにし,配る対象を長方形状に配置するもの
乗法への適用の提案には,上記の遠山(1972)のほか,『おかしなおかしな数学者たち (新潮文庫)』『数の現象学 (ちくま学芸文庫)』があります.小学校の授業への活用は,なされているようには見えません*1.
私はこういったことから,トランプ配りは等分除への適用がふさわしいというのが,国内外の算数教育で認識されていると,理解しています.十分な数の文献収集・授業事例調査を行い,かつ,Webもしくは紙上で,トランプ配りの乗法への適用を提案・推奨している人は,見たことがありません.
『水道方式入門』(1961)は,驚きの連続でした.
- 乗法で《BA型》の出題が,授業(対話)例で1題,練習問題で2題,入っていました.「3年生には2組あります。どちらの組も男の子は23人です。男の子は,みんなで何人でしょう」(p.219),「②学校には867人のじどうがいます。給食費を1人から460円ずつあつめると,みんなでいくらになるでしょう」(p.239)が見られます.新版との対比で言うと,執筆者は「岡田進 東京都小台橋小学校教諭」でした.
- 筆算の順序の最後に載せた図とほぼ同型のものが,p.207で出題されていました.絵は4つあり,それぞれ形状は異なっていますが,中央の数がかけられる数(九九の「xの段」のx)で,周囲にランダムに配置された数をかける数として,かけ算の計算をするのは共通しています.
- パー書きは,見られませんでした*2.p.249では「21(枚)÷7(人)=3(枚)」「21(枚)÷3(枚)=7(人)」といった式それぞれの,「3(枚)」の上に,ルビとして「1人あたり」がついていました.
- 3×2=6と2×3=6の違いが,p.183に図つきで示されていました.
- 9+5を例として,加数分解を使った,繰り上がりのあるたし算の例が文章で記されていました(p.91).10を6と○に分け,《10に対する補数》を求めようという図---さくらんぼ計算の原型と言えるもの---が,p.95に数例,書かれていました.
(最終更新:2013-04-22 晩.トランプ配りの絵を入れました)