わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

わり算，包含除・等分除，トランプ配り (2016.05)

math reprise

目次

  • 1. かけ算とわり算，包含除と等分除
  • 2. 高学年の包含除と等分除
  • 3. 指導の歴史
  • 4. 授業例
  • 5. 海外の状況
  • 6. かけ算1つにわり算2つを見直す
  • 7. おやつの時間
  • 8. トランプ配り

本記事は2015年5月に作成したもの[Link 1t]の改訂版となります．この1年で得た情報を取り入れる一方で，重要でない情報は取り除き，参考文献・URLを末尾に集約した点が，主な変更箇所となっています．

1. かけ算とわり算，包含除と等分除

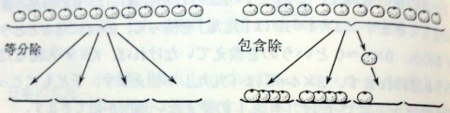
わり算は，かけ算の逆演算と考えることができます．ですが小学校では，導入時に2種類のわり算の意味が指導されています．「包含除」「等分除」と呼び，区別されます．
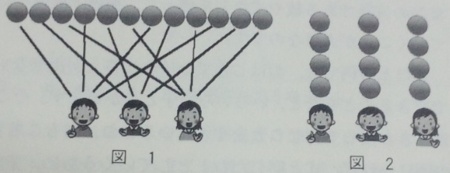
その違いは，次の図で見ることができます[Link 101t]．

横1行が，1つの場面を表し，表頭は別にして2行で構成しています．2種類の場面から共通点を探ると，「オレンジの囲みがいくつできるか」を求めるのが，包含除で，「一つのオレンジの囲みの中に，青い丸がいくつあるか」を求めるのが，等分除です．

この違いは，言葉の式を使って表すこともできます．かけ算について，「一つ分の大きさ×いくつ分＝全体の大きさ」という言葉の式（「基準量×いくつ分＝全体量」「内包量×外延量＝全体量」といった別称もあります）から話を始めます．
この関係式のもとで，「全体の大きさ」と「一つ分の大きさ」が分かっているとき，「いくつ分」を求めるには，「全体の大きさ÷一つ分の大きさ＝いくつ分」とすればいいのです．この形のわり算が，包含除です．
「全体の大きさ」と「いくつ分」が分かっているとき，「一つ分の大きさ」を求めるには，「全体の大きさ÷いくつ分＝一つ分の大きさ」とします．この形のわり算は，等分除です．
「3個ずつミカンを持った子どもが5人います。ミカンは全部で何個ですか」がかけ算の問題（式は3×5＝15）なのに対し，「15個のミカンを3個ずつ配ります。何人の子どもに配れますか」が包含除（15÷3＝5），「15個のミカンを5人に同じ数ずつ配ります。1人は何個になりますか」が等分除（15÷5＝3）となります．

包含除・等分除という言葉は，文部科学省が発行している『小学校学習指導要領解説 算数編』[Link 2]の第3学年と第5学年にも書かれています．第3学年，すなわちわり算の導入のところを，抜き出します（[Link 3]のp.110）．

ア　除法が用いられる場合とその意味
除法が用いられる具体的な場合として，大別すると次の二つがある。
一つは，ある数量がもう一方の数量の幾つ分であるかを求める場合で，包含除と呼ばれるものである。他の一つは，ある数量を等分したときにできる一つ分の大きさを求める場合で，等分除と呼ばれるものである。なお，包含除は，累減の考えに基づく除法ということもできる。例えば，12÷3の意味としては，12個のあめを１人に３個ずつ分ける場合（包含除）と３人に同じ数ずつ分ける場合（等分除）がある。
包含除と等分除を比較したとき，包含除の方が操作の仕方が容易であり，「除く」という意味に合致する。また，「割り算」という意味からすると等分除の方が分かりやすい。したがって，除法の導入に当たっては，これらの特徴を踏まえて取り扱うようにする必要がある。なお，おはじきなど具体物を操作したり，身の回りのものを取り扱ったりするなど，具体物を用いた活動などを取り入れることが大切である。
あわせて，除法には割り切れない場合があり，その場合には，余りを出すことを指導する。
イ　除法と乗法，減法の関係
除法は，乗法の逆算ともみられる。そこで，乗法と関連させて，被乗数，乗数のいずれを求める場合に当たっているかを明確にすることも大切である。包含除は3×□＝12の□を求める場合であり，等分除は，□×3＝12の□を求める場合である。また，実際に分ける場合でも，包含除も等分除と同じ仕方で分けることができることなどにも着目できるようにしていくことが大切である。そのようにして，どちらも同じ式で表すことができることが分かるようにする。

包含除と等分除の違いは，教員採用試験で問われることもあります[Link 4]．また国内外で，等分除のほうが包含除よりも難しいことが報告されています[佐藤1978] [高橋2003] [Anghileri 1988] [Link 102t]．その理由として，[高橋2003]では「整数の等分除の難しさは，分けるための単位がその場面に示されていないところにある」を指摘しています．

しかし，授業の中で用いたり，子どもたちが「包含除」「等分除」といった名称を学ぶことは，ありません．かわりに，親しみやすいネーミングを取り入れます．
よく知られているのは，「ドキドキわり算」「ニコニコわり算」です[Link 5] [Link 6]．総数が不明なときに（ただし，導入においては，あまりのないわり算を考えます），1個ずつ配っていくと，クラスの子ども全員には配れないかもしれないということで，「ドキドキ」なのに対し，3つの班に同じ数になるよう配れば，みんな公平にもらえるということで，「ニコニコ」となります．
また新潟大学教育人間科学部附属長岡小学校の取り組みでは，「ドドレ型」「ドレド型」とあります[高橋2006]．ドドレ型の例は，「12(枚)÷4(枚)＝3(袋)」で，「左辺は同じ単位で右辺は違う単位」とのこと．ドレド型は「12(枚)÷3(袋)＝4(枚)」です．
さまざまな文献で見かけた，等分除・包含除の別名を整理しておきます．

等分除 ニコニコわり算，つ割，ニワリ，分け算，ドレド型，分配，sharing
包含除 ドキドキわり算，ずつ割（づつ割），ズツワリ，取り算，ドドレ型，累減，repeated subtraction

2. 高学年の包含除と等分除

学年が上がり，小数のかけ算・わり算を指導するときにも，1つのかけ算に2種類のわり算が登場します．『小学校学習指導要領解説 算数編』の第5学年（[Link 3]のp.167）より，わり算の該当箇所を抜き出します．

小数の除法の意味
除法の意味としては，乗法の逆として割合を求める場合と，基準にする大きさを求める場合とがある。
Bを「基準にする大きさ」，Pを「割合」，Aを「割合に当たる大きさ」とすると，次のような二つの場合である。
① P＝A÷B
これは，AはBの何倍であるかを求める考えであり，除法の意味としては，Pが整数の場合には，いわゆる包含除の考えに当たる。例えば，「9メートルの赤いリボンは，1.8メートルの青いリボンの何倍になるか」という場合である。式は，9÷1.8となる。
② B＝A÷P
これは，基準にする大きさを求める考えであり，除法の意味としては，Pが整数の場合には，いわゆる等分除の考えに当たる。例えば，「2.5メートルで200円の布は，1メートルではいくらになるか」という場合である。式は，200÷2.5 となる。
これらの式は，BやPが整数の場合だけでなく，小数の場合にもそのまま当てはまると考えていくことが大切である。このとき，多くの児童にとっては，①の場合に比べ，②の方がとらえにくい。つまり，整数の場合は，P等分した一つ分の大きさを求めるという説明で，1に当たる大きさであることが理解できたが，除数が小数の場合，1に当たる大きき(基準にする大きさ)を求めているという見方に一般化するのに難しさがある。この点については，公式や言葉の式だけでなく，数直線や図などを用いたり具体的な場面に当てはめてりして分かりやすくすることが大切である。また，はじめに乗法の式に表してから，除法で求めるという考えを用いることも大切である。
(p.167)

英字について，Pをproportion（割合），AをAmount（全体量），BをBase（基準量）の頭文字と思えば，理解しやすくなります．現在の学習指導要領には記載がありませんが，割合Pを求める式P＝A÷Bを，比（または割合）の第一用法，Aを求める式A＝B×Pを第二用法，Bを求める式B＝A÷Pを第三用法と呼ぶこともあります[武藤2010]．3つを合わせて比の3用法です．第一用法は包含除，第三用法は等分除の拡張です．
包含除の拡張の式を，A÷B＝Pと書いたとき，わられる数とわる数は同種の量であり，商はそれらと異なります．このときのPについて，無次元量であるとは限らず，例えば，「200円あったら，1メートルが80円の布を何メートル買えるか」をわり算で求めると，200÷80＝2.5で，Pに対応する量は2.5メートルとなります．
また，等分除の拡張の式A÷P＝Bでは，わられる数と商が同種の量，わる数がそれらと異種の量となります．包含除はドドレ型，等分除はドレド型というのは，拡張しても成り立っています．
A，B，Pがいずれも同じ単位になるような，小学校5〜6年生向けの場面（文章題）を作ることもできます．例えば「ウサギとカメが競走を始めました．カメがスタート地点から0.2kmのところに着くと，ウサギは0.6km先にいます．ウサギとカメがそのまま進んで，ウサギがスタート地点から1kmのところに着くと，カメはスタート地点から何kmのところでしょうか」です[Link 7t]．この場合，0.2÷0.8＝0.25で求められますが，わられる数と商はカメの道のりなのに対して，わる数の0.8はウサギの道のりです．なのでこれも，等分除の拡張と見ることができます．
なお，数教協に関わってきた遠山啓や銀林浩の著書によると，「度の3用法」と「率の3用法」に分かれます．指導にあたっては，率よりも度を重視しています．率の3用法は，上とほぼ同じです．度の3用法では，1あたり量（または内包量．学習指導要領に記されている「単位量当たりの大きさ」でもあります）を求める等分除のほうが，第一用法となります．

上の引用のうち，「多くの児童にとっては，①の場合に比べ，②の方がとらえにくい」について，掘り下げてみます．番号ではなく言葉にすると，「包含除（の拡張）よりも等分除（の拡張）の方がとらえにくい」となります．
このことについて，平成19年度（2007年度）から毎年4月に行われている，全国学力・学習状況調査（全国学力テスト）[Link 8] から，いくつか出題例を見ていきます．なお，全国学力テストの算数では第5学年までの学習事項をもとに，出題されますので，整数および小数の加減乗除はすべて含まれますが，分数については加減算と，乗数・除数が整数の場合に限られ，「×分数」や「÷分数」は出てきません．
平成27年度（2015年度）の算数B問題で，「せんざいを買います。家で使っているせんざいが，20%増量で売られていました。増量後のせんざいの量は480mLです。増量前のせんざいの量は何mLですか。求める式と答えを書きましょう」が出題されました．式は例えば480÷1.2で，答えは400mLです．なのですがこの正解率は，13.4%と低くなりました（480×0.8や480÷0.2といった誤答のほうが，多くなっています）．「20%増量」を「増量前の1.2倍」と置き換えることができれば，わり算の式は等分除の拡張です．
平成24年度（2012年度）の算数A問題では，「犬を飼っている人は8人です。この8人は，学級全体の人数の25%にあたります。学級全体の人数は何人ですか。求める式と答を書きましょう」が円グラフとともに示されています[Link 9t]．そこでは「8÷0.25」だけでなく「8×4」も，◎による正答となっています．このわり算の式もまた，等分除の拡張です．
わられる数とわる数に注意して，立式する問題には，平成22年度（2010年度）の算数A問題の「8mの重さが4kgの棒があります。この棒の1mの重さは何kgですか。求める式と答えを書きましょう」があります．正解となる式は4÷8です．8÷4は誤答であり，「(整数)÷(整数) の除法では，被除数の方が除数より大きくなると考えている」という分析も書かれています（この問題に解答した児童らが，3年後の中学A問題で「a[m]の重さがb[g]の針金があります。この針金1[m]の重さは何[g]ですか。a，bを用いた式で表しなさい」を解答しています[Link 10t]）．「8m」も「4kg」も，一見すると，割合ではありませんが，「8mの棒を1mにすると…」と考えると，8が割合とつながってきます．また前述の「わられる数と商が同種の量，わる数がそれらと異種の量」からも，等分除の拡張なのが分かります．

以上をもとに，誤答の典型的な状況を整理してみます．
高学年になったら，割合にあたるPが1よりも小さいとき，A÷Pの式が正解となる文章題で，A×Pとやってしまいがちです．また上記の，棒の重さの問題は，A÷Pが正解，P÷Aは誤答という事例です．いずれも，等分除の拡張に当たります．
包含除の拡張で，間違えるのは，A÷Bと書くべきところで，A×B，B×A，B÷Aとしてしまうケースが考えられます．ですが，面積を求めるのではない状況で，同種の2つの量を，かけるのには抵抗が出ますし，割合を求める場面では，Bに当たる数量（基準量）を見つけやすいのではないかと考えられます．
結局のところ，等分除の拡張のほうが，子どもたちは間違えやすく，外在的評価[Link 11t]のテスト問題でもよく用いられてきたわけです．

3. 指導の歴史

包含除・等分除という言葉は，昭和初期の書籍からも見ることができます．[木村1936]のp.23には，次のように書かれています．

脚注の「包含除の本質は累減にあると見ることが出来る．」が，大事なところです．
この前後では，a×b＝cからaまたはbを求めるのを割算と称し，いくつかの用語を定義しています．そして「次の二つの場合」とし，(1)が上記の包含除で，例文を文字にすると，「12銭は4銭の幾倍か（幾つ含むか）」です．次のページに進んで，(2)が等分除です．等分除の例文は，「12銭は幾銭を4倍したものか．（四つに等分するとその一つ分は幾らか）」です．そのあと，乗法の交換法則を理由に挙げ，「積と一因数を知って他の一因数を求めるものである」と，まとめています．

昭和50年代に移りますと，[新算研2011]は，新算数教育研究会の機関誌「新しい算数研究」から論説を精選し，テーマごとに章分けするとともに解説を入れています．第4章が「除法の意味」となっており，1978〜1980年（1件だけ，1985年のものがあります）の論説や研究事例を読むことができます．
章のはじめの解説(pp.130-131)では，包含除（から指導を始めること）が優勢のように見えます．“配り方”についてもp.145 [長田1978]で挙げられています．「包含除の場合は，同数累減という操作で処理できる」「被乗数先唱で九九を唱えれば，除数を先唱して商を見つけることになる」といった理由を挙げ，包含除から導入することの分かりやすさを指摘しています．
ここでなぜ，包含除のほうが分かりやすいのか，そして「被乗数先唱」が出てくるのかを，ミカンの問題を使って確認します．「15個のミカンを5個ずつ配ります。何人の子どもに配れますか」（包含除）に対して，わり算を知らない（または除法を乗法と関連づける活動として）状況で表したかけ算の式，5×□＝15から，□を求めるのは九九の五の段が使えます．すなわち「五一が5，五二10，五三15」として，□は3となります．一方，「15個のミカンを5人に同じ数ずつ配ります。1人は何個になりますか」（等分除）に対する式，□×5＝15から，□を求めるのは，何の段を使えばいいか分からない分，手間がかかるというわけです．なお，5×3＝15を「五三15」というのが被乗数先唱，それに対し3×5＝15を「五三15」というのが乗数先唱です．
とはいえ，[新算研2011]には，等分除を先，包含除を後とする指導法も入っていまして，pp.156-159にあります[正木1980]．その根拠として「等分するという生活経験が子どもには多いし，問題場面の理解が容易」を挙げています．被乗数先唱・乗数先唱の件は，「かけ算の交換則を認め，自在に使っている子どもだから」により，うまくいくとしています．
優劣ではないのですが，黒表紙時代の考え方が書かれているものが興味深かったので，p.137より抜き書きします[杉山政1978]．

しかも，除法における演算決定の困難性を次のように，加減乗と異なる二義性にあると説く．

整数四則算法のうち，最も児童の了解に困難を訴ふるのは除法である．(略)即ち，等分・包含といふ派生的の二義的観念が算法の本質をなして居る．この二義性が児童を昏迷せしむる所以である．

かくして「算法は四則にあらずして五則なり」などという見解も流布された．また「なぜ割るのか」の判断基準を包含・等分の意味に求めることの重要性が指摘され，等分を「つ割」，包含を「ずつ割」などと称して，意味の徹底を図ろうとする試みさえ出現するにいたった．(略)

引用の中の引用に出現する「二義的観念」や，その後の「五則」などについては，そこで挙げられた出典と異なりますが，[水木1923]のp.128でも見ることができます．
外国の教科書に基づく論説も，[新算研2011]に収録されています．[杉山吉1978]には，先頭から2番目の段落に，「包含除，あるいは同数累減といった立場で指導を展開している教科書が多い」とあります．それと対比する形で，最初の段落は日本の（昭和50年代前半あたりの）算数指導が述べられており，「ほとんど同時にとりあげる」となっています．

現在はというと，算数・数学教育に関する理論的・実践的研究の集大成として出版された[日数教2010]を見ることにします．
第3章§2（演算の意味・手続き）の中で，除法の意味づけについて記されています．「除法は，乗法を割合で意味づけた場合，基準量を求める場合と割合を求める場合の2つがある。それを別々にせず，乗法の逆演算ということで意味づけることもある」(p.74)とあり，これのみを見れば両論併記ですが，以降では，別々にしない意味づけでの指導方法が見られず，直後の段落には「等分除」と「包含除」が，そして次ページの結論に関わる中に「整数÷整数の包含除」が書かれています，そういったことから，主流となる考え方・教え方は「包含除と等分除をともに学習させること」「包含除を主とすべきこと」なのが読み取れます．
包含除と等分除の区別を知っておくのには，いくつか意義があります．一つは，子どもたちが問題に取り組むときに，「あ，これはわり算だ!」と判断できるようになることです．大人の立場でも，数や量の構成（ものの見方）をより豊かにすることができます．
加えて，現在の日本の教育では「言語活動」，算数においては「算数的活動」のウエイトが高まっています．そうしたとき，ある出題（文章題，場面）に対して，子どもたちが答え（個数，人数など）だけ，あるいは式と答えだけを書くのでは不十分であり，その判断・根拠を説明できるようになることまでが期待されています．包含除と等分除の区別は，演算決定の根拠をより明確にし，算数（数学）と日本語を結びつけたコミュニケーションを図りやすくするのに寄与すると言えそうです．

4. 授業例

比較的最近の指導例を2つ，取り上げます．[相馬2011]のp.85では，次のような，わり算の問題と授業例が紹介されています．

文字にしておきます．

第3学年　D　数量関係
わり算　わり算が用いられる場面
問題43
12このクッキーを絵のように分けました。
式にあらわすと，どちらが正しいでしょうか。
　　ア　12÷4
　　イ　12÷3

どちらが正しいか予想させると，「アが正しい」，「イが正しい」，「どちらも正しい」に分かれます．それぞれの考えを説明し合う中で，クッキーの置く手順の違いや，「○人に分ける」や「○個ずつ分ける」など，分け方の違いを確認していきます．そして教科書を用いて「わり算は，同じ絵でも式が違う場合がある」ことをまとめる，としています．
というわけで，問題文は「どちらが正しいでしょうか」ですが，結論は「どちらも正解」という授業でした．
その次のページでは，「リボンの長さを5倍すると30mになります。リボンの長さは□mです。」の式に「ア　30×5＝□」「イ　5×□＝30」「ウ　□×5＝30」を提示しています．そしてアとイはおかしく，ウが正しい，と展開します．これも第3学年でして，「□を使ったかけ算」の問題と授業例です．

2011年6月4日にNew Education Expoで実施された公開授業も，刺激的な内容です．基調講演者が報告を書いています[Link 12]．筑波大学附属小学校の田中博史氏が，3年生の算数，等分除の導入の授業を行いました．
報告の中ごろに，「かけ算の順序」を意識したディベートが出てきます．

ぼくが心を奪われたのは、アメを4人に等分した後のこと。
「では、これを計算でできるかな？」と先生。
生徒たちがノートに書いたものを前面で紹介し、賛否を問います。
ア　４×３
イ　３×４
ウ　どっちもいい
エ　どっちもだめ
さあ。すると生徒たちはワアワア手を挙げてディベートです。
「アがいい。4人がいて、それで3個ずつ。」「3個のアメを4人に分けるからイ。」「３×４だと最初から3個って解ってるってことじゃん。」「４×３だって最初から3個って解ってるから、どっちもだめ。」「４×１個を3回やるってことだから、ア。」
各陣営が大変な意見の応酬で。すると、後ろに座ってた300人の業界人や先生たちもザワザワと議論を始めました。
なるほど、この授業のヘソは電子黒板やデジタル教材でのわかりやすい視覚効果ではなくて、そこからスタートした、定まらない答えをみんなで考える、この時間なのですね。
授業全体の7割の時間がこのディベートに当てられています。

「４×１個を3回やるってこと」はトランプ配りを思わせます．
算数のディベートはというと，次のようにして収束させていました．

さて、目の前の公開授業では、アが優勢になり始めました。
が、おさまりがつきません。
すると先生、今度は別の子が書いた式を前で紹介。
□×４＝１２
なるほど、これで納得。
というところでチャイム。授業終了。

田中先生は，授業を受ける子どもたち，そして参観する人々のことをよく考慮して，授業を展開したのが伝わってきます．みんな先生の手のひらの上で踊らされた，と言ってもいいのかもしれません．

5. 海外の状況

海外の包含除・等分除を見ていくことにします．ちょうど100年前に米国で出版された書籍[Klapper 1916]にも，"Quotition and Partition"と題して，それらの違いが解説されています(p.202)．私訳は以下の通りです[Link 13t]．

等分除と包含除
　わり算には2種類があると考えられる．与えられた全体（の数や量）を，多数のグループに分ける状況を仮定しよう．各グループの1つ分の数を求める必要があるかもしれない．16セントを多くの子どもたちに分ける場合，1人につき2セントずつ受け取るとすれば，2セントを受け取る子どもの人数を求めることになる．しかし16セントを8人の子どもたちに（等しく）配るなら，それぞれの子どもに与えるのが何セントかを求める必要がある．
これら2種類のわり算は，それぞれ包含除，等分除として知られている．
　包含除では，（同じ数量になる）グループの数を求める．被除数と除数は同じ種類の量となる．被除数と商は異なる種類の量となる．
　等分除では，（同じ数量になる）グループの，1つ分の数量を求める．被除数と商は同じ種類の量となる．除数は抽象数となる．
　等分除は，「15ドルの\frac15」といった，ある数（量）の決まった分数部分（割合）を求めることと密接に関係する．包含除は，「3ドルは15ドルの何倍」のように，ある数（量）が他方の何倍かを求めることと密接に関係する．
　これら2種類のわり算について，教師は理解して授業においては様々な例とともに求め方を教えるべきである．ただしそれらの用語を子どもたちに教えるべきではない．

最後の文まで含めて，内容は，現在の「等分除」「包含除」と同じと言っていいでしょう．なお，「除数は抽象数となる．」は，原文では"the number in the divisor is abstract."です．「16セントを8人の子どもたちに（等しく）配る」を例えば「16セントを8つの袋に（同額になるよう）分けて入れる」に変えても，1つ分は16÷8＝2で2セントとなりますので，除数の量のうち「人」「袋」を取り除き，「2」とするのが抽象数です．それに対し，セントを他の単位に置き換えると，答えの単位もそれに伴い変わってきます．

「現代化」より後に出た，海外文献を3つ，手短に紹介します．まず[Vergnaud 1983]では，"first-type division"，"second-type division"という名称を挙げています．それぞれ，等分除と包含除に対応します．複比例に対する"first-type division"，"second-type division"も議論されており，それについては後述します．
[Fischbein 1985]では，イタリアの第5・7・9学年の生徒623名を対象として実施したかけ算・わり算の文章題テストが報告されています．正解となるわり算の式には，"(partitive)"と"(quotative)"のいずれかが添えられていて，テストを企画する段階から，等分除，包含除というわり算の2種類の意味が考慮されていたことがうかがえます．数の対象は整数と小数で，分数は出現しません．わられる数・わる数ともに整数でわる数の方が大きくなる場面や，わる数が1より小さい場面で，正解率が低くなるのも，一覧表を通じて知ることができます．
[Greer 1992]では，〈乗数と被乗数が区別される文脈〉だと1つのかけ算に2種類のわり算，〈乗数と被乗数を区別しない文脈〉だと1つのかけ算に1種類のわり算として，乗除の関係が表になっています[Link 14t]．

英語で読める，新しい指導の体系として，米国のCommon Core State Standards（共通基礎基準）があります．かけ算とわり算は，3年で学習します．[Link 15]に記載された，CCSS.Math.Content.3.OA.A.1とCCSS.Math.Content.3.OA.A.2を見比べると，かけ算は1種類なのに対してわり算は2種類であること，そして等分除と包含除を区別して（いずれもわり算で求められる事例として）扱うべきことを示唆しています．
またこの基準では付録として，かけ算とわり算の問題および式が，表になっています[Link 16]．表の中段，"Area example"にある，"18 ÷ 3 = ?"によって求める問題を訳すと「ある長方形の面積は18㎠である．1つの辺の長さが3cmのとき，もう1つの辺の長さはいくらか」で，"18 ÷ 6 = ?"によって求める問題は，3を6に置き換えただけです．それ以外の場面では，2種類のわり算の文がそれぞれ異なっています．面積にも，1つのかけ算に2つのわり算という考え方を適用した，といったところでしょうか．
歴史的にも国際的にも，初等教育における除法には，2種類の意味づけがなされてきたと言っていいでしょう．

6. かけ算1つにわり算2つを見直す

はじめの節で，「一つ分の大きさ×いくつ分＝全体の大きさ」という言葉の式を用いて，1つのかけ算に対して2つのわり算の式，具体的には「全体の大きさ÷一つ分の大きさ＝いくつ分」と「全体の大きさ÷いくつ分＝一つ分の大きさ」を得ていました．
しかしここまで書いてきた中に，「一つ分の大きさ×いくつ分＝全体の大きさ」に基づいていないかけ算を，ちらほら見かけました．そこでは，わり算の意味づけも異なってきます．
例えば，「縦の長さ×横の長さ＝長方形の面積」について，「長方形の面積÷縦の長さ＝横の長さ」と「長方形の面積÷横の長さ＝縦の長さ」という式を得ることはできますが，これらは実質的に同じ式となります．〈乗数と被乗数を区別しない文脈〉では，1つのかけ算の式に対応するわり算の式は，実質的に，1つです．
面積のかけ算と「掛け算の順序交換」について，2010年の「熟議」に見られるコメント[Link 17]が興味深いものとなっています．全体としては算数教育を批判するスタンスですが，順序を交換して良い掛け算と，そうでない掛け算の存在を指摘しています．
面積のわり算は，『小学校学習指導要領解説 算数編』の第4学年には（[Link 3]のp.159）．「そして，（縦）と（横）から（面積）が求められるという見方に加えて，（面積）と（横）から（縦）を求めることもできるというような，公式の見方ができるようにすることも大切である。」と記されています．
「（面積）と（縦）から（横）を求める必要はないのか?」と問われれば，「『面積＝縦×横』は，『一つ分の大きさ×いくつ分＝全体の大きさ』とは異なる種類のかけ算なんだよ」と答えればいいのです．
[銀林1975]では，除法の意味として「A. 1あたり量の第1用法」「B. 1あたり量の第3用法」「C. 直積型の逆算」「D. 包含除」「E. 等分除」の5種類を挙げています（名称は異なりますが，これと同様の5種類の除法を，[Vergnaud 1983]に見ることができます）．DとEは，「倍」の逆算です．Cについては，「xy＝zにおいて，2つの量xとyはまったく対等だから，その逆演算は1つしかない」(p.116)としています．

長方形の面積は，縦の長さと横の長さに比例します．算数・数学教育においては，2つの量xおよびyについて，xの値を2倍，3倍，…すれば，それに伴ってyの値も2倍，3倍…になるとき，「xとyは比例の関係にある」「yはxに比例する」と言います[Link 18t]．これを拡張させて，3つの量x，yおよびzについて，yを固定してxを2倍，3倍，…すれば，それに伴ってzも2倍，3倍…になり，xを固定してyを2倍，3倍，…すれば，それに伴ってzも2倍，3倍…になるとき，「x，yとzは複比例の関係にある」「zはxおよびyに複比例する」と言います．複比例では，2種類のわり算が出てきます[Link 13t]．
[Vergnaud 1983]に載っている，multiple proportion（複比例）のfirst-type divisionとsecond-type divisionについて，和訳すると「ある農家が，牛乳の平均（1日あたりの）生産量を求めたい．牛は17頭いて，180日間に70340リットルを生産した．平均生産量はいくらか」と「あるスカウトキャンプには500kgのシリアル（食品）がある．1人が1週間で0.6kgを消費する．236人いるとき，シリアルは何週間もつか」です．
それぞれ，最も大きい数を他の2数で割れば，答えが出てきますが，単位の扱いが異なっています．実際，前者の文章題では70340[kg]÷180[日]÷17[頭]≒23[kg/頭・日]と表せるのに対し，後者は500[kg]÷0.6[kg/人・週]÷236[人]≒3.5[週]となります．
ここで「23[kg/頭・日]」や「0.6[kg/人・週]」は，[銀林1975]に書かれている「複内包量」です．この用語を使って違いを説明するなら，前者の例題は複内包量を求めるもので，等分除を複比例の場面に適用したと見ることができるのに対し，後者は，除数の1つに複内包量が入っており，異なる演算となっています．包含除に近いものの，少し異なっています．500[kg]÷0.6[kg/人・週]÷236[人]≒3.5[週]の式を，500[kg]÷0.6[kg/人・週]≒833[人・週]と833[人・週]÷236[人]≒3.5[週]に分けて考えます．そうすると，前者は包含除の複比例への適用となり，後者は長方形の面積について「縦の長さ＝面積÷横の長さ」となるのと同様に，量の積に基づく除法となります．なお，[Vergnaud 1983]では「複比例」より前に「量の積」を取り上げています．
複比例のわり算を，文字を使って整理しておきます．まず，zがxおよびyに複比例するというのは，z＝axyという式で表せます．ここでaは複比例定数で，上述の複内包量が対応します（x，y，zは一般にそれぞれ異なる外延量です）．これはかけ算の式ですが，zとxとyの値が既知で，aの値を（a＝z÷x÷y＝z÷（x×y）によって）求めるわり算と，zとaとxの値が既知で，yの値を（y＝z÷a÷x＝z÷（a×x）によって）求めるわり算の2種類に，区別することができます．ここで，zとaとyの値が既知で，xの値を求めるのは，後者と実質的に同じです．複比例の式でaを1とすると，面積や物理量の計算に活用できますし，xyを1つの文字に置き換えると，「xとyの積は，zに比例する」という関係になります．
複比例はいろいろな見方ができて楽しいのですが，小学校の算数の6年で，「比例」を数量関係の集大成としているところからすると，残念ながら，複比例の小学校での指導は，現実的とは言えません．なお，複比例を含む「3口のかけ算」については，[Link 19t] [Link 20t]で整理を試みてきました．

　4人の姉妹がいました。アヤコ，カナコ，サワコ，タダコという名前です。
　ある日，アヤコはお友達と遊びに行って，家にいません。お父さんが，カナコ，サワコ，タダコの3人を呼んで，言いました。
「おやつの時間だね。みんなでおいしいのを食べるか」
　子どもたちは，喜びました。
「ちょうど，『ひとくちみかんゼリー』をもらったところで，仏様にお供えしているから，取ってこよう」
「いくつ？」
「そうだなあ。ゼリーは確か，15個あったぞ」
　子どもたちは，またも喜びました。
「ちょうどいい。わり算の問題だぞ。15個を3人で同じ数ずつ分けたら，1人いくつかな？」
　子どもたちは，声をそろえて言いました。
「15÷3＝5！」
「そのとおりだ。ではゼリーを取ってくるよ」
　お父さんが，ゼリーを持って，お母さんといっしょに，カナコ，サワコ，タダコのところに戻りました。
「ほら，やるぞ」
　子どもたちは，ますます喜びました。
「そら。1個目は，カナコ，サワコ，タダコ，お母さん，お父さん。2個目は，カナコ，サワコ，タダコ，お母さん，お父さん。そして　3個目は，カナコ，サワコ，タダコ，お母さん，お父さん」
「あれっ？」
「みんな，3個ずつあるよな？」
「お父さん，おかしいよ」
「どうした？」
「さっき，1人5個って言ったじゃない！」
「パパは言ってないよ」
「言ったよ！」
「そうか？ わり算の問題だぞ。15個あって，3個ずつで，何人に分けられるかな？」
　子どもたちは，声をそろえて言いました。
「15÷3＝5！ あれ？」
「そうだよな。今，おうちには5人いるんだから，3個ずつ5人で，ゼリーはちょうど15個だ。めでたし，めでたし。はい，お父さんの分は，ごちそうさま。お前たちも，早く食べるんだよ」
「お父さん，ぜったいおかしいよ！」

8. トランプ配り

「一つ分の大きさ×いくつ分＝全体の大きさ」に立ち返ります．この式（乗法）と，包含除・等分除に対して，トランプ配りを用いて視覚化・手順化を試みている事例が豊富にあります．そこで以下のとおり，名称をつけておきます．

  • トランプ配りの乗法への適用：トランプを配る操作により，「一つ分の大きさ×いくつ分＝全体の大きさ」を視覚化・手順化すること
  • トランプ配りの包含除への適用：トランプを配る操作により，「全体の大きさ÷一つ分の大きさ＝いくつ分」を視覚化・手順化すること
  • トランプ配りの等分除への適用：トランプを配る操作により，「全体の大きさ÷いくつ分＝一つ分の大きさ」を視覚化・手順化すること

文脈から明らかなときは「トランプ配りの」を取り除きます．この3種類の中で，事例として最も多いのは，等分除への適用です．しかし乗法への適用，包含除への適用についても，見るべき記述があります．
トランプ配りの乗法への適用を示したので有名なのは，遠山啓です．「6×4，4×6論争にひそむ意味」と題する記事が1972年の科学朝日に掲載され，[遠山1978]から読むことができます．同年1月，朝日新聞に掲載された論争（テスト問題は「6人のこどもに，1人4こずつみかんをあたえたい．みかんはいくつあればよいでしょうか」）に対し，次のように記しています(p.116)．

ミカンを配るのに，トランプを配るときのやり方で配ると，1回分が6こ，これを4回くばるのだから，それを思い浮かべる子どもは，むしろ，
6×4＝24
という方式をたてるほうが合理的だといえる。

遠山と親交のあった数学者による著書，具体的には[森2009]（pp.67-68; 次元を異にする3種の乗法）および[矢野1984]（pp.121-124; 遠山啓 - カード式配り型）にも，同様の手法が書かれています．
遠山が指摘したより前には，[中野1957](pp.151-152)に，また比較的最近のものだと[齋藤2013](pp.9-10)にも，トランプ配りをかけ算に適用できる事例を見ることができます．また戦前に，高木貞治も，被乗数と乗数を合わせて因数と定義するのに先だち，記述しています[高木1911]．文章は次の通りです（[Link 22]に記載のものを一部修正）．

例へば，24人に16個づつの物を与ふるには16×24だけの物がいるべし。さて24人に1個ずつを与ふるには24個の物がいり，16回かようにするときは，24×16だけの物がいる。
此例によりて，16に24を掛けても，又は24に16を掛けても，積は同じことなるを知るべし。

トランプ配りの包含除への適用は，[遠山1961]に載っています．そこでは，〔包含除の指導系統〕の中に，「a トランプ配り型」「b キャラメルの箱入れ型」が入っています(p.244)．「トランプ配り」の右には，「※ 1あたりいくつということ，減っていく過程，おわりにいくつに分けられたかハッキリわかるような問題」というコメントがついています．
とはいうものの，同書の〔等分除の指導系統〕(p.233)と合わせて，見ておく必要があります．それは，次のようになっています．

〔等分除の指導系統〕
1 分離量÷分離量
　a トランプ配り型　※等分するということ，1当りいくつということがだれでもハッキリわかるような問題
　　(a) 余りなし　(b) 余りあり
　b キャラメルの箱入れ型　※キャラメルを箱に入れると，1当りの量が見えなくなる。連続量の除法へのつなぎとなる。
　　(a) 余りなし　(b) 余りあり
2 連続量÷分離量
　余りなし
3 連続量÷連続量
　余りなし
(pp.243-244)

当時は，「トランプ配り」は具体物を使った等分除の導入であるとと同時に，「キャラメルの箱入れ」という操作と対比される手法であったのが読み取れます．そして，それらの対比は包含除でもつくることができる，ということです．
なお，1971年の新版[遠山1971]では，トランプ配りは等分除への適用のみとなっています．
それでは，最も多い，トランプ配りの等分除の事例を見ていきましょう．

■[遠山1961]
(p.242，再現)

■[遠山1972]
(p.88)
(p.89)

■[文部省1986]

4.1.2 除法の素地
先に述べた乗法の素地となるような経験は，見方を変えれば，いずれも除法の素地にもなっている。例えば，数えることに関しては，「8個のみかんは，2個ずつまとめて数えると4回になる。」などという見方ができるようにする（図1）。これはまた，減法で表すと，8−2−2−2−2で数え終えたことになる。
また，分配を，計算とは別に，実際にそうさせることもある。例えば，「8個のみかんを4人に分けるにはどうしたらよいだろう。」などという場面を考え，各人に1個ずつ配り，まだ余りがあったらまた1個ずつ配るという活動をさせる。
(pp.144-145)

（図1，再現）

■[Anghileri 1988]
(p.147)
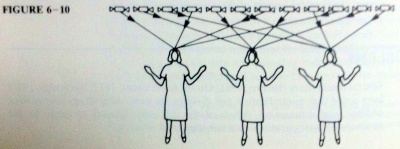(p.156)
(p.160)

■[Greer 1992]
（p.281;）

■[水戸部2012]
（p.71;）

■[相馬2011]
（p.85）

■[田中2013]
（pp.57-58）

■[Link 23]

トランプ配りの等分除への適用は，数が多いだけでなく，英語の文献でも見ることができます．また，分ける対象を一列に並べているものと，アレイ図で表現するものが見られます．
[遠山1972]や[遠山2009]では，トランプ配りによって，分離量においては等分除・包含除の意味の転換が可能であることが述べられています．あるいはトランプ配りを介して，等分除・包含除を同等視できる，もっというと，それを根拠として，わり算は2種類ではなくて1種類なのだ，と主張することもできそうです．
ただ，それは一時期の主張であったと認識すべきでしょう．トランプ配りは等分除を累減の操作により可視化・手順化したものであること，言い換えると，等分除は累減（包含除）に帰着されるのが，国内外の書籍・事例を通じて読み取れ，遠山が示したことよりも，詳細な見方となっています．

「等分除・包含除」は，わり算で求められる場面の分類です．それに対し，「数巡方略・一巡方略」[山名2002]や"dealing-out" [Greer 1992]は方略の分類となります．「sharing（分配）・repeated subtraction（累減）」，「ニコニコわり算・ドキドキわり算」などは，場面と方略の中間的な存在となっています．

参考文献

以下はWebの情報です．番号のあとに「t」がついているものは，筆者が作成しました．

（最終更新：2016-05-30 朝）