はてブありがとうございます.
id:bn2islanderさん,id:nemobaさん,id:u4mgさん,ポジコメ感謝です.
批判が多いのは,承知の上です.いくつかコメントを取り出して,思ったことを書いておきます.
テスト
id:Ayrtonism 問題は、その「意味が違う」とやらを根拠にテストで×をつけることなんだけど。できる子は、かけ算を習った次の瞬間には交換法則が成り立つことを“理解”してる。それをわざわざ混沌に突き落すことに何の価値が?
id:hiruhikoando 算数なのに国語の問題になっているのがねえ。受験の悪問にありがちだからこそとっとと追い出したいのだが。
教育現場では「テスト」ではなく「評価」に関心が向けられています.田中耕治『教育評価』によると,教育評価は,ともすれば解答者を値踏みして勉強や発達をあきらめさせる道具から,子どもたちに質的に高い学力を保証し,教育実践への参加を促す装置へと転換してとのこと.昨年末に「計算の意味の理解」の調査における一考察を書いたので,ご覧ください.
なお,「かけ算の順序」が中学なんかの受験で問われたのを,見たことはありません.
東大附属中学の入試で,問題説明の中に「110円×8m^3=880円」と書かれていたそうですが(九九する究めるハックする),答案に,単位付きとか順序まで注意したかけ算の式を要求したわけではなさそうです.この件,小学校だったら「110×8=880」と式にするところ,「110円×8m^3=880円」でも分かってくれるかな,と少し応用力を試したのかなあと思っています.
国語
id:jtw 国語の時間でやってくれませんかね。読み替える応用力を奪う教育にしか思えません。
id:kent013 式を答えとして書かせるから論争になるんじゃないかなぁ。式を導いた理由を答えとして書かせればいいんじゃないの?式を答えとして求めていない問題の正解が式になってるのが問題なのか。日本語難しい。
これは,算数の問題だと思いますよ.再度リンクですが,「計算の意味の理解」の調査における一考察で出題事例を取り上げています.
授業でどうなっているのかだったら,以下をご覧になって,お選びください.
式の意味
id:hidematu 意味のないものに意味を付与するというのは呪術的。少なくとも科学的ではない。
id:norinorisan42 意図としては簡単な式の段階から求める式の意味するところにこだわる必要性を学ばせる、といったところか。ならばそういったきちんとした理屈を持って説明すべきで、丁寧に説明せずに×というのはきっと、違う
id:morita_non 数式に意味を導入するなんて、この算数という学問は、数学よりも上位にあるんですね。分からないのも納得。
id:amamiya1224 だからさ、式に意味を求めるのが間違ってんだって。
id:seven-teen-rocket 数式に意味を求めるなら、「算数」という教科名をやめて「数学」にするべき。算数はしょせん算数やろうもん。
式の意味は,2008年の学習指導要領改訂から,「算数的活動の充実」によって,ますます重要になっています.
先生が黒板に,問題を書きます.子どもたちはノートに書き,式を作って,答えを出します.先生が指名して,ある子どもが黒板に,答えを書きます.
それで,先生は他の子を指名します.なぜそのように書いたのかを,言うのです.指名された子は,自分のことばっかり考えていては,説明ができません.黒板に書いた子の立場にたって,表現することが求められます.
この流れにおいて,先生に指名権がありますから,わざと,間違った式の子に書かせて,議論することだってあるでしょう.バツを生かす教育です.2円あまるの話が,個人的にはお気に入りです.
式の意味ではなく,かけ算の意味のことだったら…
被加数・加数の順序
- 乗法に〈乗数と被乗数が区別される文脈〉と〈乗数と被乗数を区別しない文脈〉があるのと同様に,加法にも〈加数と被加数が区別される文脈〉と〈加数と被加数を区別しない文脈〉が考えられます.
- 〈加数と被加数が区別される文脈〉は「増加」(または「添加」),〈加数と被加数を区別しない文脈〉は「合併」という名称で,算数教育の場で十分に普及しています.
- ただし,加法は〈加数と被加数を区別しない文脈〉から先に学習するのが良いとされています.乗法が〈乗数と被乗数が区別される文脈〉から先なのと対照的です.
Q: かけ算は面積で考えればいいのでは?
なぜコメント凍結
A: その考え方では,3キロワット(kW)が2時間(h)で6キロワット時(kWh),だけれど3個入りの袋が2袋だと6個になり,「6個袋」ではないのはなぜか,説明に苦労することになりそうで,賛成できません.
Q: 3個入りの袋が2袋は,3個/袋×2袋=6個じゃないの?
A: その考え方で大丈夫ですよ.面積とまた別の,かけ算の構造があるという次第です.「倍」「比例関係」「面積(直積)」という3つの分類のしかたが,国内外の本で記されています.
絵を描かせるのは
id:pazl それなら最初から回答を絵で描かせればいいんじゃね?それから、●印の線の区切り方も横でもいいじゃん?問題は、概念の習得の判断として現状の問題と正答が不適切なことだと思います。
id:t-tanaka 単位で表現すれば「(N/U) × U = N」という公式を習っているのであって,その公式を適用する練習をしているのだ,という主張。/ id:n46 問題図の台形が斜辺を下に描いてあったら,どう答えるのが正解なのだろうか?
図を描かせて,問題文(場面,言葉)と図と式の関係を見ることについては,3度目になりますが,「計算の意味の理解」の調査における一考察で検討してみました.
「(N/U) × U = N」は,どの教科書も採用していないと思います.「1あたり」に基づく,先生方の指導法だと思います.
わざと斜めに配置した図形の面積の件は,ななめをご覧ください.
正しい式
id:ktasaka 2013年版の割にはかなり周回遅れな内容。すでに議題は「正しい定義の式ってなによ(つまりこのブログの中でさらっと流しちゃった部分ね)」になっているのに。誰も順番に意味がないなんて言ってないよ。
id:iww 『「正しい式」の定義次第でしょう』 正しい式の定義がグラグラ揺れるような教育はいかんと思うなぁ
何が正しいかは,我々が決められるという話ではないのが,実情ですね.
一つ,手がかりになりそうな記述があります.全国学力テストの「乗数と被乗数を入れ替えた式なども許容する。」です.高学年のかけ算の指導と正誤判定で詳しく書いています.高学年でも「正解はこれ」というのはあるけれど,5年までで学習することを踏まえ,そこまで厳密にしなくてもいいだろう,ということだと理解しています.
なお,低学年と高学年の違いは,『小学校指導法 算数』でも書かれています.そのほか,「かけ算の順序」を学ぶための本など - Togetter経由で,http://t.co/Z2VC45Z4を見たとき,ある文章題の式に「A 4こ×45=180こ」と「B 45×4=180」の2種類があり,AもBも正解とするのが,2年生ではなく「四年生の指導例」となっているのも,目を引きます.
その他
id:shidho 天動説について書かれた過去の文献を羅列して「だから天動説は正しいんです」って言ってる感じ。/ id:bn2islander より正確には「太陽が地球を回っていると言う表現がこんなにあるから天動説は正しい」かと。
何をもって天動説・地動説とするかも気になるけれど,ともあれ私のかけ算に関する認識は次のとおり(「倍」と「積」から学んだこと).
- 乗法の意味は「被乗数と乗数のペア(倍の乗法,倍指向)」と「2つの因数(積の乗法,積指向)」に大別される
- 論理的には優劣なし(倍指向から積の乗法が計算できるし,積指向から倍の乗法が計算できる)
- 教師らの観察では,積指向に基づく乗法の指導はうまくいかない.
テストやマルバツについては,「教育評価」をどれだけ理解しているか次第だと思っています.
id:zona4203 順序で意味が変わるのはわかるんだが、式として(容量)×(容器の数)の順にする必要性はどこにあるのか
慣習です.戦前にさかのぼって,事例を見ることができます.
『「小学算術」の研究』は緑表紙教科書編纂のことを記した本ですが,「5円の色紙を8枚」「3を4倍する」という言い方,「5円×8」という式が例示されています(筆算の順序).他書には「3銭の鉛筆2本」を「3銭の2倍は6銭」として計算するという例があります( ,かけ算の式と言葉の順序 メモ - 木村(1936)).
,かけ算の式と言葉の順序 メモ - 木村(1936)).
現在,どういう書き方なのかは…事例 - 「バツ」から学ぶことをご覧ください.
id:snocchy ちゃんと読んでないけど、「5が3つ」と「3が5つ」では意味が違うという主張はずれてるような…。「5が3つ」を「3つの5」と書いちゃ駄目なの?って話じゃないのか
日本の算数では,
- 5が3つは,5×3
- 3が5つは,3×5
- 3つの5は,5×3
ではないかと思います.
id:mamezou_plus2 先に器の数を想起するか、器に乗った物の数が何戸分あるかの違い。個々の捉え方の問題で、このレベルで書き方を強制しても意味が無い。数式と概念はイコールじゃないし子供の自由な捉え方を阻害してはいけない。
「先に器の数を想起するか、器に乗った物の数が何戸分あるかの違い」は,Vergnaudによる,次の図式が対応します.

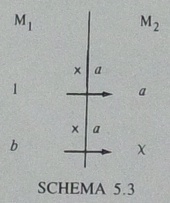
これらの意味は,次のステップをご覧ください.本で確認したければ,『算数・数学科重要用語300の基礎知識』をどうぞ.
id:SUM そういう教え方をした場合と「意味も同じ」って教え方をした場合の教育効果の比較試験の結果を教えてもらって有意に差があったらそっちを支持するよ私は的な感じ。
学術的には,布川2010に書かれている「2年生の導入時では,被乗数と乗数を明確に区別して扱っている」で確定だと思っています.
なので,「意味も同じ」とするほうが教育上いいんだと思う側が,良いというエビデンスを出す責任があります.
なお,量的研究のみで,指導法などの良さを示すのには限界があることも,『数学教育学研究ハンドブック』にて指摘されていますので,ご確認をお願いします.「それは日本ローカルだ」というご意見でしたら,世界的な評価は"The Teaching Gap"*1からお確かめください.
id:research_py 文献が古いんだけど。
- 学術的には,布川2010
- 教師向けなら,『365日の算数学習指導案 1・2年編』と『小二教育技術 2012年11月号』
もっと新しい文献があれば,お知らせください.この機会に,情報を持ち寄りましょう!
id:knjname スーパーでレジ入力している時同じ商品があったら個数を押してからスキャンするんだけど、掛け算にうるさい人はそれも修正させるの?最初にスキャンしてから個数を入力するようにしろとか。生産性ってわかる?
レジ打ちしたことないのですが,そういう挙動を目にします.
その一方で,昨年ギリシャで,「25セント」「単価」「10」「個数」の順に打っているのを見かけました.
先月,レシートのまとめをしたのですが,レジの話はずいぶんと,機械依存ではないかと思います.
ツイートから
当ブログではこれまで,2〜3日分を一気にリリースしてきました.
4日分を一気にというのは,今回が初めてです.
2月5日は何か別トピック(なければ親馬鹿)を書いて,6日からまた何日分か連続で,5×3カテゴリの情報公開をする予定です.
本日の記事と合わせて,日付はお気になさいませんように.
(リリース:Fri Feb 01 21:55:16 JST 2013ごろ)
*1:ただし,この本の中には「かけ算の順序」関連は一切出てきません.教育法や教師モデル,教員間のネットワークについて,日本の特長が挙げられています.
